Любое комплексное число (кроме нуля) 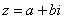можно записать в тригонометрической форме:
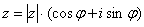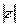, где – это модуль комплексного числа, а 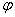– аргумент комплексного числа. Изобразим на комплексной плоскости число 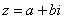. Для определённости и простоты объяснений расположим его в первой координатной четверти, т.е. считаем, что :

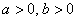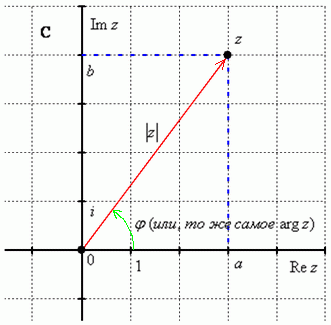
Напоминаю, модулем комплексного числа 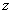называется расстояние от начала координат до соответствующей точки комплексной плоскости.

Модуль комплексного числа 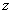стандартно обозначают: 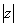или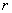

По теореме Пифагора легко вывести формулу для нахождения модуля комплексного числа: 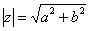. Данная формула справедлива для любых значений «а» и «бэ».

Аргументом комплексного числа 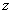называется угол 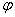между положительной полуосью действительной оси 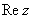и радиус-вектором, проведенным из начала координат к соответствующей точке. Аргумент не определён для единственного числа: .

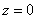Аргумент комплексного числа 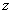стандартно обозначают: 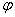или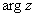

Из геометрических соображений получается следующая формула для нахождения аргумента:
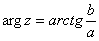. Внимание! Данная формула работает только в правой полуплоскости! Если комплексное число располагается не в 1-ой и не 4-ой координатной четверти, то формула будет немного другой. Эти случаи мы тоже разберем.

Но сначала рассмотрим простейшие примеры, когда комплексные числа располагаются на координатных осях.

Пример 1

Представить в тригонометрической форме комплексные числа: , , , .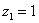

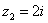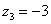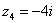На самом деле задание устное. Для наглядности перепишу тригонометрическую форму комплексного числа: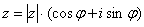

Запомним намертво, модуль – длина (которая всегда неотрицательна), аргумент – угол.

1) Представим в тригонометрической форме число 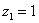. Найдем его модуль и аргумент. Очевидно, что 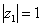. Формальный расчет по формуле: .
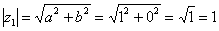Очевидно, что 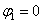(число лежит непосредственно на действительной положительной полуоси). Таким образом, число в тригонометрической форме: .

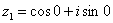Ясно, как день, обратное проверочное действие: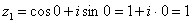

2) Представим в тригонометрической форме число 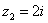. Найдем его модуль и аргумент. Очевидно, что 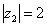. Формальный расчет по формуле: .
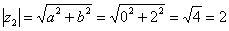Очевидно, что 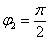(или 90 градусов). На чертеже угол обозначен красным цветом. Таким образом, число в тригонометрической форме: .

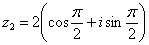Используя таблицу значений тригонометрических функций, легко обратно получить алгебраическую форму числа (заодно выполнив проверку):

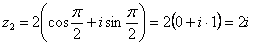
3) Представим в тригонометрической форме число 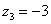. Найдем его модуль и аргумент. Очевидно, что 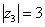. Формальный расчет по формуле: .
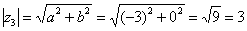Очевидно, что 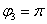(или 180 градусов). На чертеже угол обозначен синим цветом. Таким образом, число в тригонометрической форме: .

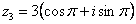Проверка: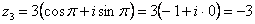

4) И четвёртый интересный случай. Представим в тригонометрической форме число 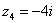. Найдем его модуль и аргумент. Очевидно, что 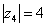. Формальный расчет по формуле: .

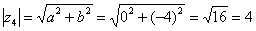Аргумент можно записать двумя способами: Первый способ: 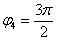(270 градусов), и, соответственно: 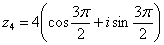. Проверка: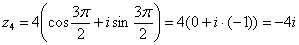

18.2 ДЕЙСТВИЯ С КОМПЛЕКСНЫМИ ЧИСЛАМИ В ТРИГОНОМЕТРИЧЕСКОЙ ФОРМЕ

Частное комплексных чисел