КОНСПЕКТ 17
17.1 СОПРЯЖЕННЫЕ КОМПЛЕКСНЫЕ ЧИСЛА
При решении квадратных уравнений часто используется сокращенная запись, оба корня записывают в одну строчку под «одной гребёнкой»: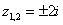 
.
Такие корни также называют сопряженными комплексными корнями. Итак сопряженные комплексные числа – числа, которые отличаются ТОЛЬКО ОДНИМ ЗНАКОМ ПЕРЕД МНИМОЙ ЧАСТЬЮ.
17.2 МОДУЛЬ КОМПЛЕКСНОГО ЧИСЛА
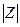– это модуль комплексного числа
Изобразим на комплексной плоскости число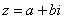 
. Для определённости и простоты объяснений расположим его в первой координатной четверти, т.е. считаем, что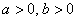 
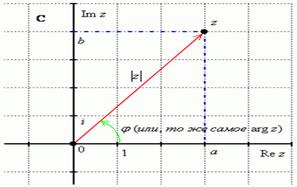
Модулем комплексного числа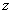 
называется расстояние от начала координат до соответствующей точки комплексной плоскости. Попросту говоря, модуль – это длина радиус-вектора, который на чертеже обозначен ОZ и выделен красным цветом.
Модуль комплексного числа 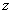стандартно обозначают: 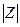или r
По теореме Пифагора легко вывести формулу для нахождения модуля комплексного числа: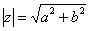 
. Данная формула справедлива для любых значений «а» и «бэ».
Пример 1
Вычислить модуль комплексного числа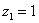 
. Очевидно, что 
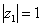. Формальный расчет по формуле: 
.
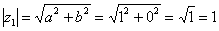Пример 2
Вычислить модуль комплексного числа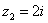 
. Очевидно, что 
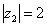. Формальный расчет по формуле: 
.
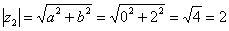Пример 3
Вычислить модуль комплексного числа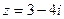 
. 
ПРАКТИКУМ 17
ЗАДАНИЕ N 1
Тема: Сопряженные комплексные числа
Комплексное число, сопряженное числу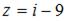 
, равно …
Решение:
Напоминаем, что два комплексных числа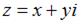 
и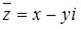 
, отличающиеся только знаком мнимой части, называются сопряженными.
Поэтому, комплексное число, сопряженное данному числу имеет вид - 9 - i
ЗАДАНИЕ N 2
Тема: Сопряженные комплексные числа
Комплексное число, сопряженное числу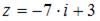 
, равно …
Решение:
Напоминаем, что два комплексных числа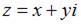 
и 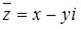, отличающиеся только знаком мнимой части, называются сопряженными
Поэтому, комплексное число, сопряженное данному числу имеет вид 7 i+3
ЗАДАНИЕ N 3
Тема: Модуль комплексного числа
Модуль комплексного числа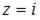 
равен …
Решение:
Напоминаем, что модуль комплексного числа вычисляется по формуле 
, где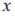 
действительная, а 
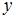мнимая часть комплексного числа.
Тогда 
ЗАДАНИЕ N 4
Тема: Модуль комплексного числа
Модуль комплексного числа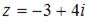 
равен …
Решение:
Напоминаем, что модуль комплексного числа вычисляется по формуле 
, где 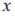действительная, а 
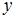мнимая часть комплексного числа.
Тогда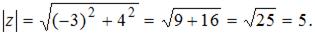 
ЗАДАНИЕ N 5
Тема: Модуль комплексного числа
Модуль комплексного числа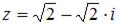 
равен …
Решение:
Модуль комплексного числа вычисляется по формуле 
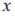, где – действительная, а 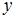– мнимая часть комплексного числа.
Тогда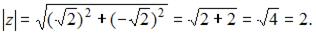 
ЗАДАНИЕ N 6
Тема: Модуль комплексного числа
Модуль комплексного числа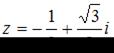 
равен …
Решение:
Модуль комплексного числа вычисляется по формуле 
, где 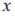– действительная, а 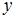– мнимая часть комплексного числа.
Тогда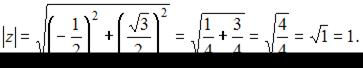 
ЗАДАНИЕ N 7
Тема: Модуль комплексного числа
Модуль комплексного числа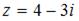 
равен …
Решение:
Напоминаем, что модуль комплексного числа вычисляется по формуле 
, где 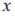действительная, а 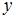мнимая часть комплексного числа.
Тогда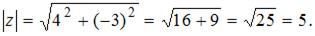 
ЗАДАНИЕ N 8
Тема: Модуль комплексного числа
Модуль комплексного числа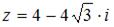 
равен …
Решение:
Модуль комплексного числа вычисляется по формуле 
, где 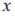– действительная, а 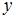– мнимая часть комплексного числа.
Тогда 
САМОСТОЯТЕЛЬНАЯ РАБОТА 17
ЗАДАНИЕ N 1
Тема: Сопряженные комплексные числа
Комплексное число, сопряженное числу 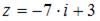, равно …
ЗАДАНИЕ N 2
Тема: Сопряженные комплексные числа
Комплексное число, сопряженное числу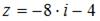 
, равно …
ЗАДАНИЕ N 3
Тема: Сопряженные комплексные числа
Комплексное число, сопряженное числу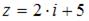 
, равно …
ЗАДАНИЕ N 4
Тема: Сопряженные комплексные числа
Комплексное число, сопряженное числу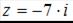 
, равно …
ЗАДАНИЕ N 5
Тема: Сопряженные комплексные числа
Комплексное число, сопряженное числу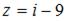 
, равно …
ЗАДАНИЕ N 6
Тема: Модуль комплексного числа
Модуль комплексного числа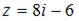 
равен …
ЗАДАНИЕ N 7
Тема: Модуль комплексного числа
Модуль комплексного числа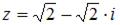 
равен …
ЗАДАНИЕ N 8
Тема: Модуль комплексного числа
Модуль комплексного числа 
равен …
ЗАДАНИЕ N 9
Тема: Модуль комплексного числа
Модуль комплексного числа 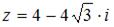равен …
ТЕМА 18 ТРИГОНОМЕТРИЧЕСКАЯ ФОРМА КОМПЛЕКСНОГО ЧИСЛА. ДЕЙСТВИЯ НАД КОМПЛЕКСНЫМИ ЧИСЛАМИ В ТРИГОНОМЕТРИЧЕСКОЙ ФОРМЕ
КОНСПЕКТ 18.
Дата: 2019-07-31, просмотров: 179.
