2) Вы должны понимать и сразу решать простейшие пределы, такие как 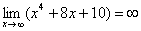 ,
, 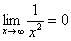 ,
, 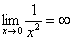 и т.д.
и т.д.
ПРАКТИКУМ 19
ЗАДАНИЕ N 1
Тема: Способы задания числовых последовательностей
Общий член последовательности выражается формулой 
Тогда 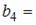 …
…
Решение:
В формулу общего члена вместо n подставим число 4. Получим: 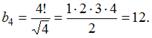
ЗАДАНИЕ N 2
Тема: Способы задания числовых последовательностей
Общий член последовательности выражается формулой 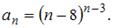
Тогда 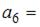 …
…
Решение:
В формулу общего члена вместо n подставим число 6. Получим: 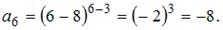
ЗАДАНИЕ N 3
Тема: Способы задания числовых последовательностей
Общий член последовательности выражается формулой 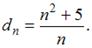
Тогда 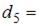 …
…
Решение:
В формулу общего члена вместо n подставим число 5. Получим: 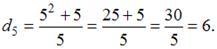
ЗАДАНИЕ N 4
Тема: Предел функции в точке
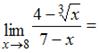 …
…
Решение:
Напоминаем, что для вычисления предела многочлена при 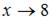 достаточно вместо переменной
достаточно вместо переменной 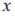 поставить значение
поставить значение 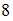 , к которому она стремится, и выполнить соответствующие действия:
, к которому она стремится, и выполнить соответствующие действия:
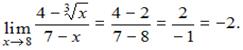
ЗАДАНИЕ N 5
Тема: Предел функции в точке
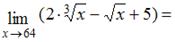 …
…
Решение:
Напоминаем, что для вычисления предела многочлена при 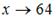 достаточно вместо переменной
достаточно вместо переменной 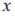 поставить значение
поставить значение 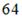 , к которому она стремится, и выполнить соответствующие действия:
, к которому она стремится, и выполнить соответствующие действия:
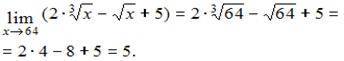
САМОСТОЯТЕЛЬНАЯ РАБОТА 19
ЗАДАНИЕ N 1
Тема: Способы задания числовых последовательностей
Общий член последовательности выражается формулой 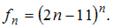
Тогда 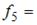 …
…
ЗАДАНИЕ N 2
Тема: Способы задания числовых последовательностей
Общий член последовательности выражается формулой 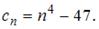
Тогда 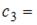 …
…
ЗАДАНИЕ N 3
Тема: Способы задания числовых последовательностей
Общий член последовательности выражается формулой 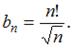
Тогда 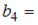 …
…
ЗАДАНИЕ N 4
Тема: Способы задания числовых последовательностей
Общий член последовательности выражается формулой 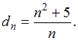
Тогда 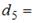 …
…
ЗАДАНИЕ N 5
Тема: Способы задания числовых последовательностей
Общий член последовательности выражается формулой 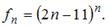
Тогда 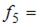 …
…
ЗАДАНИЕ N 6
Тема: Способы задания числовых последовательностей
Общий член последовательности выражается формулой 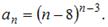
Тогда 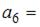 …
…
ЗАДАНИЕ N 7
Тема: Предел функции в точке
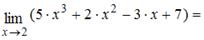 …
…
ЗАДАНИЕ N 8
Тема: Предел функции в точке
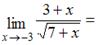 …
…
ЗАДАНИЕ N 9
Тема: Предел функции в точке
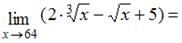 …
…
ЗАДАНИЕ N 10
Тема: Предел функции в точке
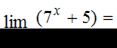 …
…
ТЕМА 20 РАСКРЫТИЕ НЕОПРЕДЕЛЕННОСТИ ВИДА «НОЛЬ НА НОЛЬ». РАСКРЫТИЕ НЕОПРЕДЕЛЕННОСТИ «БЕСКОНЕЧНОСТЬ НА БЕСКОНЕЧНОСТЬ»
КОНСПЕКТ 20
20.1 РАСКРЫТИЕ НЕОПРЕДЕЛЕННОСТИ ВИДА 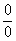
Пример 1
Решить предел 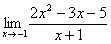
Сначала попробуем подставить -1 в дробь:
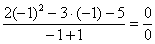
В данном случае получена так называемая неопределенность 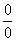 .
.
Общее правило: если в числителе и знаменателе находятся многочлены, и имеется неопределенности вида 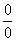 , то для ее раскрытия нужно разложить числитель и знаменатель на множители.
, то для ее раскрытия нужно разложить числитель и знаменатель на множители.
Для этого чаще всего нужно решить квадратное уравнение и (или) использовать формулы сокращенного умножения.
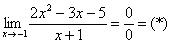
Разложим числитель на множители.
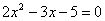
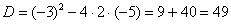
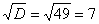
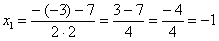
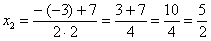
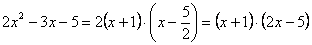
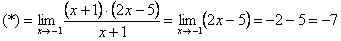
Пример 2
Вычислить предел 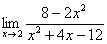
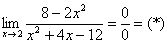
Разложим числитель и знаменатель на множители.
Числитель: 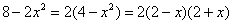
Знаменатель:
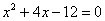
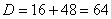
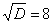
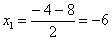 ,
, 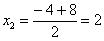
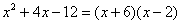
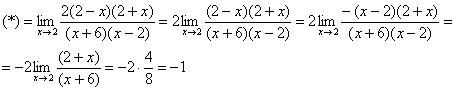
Дата: 2019-07-31, просмотров: 294.