КОНСПЕКТ 14
14.1 ОСНОВНЫЕ ФОРМУЛЫ КОМБИНАТОРИКИ
a) перестановки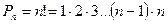 
b) размещения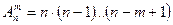 
c) сочетания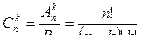 
14.2 КЛАССИЧЕСКОЕ ОПРЕДЕЛЕНИЕ ВЕРОЯТНОСТИ
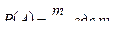- число благоприятствующих событию A исходов, n – число всех элементарных равновозможных исходов.
Теорема сложения вероятностей несовместных событий:
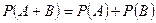
Теорема сложения вероятностей совместных событий:
Теорема умножения вероятностей независимых событий:
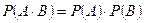
Теорема умножения вероятностей зависимых событий:
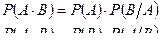
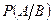- условная вероятность события A при условии, что произошло событие B.
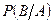- условная вероятность события B при условии, что произошло событие A.
14.3 СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
Закон распределения дискретной случайной величины
 xi
| x1
| x2
| …… | xn
|
| pi | p1 | p2 | …… | pn |
Сумма вероятностей всегда равна 1.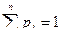 
Функция распределения случайной величины
Функция распределения случайной величины X определяется по формуле
F( x) = P ( X < x). Это неубывающая функция, принимающая значения от 0 до 1.
Математическое ожидание случайной величины
1) Для дискретной случайной величины X, заданной рядом распределения:
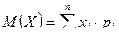
1) Для непрерывной случайной величины X, заданной плотностью распределения:
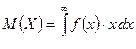
Дисперсия случайной величины
По определению дисперсия – это второй центральный момент:
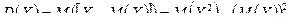
1) Для дискретной случайной величины X, заданной рядом распределения:
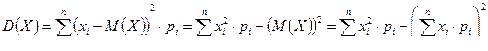
1) Для непрерывности случайной величины X, заданной плотностью распределения:
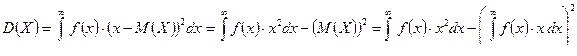
Среднее квадратическое отклонение случайной величины
Распределения случайных величин
Биномиальное распределение (дискретное)
X – количество «успехов» в последовательности из n независимых случайных экспериментов, таких что вероятность «успеха» в каждом из них равна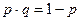 
Закон распределения X имеет вид:
| xk | 0 | 1 | …… | k | …… | n |
| pk | qn |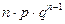 
| 
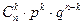
| pn |
Здесь вероятности находятся по формуле Бернулли: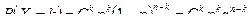 
Характеристики: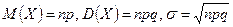 
Примеры многоугольников распределения для n=5 и различных вероятностей:
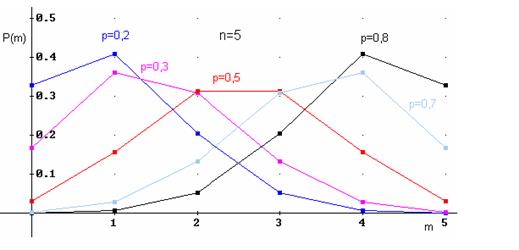
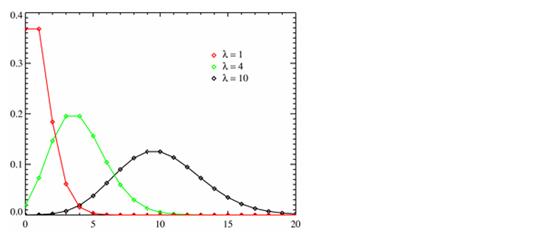
Пуассоновское распределение (дискретное)
Распределение Пуассона моделирует случайную величину, представляющую собой число событий, произошедших за фиксированное время, при условии, что данные события происходят с некоторой фиксированной средней интенсивностью и независимо друг от друга.
При условии p →0, n →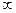 
, np → 
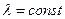закон распределения Пуассона является предельным случаем биномиального закона. Так как при этом вероятность p события A в каждом испытании мала, то закон распределения Пуассона называют часто законом редких явлений.
Ряд распределения:
| xk | 0 | 1 | …… | k | …… |
| pk | e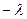 
| 
| …… | 
| …… |
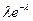
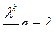
Вероятности вычисляются по формуле Пуассона: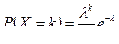 
Числовые характеристики: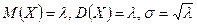 
Разные многоугольники распределения при 
ПРАКТИКУМ 14
ЗАДАНИЕ N 1
Тема: Классическое определение вероятности
Бросают игральную кость. Число очков, меньшее 4, выпадет с вероятностью,
равной …
Решение:
Вероятностью Р(А) события А называется отношение числа благоприятных для А исходов к числу всех равновозможных исходов. По условию задачи число благоприятных исходов, то есть количество выпадений чисел, меньшее 4, равно 3 (выпали числа 1, 2, или 3). Число всех равновозможных исходов равно 6, тогда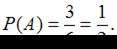 
ЗАДАНИЕ N 2
Тема: Классическое определение вероятности
В урне 10 шаров, имеющих номера: 1, 2, …, 10. Наугад вынутый шар имеет номер, больший 4, с вероятностью, равной …
Решение:
Вероятностью Р(А) события А называется отношение числа благоприятных для А исходов к числу всех равновозможных исходов. По условию задачи число благоприятных исходов, то есть количество выпадений номеров больших 4, равно 6 (выпали номера 5, 6, 7, 8, 9 или 10). Число всех равновозможных исходов равно 10, тогда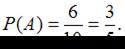 
ЗАДАНИЕ N 3
Тема: Теоремы сложения и умножения вероятностей
Имеются два пакета семян, имеющих всхожесть 
и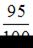 
соответственно.
Вероятность того, что после посадки всех семян из обоих пакетов не взойдет ни одно семя, равна …
Решение:
Пусть событие А означает, что не взойдет ни одно семя из первого пакета, тогда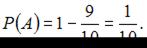 
Событие В означает, что не взойдет ни одно семя из второго пакета, тогда 
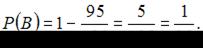События А и В являются независимыми. Тогда вероятность совместного появления двух независимых событий равна произведению вероятностей этих событий: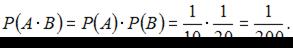 
ЗАДАНИЕ N 4
Тема: Теоремы сложения и умножения вероятностей
Первый спортсмен попадает в мишень с вероятностью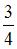 
, а второй – с
вероятностью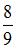 
. Оба спортсмена стреляют одновременно. Вероятность того, что они оба попадут в мишень, равна …
Решение:
Пусть событие А означает, что первый спортсмен попадет в мишень, тогда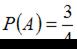 
. Событие В означает, что второй спортсмен попадет в мишень, тогда 
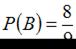. События А и В являются независимыми. Тогда вероятность совместного появления двух независимых событий равна произведению вероятностей этих событий:
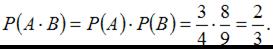
ЗАДАНИЕ N 5
Тема: Элементы комбинаторики
Пин-код пластиковой карты состоит из 6 цифр: 1, 2, 3, 4, 5, 6. Если бы каждая цифра встречалась ровно один раз, то максимальное количество карт с такими кодами было бы равно …
Решение:
Число различных кодов, состоящих из 6 цифр: 1, 2, 3, 4, 5, 6, в которых каждая цифра встречается ровно один раз, равно числу перестановок из шести элементов: 
ЗАДАНИЕ N 6
Тема: Элементы комбинаторики
Пароль состоит из 3 букв слова «код». Каждая буква может встречаться ровно один раз. Тогда максимальное количество возможных паролей равно …
Решение:
Число различных паролей, состоящих из 3 букв слова «код», в которых каждая буква встречается ровно один раз, равно числу перестановок из трех элементов: 
ЗАДАНИЕ N 7
Тема: Элементы комбинаторики
Автомобилю может быть присвоен номер, состоящий из 4 цифр: 1, 3, 5, 7, 9. Цифры в номере повторяться не могут. Тогда максимальное количество автомобилей, которым могут быть присвоены такие номера, равно …
Решение:
Число различных номеров из 5 цифр: 1, 3, 5, 7, 9, в которых каждая цифра встречается ровно один раз, равно числу перестановок из пяти элементов: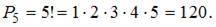 
ЗАДАНИЕ N 8
Тема: Математическое ожидание дискретной случайной величины
Математическое ожидание М(Х) случайной величины, имеющей закон распределения вероятностей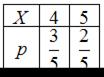 
, равно …
Решение:
По определению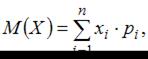 
где 
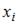– значение дискретной случайной величины; а 
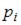– вероятность, с которой дискретная случайная величина принимает значение 
Тогда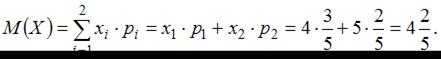 
ЗАДАНИЕ N 9
Тема: Математическое ожидание дискретной случайной величины
Математическое ожидание М(Х) случайной величины, имеющей закон распределения вероятностей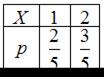 
, равно …
Решение:
Воспользуемся формулой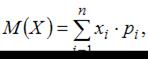 
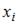где – значение дискретной случайной величины; а 
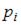– вероятность, с которой дискретная случайная величина принимает значение 
.
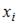Тогда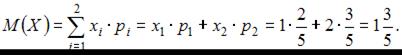 
САМОСТОЯТЕЛЬНАЯ РАБОТА 14
ЗАДАНИЕ N 1
Тема: Классическое определение вероятности
Бросают игральную кость. Число очков, большее 3, выпадет с вероятностью,
равной …
ЗАДАНИЕ N 2
Тема: Классическое определение вероятности
Бросают игральную кость. Число очков, большее 4, выпадет с вероятностью,
равной …
ЗАДАНИЕ N 3
Тема: Классическое определение вероятности
Бросают игральную кость. Число очков, большее 4, выпадет с вероятностью,
равной …
ЗАДАНИЕ N 4
Тема: Классическое определение вероятности
В урне 10 шаров, имеющих номера: 1, 2, …, 10. Наугад вынутый шар имеет номер, меньший 4 с вероятностью, равной …
ЗАДАНИЕ N 5
Тема: Теоремы сложения и умножения вероятностей
Первый спортсмен попадает в мишень с вероятностью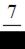 
, а второй – с
вероятностью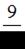 
. Оба спортсмена стреляют одновременно. Вероятность того, что они оба попадут в мишень, равна …
ЗАДАНИЕ N 6
Тема: Теоремы сложения и умножения вероятностей
Имеются два пакета семян, имеющих всхожесть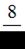 
и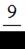 
соответственно.
Вероятность того, что после посадки всех семян из обоих пакетов взойдут все семена, равна …
ЗАДАНИЕ N 7
Тема: Теоремы сложения и умножения вероятностей
В первой урне 2 белых и 3 черных шара, во второй − 4 белых и 6 черных шаров. Из каждой урны вынули по одному шару. Вероятность того, что оба вынутых шара будут белыми, равна …
ЗАДАНИЕ N 8
Тема: Теоремы сложения и умножения вероятностей
В первой урне 7 белых и 3 черных шара, во второй − 6 белых и 3 черных шара. Из каждой урны вынули по одному шару. Вероятность того, что оба вынутых шара будут черными, равна …
ЗАДАНИЕ N 9
Тема: Теоремы сложения и умножения вероятностей
Имеются два ящика с деталями. Вероятность вынуть бракованную деталь из первого ящика равна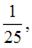 
а из второго − 
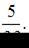Наугад вынимают по одной детали из каждого ящика. Вероятность того, что обе детали окажутся бракованными, равна …
ЗАДАНИЕ N 10
Тема: Теоремы сложения и умножения вероятностей
В первой шкатулке находится 18 монет одинакового достоинства. Известно, что две из них являются фальшивыми. Во второй шкатулке 10 монет, из которых 3 монета фальшивая. Из каждой шкатулки наугад берут по одной монете. Вероятность того, что обе монеты окажутся фальшивыми, равна …
ЗАДАНИЕ N 11
Тема: Математическое ожидание дискретной случайной величины
Математическое ожидание М(Х) случайной величины, имеющей закон распределения вероятностей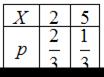 
, равно …
ЗАДАНИЕ N 12
Тема: Математическое ожидание дискретной случайной величины
Математическое ожидание М(Х) случайной величины, имеющей закон распределения вероятностей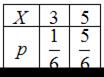 
, равно …
ЗАДАНИЕ N 13
Тема: Математическое ожидание дискретной случайной величины
Математическое ожидание М(Х) случайной величины, имеющей закон распределения вероятностей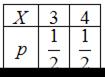 
, равно …
ЗАДАНИЕ N 14
Тема: Элементы комбинаторики
Пин−код пластиковой карты состоит из 5 цифр: 1, 2, 3, 4, 5. Если бы каждая цифра встречалась ровно один раз, то максимальное количество карт с такими кодами было бы равно …
ЗАДАНИЕ N 15
Тема: Элементы комбинаторики
Пароль состоит из 6 букв: a, b, c, d, i, j. Каждая буква встречается ровно один раз. Тогда максимальное количество возможных паролей равно …
ЗАДАНИЕ N 16
Тема: Элементы комбинаторики
Код замка состоит из 4 цифр: 1, 3, 5, 7. Каждая цифра встречается ровно один раз. Тогда максимальное количество замков с такими кодами равно …
ЗАДАНИЕ N 17
Тема: Элементы комбинаторики
Автомобилю может быть присвоен номер, состоящий из 4 цифр: 1, 3, 5, 7, 9. Цифры в номере повторяться не могут. Тогда максимальное количество автомобилей, которым могут быть присвоены такие номера, равно …
Дата: 2019-07-31, просмотров: 180.
