КОНСПЕКТ 2
2.1 ОПРЕДЕЛИТЕЛИ ВТОРОГО ПОРЯДКА
Определителем второго порядка (соответствующим данной матрице
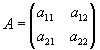 ) называется число
) называется число 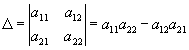
Пример1: Вычислим определитель матрицы
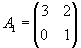
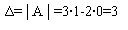
Пример 2. Вычислить определители второго порядка:
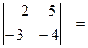 2(-4) - 5(-3) = -8 + 15 = 7
2(-4) - 5(-3) = -8 + 15 = 7
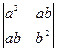 =
= 
2.2 ОПРЕДЕЛИТЕЛИ ТРЕТЬЕГО ПОРЯДКА
Пусть дана квадратная матрица третьего порядка:
А = 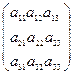
Определителем (или детерминантом) третьего порядка, соответствующим данной матрице, называют число 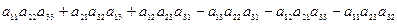
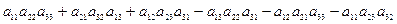 det A =
det A = 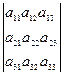 =
=
Пример 3
Первый способ решения:
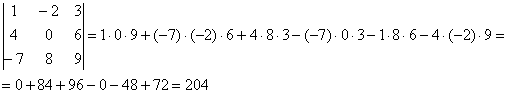
Формула длинная и допустить ошибку по невнимательности проще простого. Как избежать досадных промахов? Для этого придуман второй способ вычисления определителя, который фактически совпадает с первым. Называется он способом Саррюса или способом «параллельных полосок».
Суть состоит в том, что справа от определителя приписывают первый и второй столбец и аккуратно карандашом проводят линии:
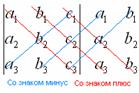
Множители, находящиеся на «красных» диагоналях входят в формулу со знаком «плюс».
Множители, находящиеся на «синих» диагоналях входят в формулу со знаком минус:
Пример 3
Второй способ решения:
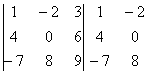
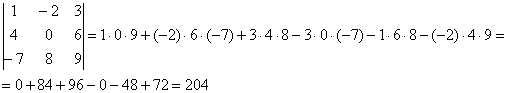
Сравните два решения. Нетрудно заметить, что это ОДНО И ТО ЖЕ, просто во втором случае немного переставлены множители формулы, и, самое главное, вероятность допустить ошибку значительно меньше.
Пример 4
Вычислить определитель третьего порядка:
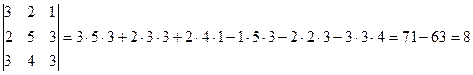
Пример 5
Вычислить определитель третьего порядка
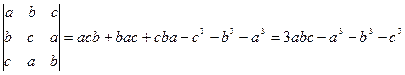
ПРАКТИКУМ 2
ЗАДАНИЕ N 1
Тема: Определители второго порядка
Если определитель второго порядка 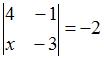 , то
, то 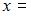 …
…
Решение:
Так как определитель второго порядка равен числу, которое получают по правилу:
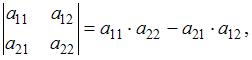 то
то
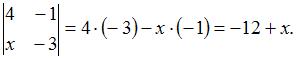
По условию 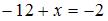 , тогда
, тогда 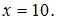
ЗАДАНИЕ N 2
Тема: Определители второго порядка
Если определитель второго порядка
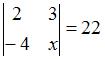 , то
, то 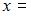 …
…
Решение:
Напоминаем, что определитель второго порядка равен числу,
которое получают по правилу:
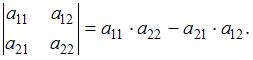
В нашем случае имеем
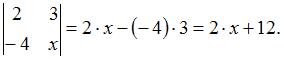
По условию 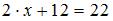 , тогда
, тогда 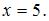
ЗАДАНИЕ N 3
Тема: Определители второго порядка
Если определитель второго порядка
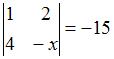 , то
, то 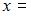 …
…
Решение:
Так как определитель второго порядка равен числу, которое получают по правилу:
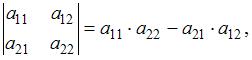 то
то
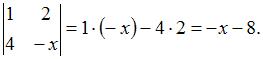
По условию 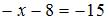 , тогда
, тогда 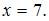
ЗАДАНИЕ N 4
Тема: Определители второго порядка
Если определитель второго порядка 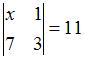 , то
, то 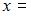 …
…
Решение:
Напоминаем, что определитель второго порядка равен числу,
которое получают по правилу:
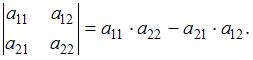
В нашем случае имеем
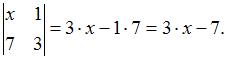
По условию 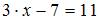 , тогда
, тогда 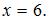
ЗАДАНИЕ N 5
Тема: Определители третьего порядка
Значение определителя третьего порядка можно вычислить, используя
«правило треугольников», которое схематически указано на рисунках.
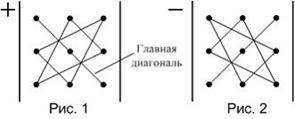
Тогда определитель  равен …
равен …
Решение:
Определитель третьего порядка равен сумме шести слагаемых, из которых три берутся со знаком «+» и три – со знаком «−». Правило вычисления слагаемых со знаком «+» схематически указано на рис. 1. Одно из слагаемых равно произведению элементов определителя, лежащих на главной диагонали. Каждое из двух других находится как произведение элементов, лежащих на параллели к этой диагонали, с добавлением третьего множителя из противоположного угла определителя. Слагаемые со знаком «−» получаются таким же образом, но относительно второй диагонали (рис. 2).
Тогда 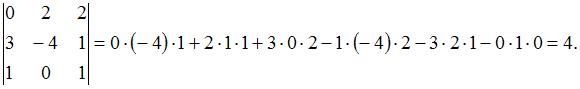
ЗАДАНИЕ N 6
Тема: Определители третьего порядка
Значение определителя третьего порядка можно вычислить, используя
«правило треугольников», которое схематически указано на рисунках.
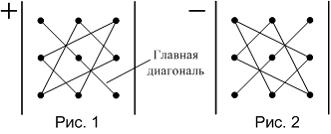
Тогда определитель  равен …
равен …
Решение:
Определитель третьего порядка равен сумме шести слагаемых, из которых три берутся со знаком «+» и три – со знаком «−». Правило вычисления слагаемых со знаком «+» схематически указано на рис. 1. Одно из слагаемых равно произведению элементов определителя, лежащих на главной диагонали. Каждое из двух других находится как произведение элементов, лежащих на параллели к этой диагонали, с добавлением третьего множителя из противоположного угла определителя. Слагаемые со знаком «−» получаются таким же образом, но относительно второй диагонали (рис. 2).
Тогда 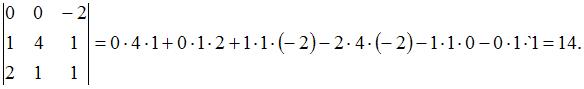
САМОСТОЯТЕЛЬНАЯ РАБОТА 2
ЗАДАНИЕ N 1
Тема: Определители второго порядка
Если определитель второго порядка 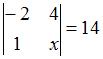 , то
, то 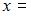 …
…
ЗАДАНИЕ N 2
Тема: Определители второго порядка
Если определитель второго порядка 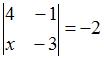 , то
, то 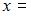 …
…
ЗАДАНИЕ N 3
Тема: Определители второго порядка
Если определитель второго порядка 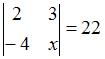 , то
, то  …
…
ЗАДАНИЕ N 4
Тема: Определители третьего порядка
Значение определителя третьего порядка можно вычислить, используя
«правило треугольников», которое схематически указано на рисунках.
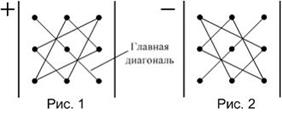
Тогда определитель  равен …
равен …
ЗАДАНИЕ N 5
Тема: Определители третьего порядка
Значение определителя третьего порядка можно вычислить, используя
«правило треугольников», которое схематически указано на рисунках.
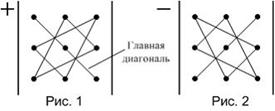
Тогда определитель  равен …
равен …
ЗАДАНИЕ N 6
Тема: Определители третьего порядка
Значение определителя третьего порядка можно вычислить, используя
«правило треугольников», которое схематически указано на рисунках.
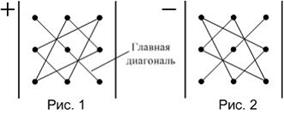
Тогда определитель  равен …
равен …
ЗАДАНИЕ N 7
Тема: Определители третьего порядка
Значение определителя третьего порядка можно вычислить, используя
«правило треугольников», которое схематически указано на рисунках.
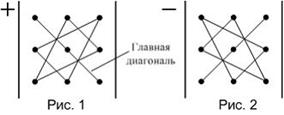
Тогда определитель  равен …
равен …
ЗАДАНИЕ N 8
Тема: Определители третьего порядка
Значение определителя третьего порядка можно вычислить, используя
«правило треугольников», которое схематически указано на рисунках.
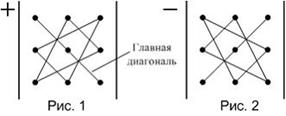
Тогда определитель  равен …
равен …
Дата: 2019-07-31, просмотров: 332.