Эквивалентирование широко применяется в расчетах режимов сложных электроэнергетических систем. Так, рассматривая режимы работы отдельной ЭЭС, все соседние энергосистемы представляем их эквивалентами, полученными на основании так называемых критериев эквивалентности. Число таких критериев и их содержание зависят от задачи, применительно к которой выполняется эквивалентирование.

Рассмотрим ЭЭС, состоящую из двух подсистем: подсистемы I, которая не подлежит преобразованию, и подсистемы II, которую следует преобразовать в эквивалент (рис. 3.12, а).

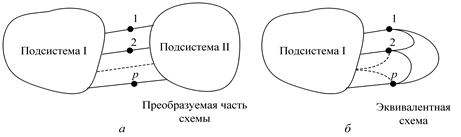
Рис. 3.12. Условное изображение ЭЭС с эквивалентируемой частью: а – до эквивалентирования; б – после эквивалентирования

Узлы, в которых соединяются две подсистемы, называются узлами примыкания, а ветви, подходящие к ним со стороны сохраняемой части схемы, – ветвями примыкания. После преобразования подсистемы II в ней могут сохраниться некоторые узлы, имеющие принципиальное значение для режимов системы, или не сохраниться ни одного узла, как на рис. 3.12, б, и вся схема эквивалента представляет собой многоугольник, построенный на узлах примыкания 1, 2,…, p. Следует отметить, что эквивалент имеет также поперечные ветви на нейтральную плоскость системы как пассивные – проводимости, так и активные – задающие мощности нагрузки и генерации (на рис. 3.12 не показаны).

Рассчитанные напряжения в узлах примыкания эквивалента должны быть равны в исходной схеме и после ее преобразования.

Потоки мощности в ветвях примыкания эквивалента должны быть равны в исходной схеме и после ее преобразования.

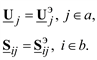(3.53)

где a – множество номеров узлов примыкания;

b – множество номеров узлов в непреобразуемой части сети, имеющих смежную ветвь с узлами примыкания.

Добиться выполнения критериев эквивалентности можно, как правило, для какого-то одного режима работы электрической системы.

Изменение режима требует и изменения (корректировки) эквивалента.

Рассмотрим пример эквивалентирования части электрической схемы сети (рис. 3.13, а). В этом примере: множество номеров узлов примыкания (a) = {4, 7, 11}; множество номеров узлов из неэквивалентируемой части схемы, смежных с узлами примыкания (б) = {3, 6, 10}.

Исключаемые узлы: {12, 13, 14, 15, 16}.

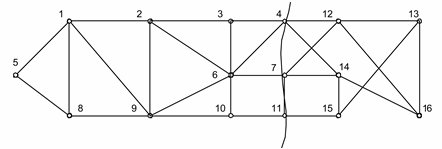
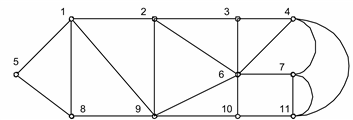
Рис. 3.13. Граф сети с эквивалентируемой частью: а – до эквивалентирования; б – после эквивалентирования

В данном примере в эквиваленте не сохранено ни одного узла и граф эквивалента представляет собой многоугольник, опирающийся вершинами на узлы примыкания (рис. 3.14).

По сути – это последовательно-параллельные преобразования, а также преобразования звезды в многоугольник и обратно. Формализуется исключением переменных методом Гаусса.

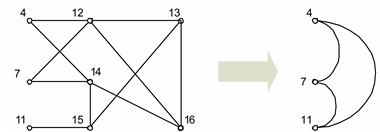
Рис. 3.14. Эквивалентирование схемы в многоугольник

При построении модели эквивалента, адекватно представляющего преобразованную часть электрической системы для множества режимов, требуется учет нелинейности уравнений установившегося режима. В этом случае, а также в случаях эквивалентирования посредством расчета проводимостей нагрузки через номинальное напряжение неизбежна погрешность моделирования.

Минимизация погрешности может быть выполнена поиском минимума некоторой целевой функции:

(3.54)

где y'_j и y''_j^э – компоненты вектора выходных переменных исходной и эквивалентной моделей, которые должны воспроизводится правильно;

R – вектор параметров эквивалентной модели; m – число выходных переменных.

Пример. Для схемы на рис 3.15 выполним исключение узлов номер 4 и 5.

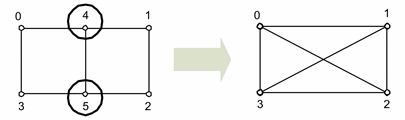
Рис. 3.15. Пример эквивалентирования схемы сети

Разделим на блоки матрицы в линейных уравнениях установившегося режима (3.28) – выделим блоки для сохраняемых и исключаемых узлов.

Обозначим вектор задающих токов сохраняемых узлов: 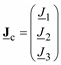, а вектор токов исключаемых узлов 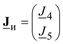. Соответственно и для напряжений .

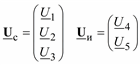Уравнение узловых напряжений для электрической сети

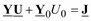
запишется в виде

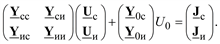
Или в раскрытой форме:

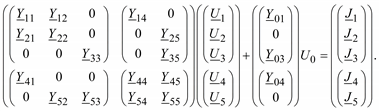
В соответствии с правилом умножения матриц получим

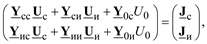
откуда следует система двух матричных уравнений

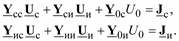
Исключим из этой системы 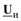, для чего умножим правую и левую части второго уравнения на матрицу и получим

откуда следует

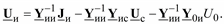
Подставляя теперь полученное выражение в уравнение 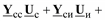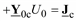, находим

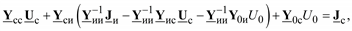
откуда

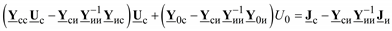
или

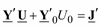
и в развернутой форме

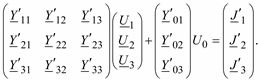
Полученная система уравнений описывает новую схему, где по отношению к исходной отсутствуют два узла 4 и 5. При этом в данном примере изменились все параметры сети и задающие токи узлов.

Эквивалентирование части ЭЭС обычно выполняется не для одного, а для ряда режимов непреобразуемой подсистемы, поэтому удовлетворение критериев эквивалентности должно обеспечить тождественность режима узлов и ветвей примыкания исходной и преобразованной схем не только для исходного, но и для всех других анализируемых режимов.