Часть электрической цепи, рассматриваемая по отношению к двум парам ее выводов, называется четырехполюсником. Ранее здесь использовалось представление четырехполюсником ЛЭП и трансформаторов, однако существует возможность представления в виде четырехполюсника и соединений этих элементов – схем электрических сетей.
Моделирование четырехполюсником удобно применять тогда, когда предметом исследования являются токи (потоки мощности) и напряжения на его выводах, а не токи и напряжения внутри самого четырехполюсника.
По свойству линейности элементов четырехполюсники разделяют на линейные и нелинейные.
Схема замещения (внутренняя схема соединений) четырехполюсника может быть: Г-образная (рис. 3.16, а), Т-образная (рис. 3.16, б), П-образная (рис. 3.16, в), четырехплечая (рис. 3.16, г), П-образная мостовая (рис. 3.16, д), Т-образная мостовая (рис. 3.16, е) и др.
Четырехполюсник называется активным, если он внутри содержит источники электрической энергии, и пассивным, если внутри него нет источников энергии.
Различают четырехполюсники симметричные и несимметричные. Симметричным называют четырехполюсник, когда перемена мест его входа и выхода не изменяет токов и напряжений в цепи, с которой он соединен.
Основной смысл теории четырехполюсников заключается в том, что, пользуясь обобщенными параметрами четырехполюсников, можно находить токи и напряжения на входе и выходе четырехполюсника.
Из множества соединений четырехполюсников в электрических сетях применимы только две: каскадное (рис. 3.16, а) и параллельное (рис. 3.16, б).
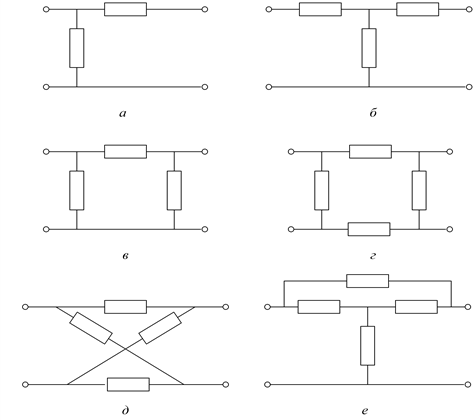
Рис. 3.16. Схемы замещения четырехполюсника
Электрическая сеть, имеющая в общем случае множество узлов и ветвей, может рассматриваться как совокупность четырехполюсников, соединенных по определенной схеме. Отличительной чертой четырехполюсников, моделирующих элементы электрической сети, является наличие у них всех одного общего полюса – нейтральной плоскости, и по сути они могут считаться трехполюсниками. Сложность схемы соединения электрической сети и нелинейность, вносимая нагрузками и генераторами, не позволяют широко использовать четырехполюсники для моделирования электрических сетей. Возможны два принципиально различающихся подхода к использованию четырехполюсников:
· моделирование отдельных элементов или их каскадно-паралельного соединения при отсутствии в них источника энергии или нагрузки, заданных нелинейными математическими моделями;
· приближенное представление части электрической сети при наличии нелинейных моделей генерации или нагрузки в виде эквивалентного четырехполюсника.
Последний подход распространяется на моделирование электрических сетей с помощью многополюсников.
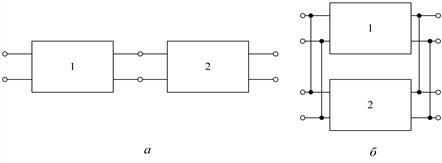
Рис. 3.17. Соединения четырехполюсников: а – каскадное; б – параллельное
Рассмотрим первый подход. Для получения параметров эквивалентного (результирующего) четырехполюсника, составленного из простых четырехполюсников, параметры которых известны, удобно пользоваться матричной формой записи:
 (3.55)
(3.55)
Запись уравнений четырехполюсника (3.54) называется А-формой записи. Другие формы уравнений четырехполюсника могут быть получены из (3.55) выражением в левой части тех или других пар токов и напряжений. Всего возможно шесть форм записи – число сочетаний из четырех по два. Можно выделить еще две формы записи: это Y-форма (3.56) и Z-форма (3.57).
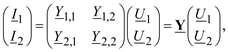 (3.56)
(3.56)
 (3.57)
(3.57)
При каскадном соединении четырехполюсников (рис. 3.17, а) параметры эквивалентного четырехполюсника получаются перемножением матриц коэффициентов четырехполюсников в A-форме (3.55), а при параллельном соединении (рис. 3.17, б) – сложением матриц коэффициентов четырехполюсников в Y-форме (3.56):
 (3.58)
(3.58)
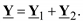 (3.59)
(3.59)
В некоторых случаях для эквивалентирования схем электрических сетей удобно использовать четырехполюсники.
Рассмотрим простые примеры упрощения электрических сетей с помощью четырехполюсников.
Вначале рассмотрим соединение двух элементов: линий электропередач и трансформатора. На рис. 3.18 изображены две схемы с двумя элементами. На первой схеме есть две линии, а на второй линия и трансформатор. В обоих случаях модели сетей с четырехполюсниками имеют их каскадное соединение и эквивалентный четырехполюсник имеет матрицу коэффициентов, вычисляемую по выражению
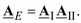 (3.60)
(3.60)
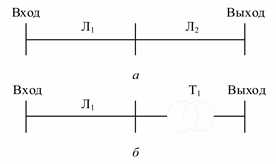

Рис. 3.18. Схема сети с каскадным соединением двух элементов: а – две линии; б – линия и трансформатор; в – каскадное соединение и эквивалентирование четырехполюсников
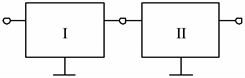
Рис. 3.19. Упрощенное обозначение схем из четырехполюсников в электрических сетях
Далее для простоты вследствие того, что один полюс на входе и на выходе четырехполюсника в схемах электрических систем отождествляют с нейтралью трехфазной системы, четырехполюсники, моделирующие элементы электрических сетей, будем обозначать, как на рис. 3.19.
В схеме с параллельными соединениями элементов будем всегда полагать соединение однотипных элементов: две или более параллельно включенных линии, два или более параллельно включенных трансформатора и т. п. Коэффициенты эквивалентного четырехполюсника в этом случае определяются через матрицы проводимостей уравнений четырехполюсника, записанных в Y-форме (3.56).
Рассмотрим пример схемы, содержащий электрическую нагрузку, заданную мощностью (рис. 3.20).
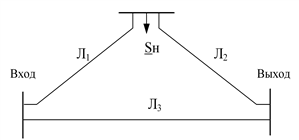
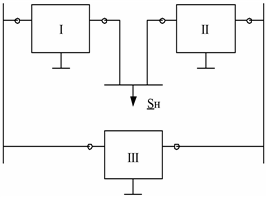
Рис. 3.20. Схема сети с промежуточной нагрузкой: а – схема электрической сети; б – модель сети с четырехполюсниками
Четырехполюсники I и II нельзя считать соединенными каскадно; есть еще один элемент – нагрузка. Рассмотрим этот фрагмент сети отдельно (рис. 3.21).
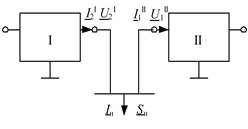
Рис. 3.21. Фрагмент модели сети с промежуточной нагрузкой
Запишем известные соотношения для шин нагрузки:
 (3.61)
(3.61)
Ток нагрузки 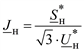 при подстановке его в (3.61) делает эти выражения нелинейными.
при подстановке его в (3.61) делает эти выражения нелинейными.
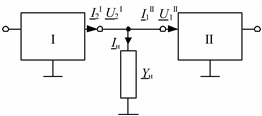
Рис. 3.22. Модель сети с представлением промежуточной нагрузки схемой замещения
Перейдем к модели электрической нагрузки в виде схемы замещения (рис. 3.22)
 (3.62)
(3.62)
и запишем для нее уравнения четырехполюсника:
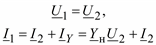 (3.63)
(3.63)
или
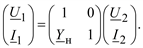 (3.64)
(3.64)
В результате получим каскадное соединение трех четырехполюсников (рис. 3.23).
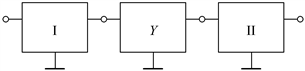
Рис. 3.23. Схема сети с представлением промежуточной нагрузки четырехполюсником
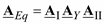 (3.65)
(3.65)
В схеме сети с двумя промежуточными нагрузками аналогично получим (рис. 3.24).
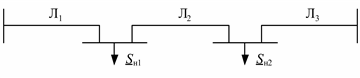

Рис. 3.24. Схема сети из трех линий с промежуточными нагрузками: а – схема сети; б – модель сети с четырехполюсниками
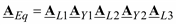 (3.66)
(3.66)
Аналогично нагрузке в схеме электрической сети представляются и другие элементы, включенные в виде шунта (поперечной ветви). К таким элементам относятся компенсирующие устройства и шунтирующие реакторы.
Следует подчеркнуть, что шунтирующие элементы и нагрузки, которые могут быть представлены схемой замещения с линейными элементами (сопротивления и проводимости не зависят от напряжения или тока, протекающего по ним), не вносят погрешности в эквивалентную модель и являются пассивными элементами сети. Нагрузки в электрических сетях, как правило, не могут с достаточной степенью точности моделироваться схемами замещения с постоянными параметрами. По своей сущности нагрузка – это активный элемент сети, хотя не является источником энергии, а ее потребителем. В большинстве случаев нагрузка задается постоянной мощностью или статическими характеристиками, что вносит погрешность при представлении их в виде схем замещения (сопротивления и проводимости зависят от напряжения, приложенного к ним).
Описание при моделировании
Описание объекта моделирования является предметом искусства исследователя. Процесс построения моделей определялся теоретическим багажом исследователя, его неформальными представлениями о цели работы, опытом, экспериментаторским мастерством и интуицией.
Вместе с тем опыт модельных исследований все более сложных объектов убедительно показывал, что качество модели и особенно трудоемкость ее создания решающим образом зависят от того, сколь целесообразно организован процесс изучения объекта, построения, проверки и практического использования его модельного описания. Возникла задача оптимизации процесса моделирования.
Наибольшее развитие методика и практика планирования и осуществления модельных исследований получили в рамках таких направлений, как исследование операций и прикладной системный анализ.
В сложных случаях, когда невозможно составить модели с помощью известных теоретических представлений, получили развитие экспериментальные исследования, названные идентификацией объектов. Применительно к этим исследованиям зародилась и стала стремительно развиваться теория оптимального планирования эксперимента, обеспечивающая получение необходимой экспериментальной информации об объекте при минимальной затрате сил и средств.
В модельном исследовании можно выделить основные этапы: постановку задачи, построение модели, отыскание решения, проверку модели и оценку решения, внедрение модели и контроль ее правильности.
Рассмотрим процесс модельного исследования с помощью его графического представления в форме блок-схемы (рис. 4.1).
Постановка задачи следует за выявлением некоторых противоречий и возникновением проблемы: потребности изменить в лучшую сторону существующее положение вещей в той или иной области.
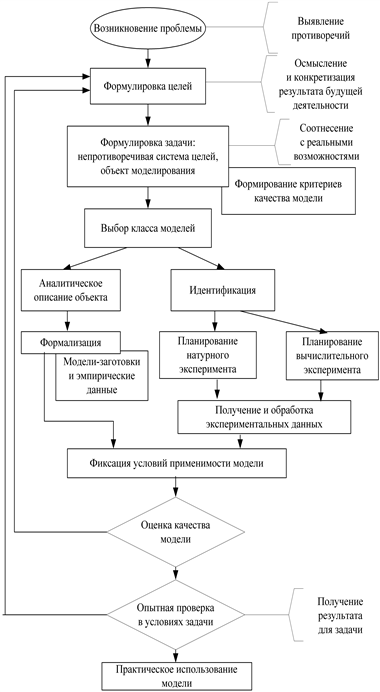
Рис. 4.1. Схема формирования модели
Так, огромное большинство технических и технологических проблем формируется в сфере экономики и экологии – верхних по отношению к технике уровнях системы природа–общество.
Осмысление и конкретизация проблемы приводят к формулировке целей или системы целей как желательного результата будущей деятельности по решению проблемы. Однако поставленная цель, естественно, должна быть соотнесена с реальными возможностями ее достижения или, иными словами, с ресурсами (материальными и другими), которые могут быть использованы для решения данной проблемы. Сопоставление первоначально намеченных целей с ресурсными ограничениями (обычно приводящими к корректировке первых в сторону их сужения) приводит к формулировке задачи исследования, которая помимо непротиворечивой системы целей, учитывающих ресурсные возможности, включает в себя объект моделирования.
Данные о целях исследования, уточненные в формулировке задачи, а также исходная информация об объекте моделирования служат для определения критерия качества создаваемой модели – количественной меры степени ее совершенства. При традиционной постановке задачи исследования критерий обычно не носит формального характера и представляет собой некоторую систему количественных требований, которым должна отвечать будущая модель. В случае вполне формализованной оптимизационной постановки критерий приобретает вид некоторого функционала от переменных и параметров модели, значение которого достигает экстремума при оптимальных ее характеристиках (например, среднеквадратическая погрешность модельных переменных).
Следующим шагом в построении модели является основанный на априорных данных содержательный анализ системы и выбор класса, или точнее, способа формирования модели. Если объект не слишком сложен, достаточно изучен и комплекс подлежащих модельному исследованию свойств и характеристик объекта может быть выявлен на основе теоретических представлений и данных (дополняемых необходимым объемом эмпирической информации), то целесообразно избрать аналитический путь построения модели. Однако на практике часто оказывается, что из-за сложности, слабой изученности объекта или отсутствия соответствующих теоретических разработок (например, применительно к комплексным системам, содержащим технические, информационные, биологические компоненты) этот путь не может быть реализован. Альтернативным является путь идентификации объекта, т. е. экспериментального определения существенных для решаемой задачи свойств и характеристик объекта специально ради построения его модели. Эксперимент, как правило, достаточно сложный и трудоемкий, осуществляется в соответствии со специально разрабатываемым оптимальным планом, данные эксперимента обрабатываются и становятся основой для формализованного описания объекта в виде математической модели вход–выход.
Формализованная модель, построенная теоретическим путем или идентифицированная, оценивается в соответствии с выбранным ранее критерием и либо признается удовлетворительной (принимается), либо отвергается как недостаточно совершенная. В последнем случае возникает необходимость в ее корректировке и итеративном обращении к ранее выполненным этапам.
Решение о принятии модели (в общем случае после i-го итерационного цикла) влечет за собой переход к следующему этапу – опытной проверке непосредственно в условиях той задачи, для решения которой она построена. При этом нередко возникают дополнительные требования (например, связанные с удобством использования модели) и необходимость ее дополнительной корректировки.
Наконец, следует заключительный этап процесса: использование модели по ее прямому назначению – для решения задачи, причем и на этом этапе возможны дальнейшие уточнения и корректировки.
Остановимся на наиболее важных особенностях процесса моделирования в целом.
1. Построение модели представляет собой не однократный акт, а процесс последовательных приближений, в основе которого лежит самообучение исследователя.
2. Процесс моделирования соединяет в себе требования к ясно понимаемому существу решаемой задачи, с одной стороны, и активному владению теорией, математическим аппаратом и методами – с другой стороны. Кроме того, необходимы хорошие знания возможностей вычислительной техники и ее использования.
3. Процесс построения модели является познавательной деятельностью и представляет собой важнейшую составную часть решения задачи в целом.
Аналитический метод
В распоряжении исследователя, решающего на основе моделирования конкретную задачу, сегодня находится огромное множество моделей-«заготовок», которые могут и должны быть использованы. Все эти заготовки получены на основе универсальных законов, таких, как закон сохранения вещества и энергии, начала термодинамики, закон всемирного тяготения. Однако вопрос о том, каким может быть удельный вес теоретической составляющей при построении каждой конкретной модели, целиком определяется требованиями задачи и характером объекта моделирования.
Возможность и рациональность теоретического подхода к моделированию некоторого объекта определяются целым рядом практически не поддающихся формальному анализу факторов, к числу которых относятся:
· степень изученности данного класса объектов и наличие теоретической базы, достаточной для модельного описания объекта в соответствии с требованиями решаемой задачи;
· приемлемость ограничений и допущений, содержащихся в исходных теоретических построениях, применительно к условиям и требованиям решаемой задачи;
· специфические свойства объекта-оригинала (степень сложности и размерность модели, возможность линеаризации, возможность и удобство применения стандартных, например частотных, методов для исследования модели объекта и т. п.);
· возможность и удобство введения в теоретическую модель необходимой дополнительной информации, получаемой опытным путем;
· возможность экспериментального исследования объекта-оригинала.
В основе аналитических моделей, как правило, лежат балансовые соотношения, связывающие входные и выходные переменные. Эти соотношения представляют собой частные проявления законов сохранения вещества и энергии.
Пример 1. В простейшей ЭЭС генератор электрической станции Г (рис. 4.2) работает с мощностью PГ, которая посредством линии электропередачи передается на шины нагрузки, где установлен электродвигатель Д. В такой ЭЭС при неизменной частоте сохраняется баланс активной мощности:
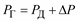 , 41
, 41
где PД – мощность, с которой работает электродвигатель;
DP – потери мощности в линии электропередачи.
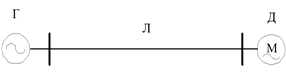
Рис. 4.2. Схема простейшей ЭЭС
Выражение (4.1) является балансовым соотношением, вытекающим из закона сохранения энергии, однако для полного описания модели работы ЭЭС требуются дополнительные экспериментальные данные. К ним относятся характеристики элементов, входящих в ЭЭС: генератора, линии электропередачи и двигателя. Эти элементы являются техническими объектами со своими, свойственными только им, характеристиками. Для получения этих характеристик требуется эксперимент, который проводится непосредственно для этих объектов, либо используются данные экспериментов, выполненные над типичными объектами. К характеристикам электрических объектов относятся, например, статические характеристики генераторов и двигателей по напряжению, а для линии электропередачи – зависимость потерь мощности от напряжения.
Пример 2. При протекании тока по проводу воздушной ЛЭП в соответствии с законом Джоуля–Ленца происходит нагревание проводника:
 42
42
где ΔQ – количество теплоты, выделяемое в проводнике с сопротивлением R при протекании по нему тока I в течение времени Δt.
Если бы не было отвода тепла от проводника, температура проводника возрастала бы неограниченно. Охлаждение проводника происходит лучеиспусканием, конвекцией и теплопередачей из-за наличия теплопроводности окружающей среды.
По условиям сохранения физико-механических характеристик проводов воздушных линий электропередачи температура, до которой могут нагреваться провода, ограничена некоторым значением (как правило 70 ºС). Это связано с ограничением тока, протекающего по проводу Iдоп. Вычислить значение Iдоп позволяет математическое соотношение, выведенное из баланса количества теплоты, создаваемого в отрезке проводника, и отведенного количества теплоты в единицу времени.
Лучеиспускание при θ < 100 ºС незначительно, а теплопроводность окружающего проводник воздуха мала, следовательно, в основном охлаждение идет за счет конвекции воздуха:
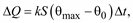 43
43
где S – поверхность проводника;
θmax и θ0 – максимальная и начальная температура провода;
k – коэффициент пропорциональности.
Приравняем количество создаваемой и количество отводимой теплоты, получим
 , 44
, 44
откуда
 45
45
Выбор структуры модели
В основе всех весьма многочисленных методов идентификации лежит идея эксперимента с «черным ящиком», которая была введена в оборот Нобертом Винером и обстоятельно развита Россом Эшби.
Идентификация является инструментом моделирования тех объектов, которые из-за сложности или недостаточной изученности, а также из-за обилия случайных факторов не могут быть исследованы на основе существующих теоретических представлений. С помощью определенных вычислительных средств и программного обеспечения (алгоритма идентификации) строится модель объекта.
На принципиальной схеме идентификации (рис. 4.3) приведены результаты наблюдений за входами x1, x2, …, xnи выходами y1, y2, …, ym объекта, и по ней с помощью алгоритма идентификации строится модель объекта.
В предельном (теоретическом) случае «черный ящик» представляет собой некоторую систему, о структуре и внутренних свойствах которой неизвестно решительно ничего. Зато входы, т. е. внешние воздействия (факторы), и выходы, представляющие собой реакции на внешние воздействия, доступны для наблюдения (измерений) в течение неограниченного времени. Задача идентификации заключается в том, чтобы по наблюдениям за входами и выходами выявить внутренние свойства объекта или, иными словами, построить его модель.
Решение задачи допускает применение двух различных стратегий.

Рис. 4.3. Принципиальная схема идентификации объекта
В первом случае осуществляется так называемый активный эксперимент, когда на вход объекта подаются специально сформированные тестовые воздействия, характер и последовательность которых определяется заранее разработанным планом. Подобный подход обладает тем преимуществом, что за счет оптимально спланированного эксперимента позволяет получить необходимую информацию о свойствах и характеристиках объекта при минимальном объеме экспериментальных данных и соответственно при минимальной трудоемкости опытных работ. Однако цена, которую приходится платить за это преимущество, достаточно высока – объект выводится из его обычного состояния, что на практике далеко не всегда возможно по принципиальным и экономическим соображениям.
Альтернативный подход заключается в том, что проводится пассивный эксперимент. Объект исследования не подвергается искусственным возмущениям и функционирует в своем естественном режиме, но при этом организуются систематические измерения и регистрации значений его входных и выходных переменных. Обработка полученных подобным путем данных в принципе позволяет получить ту же самую информацию о свойствах объекта, что и при активном эксперименте, однако необходимый объем данных существенно (на два-три порядка) больше, чем в первом случае. Естественно, что и алгоритмы обработки данных оказываются более сложными и громоздкими.
Отметим, что на практике при построении идентифицируемых моделей часто целесообразна смешанная стратегия эксперимента. По тем входным переменным объекта, которые это допускают (по условиям безопасности, техническим, экономическим соображениям и пр.), проводится активный эксперимент. Его результаты дополняются данными пассивного эксперимента, охватывающего все прочие значимые переменные. Опыт показывает, что такой подход заметно снижает трудоемкость исследований по сравнению с методикой пассивного эксперимента в чистом виде.
Ситуация «черного ящика» представляет собой теоретический граничный случай, когда о структуре объекта неизвестно абсолютно ничего. На деле исследователь всегда располагает той или иной априорной информацией об объекте идентификации, часть которой вполне достоверна (например, действие закона сохранения и других универсальных закономерностей), часть (например, сведения о структуре объекта) может носить гипотетический характер. Объем информации зависит от характера конкретной задачи и свойств объекта моделирования. Он может варьироваться в очень широких пределах, но сам факт наличия исходной информации обязателен – иначе будет невозможна осознанная постановка задачи исследования. Поэтому на практике приходится иметь дело не с «черным ящиком», а с «серым», отчасти «прозрачным» ящиком, причем можно указать три более или менее типовых уровня «прозрачности» и, следовательно, три основных класса постановки задачи идентификации объекта.
В первом, наиболее общем случае, типичном для весьма сложных и слабо изученных объектов системного характера (экологические системы, экономические процессы больших масштабов и пр.), достоверные исходные данные о внутренних свойствах и структурных особенностях объекта исчезающе малы, почти отсутствуют. Поэтому задача идентификации, казалось бы, должна включать в себя, с одной стороны, определение зависимостей, связывающих входы и выходы, с другой стороны – определение внутренней структуры объекта. Однако в такой постановке эта задача неразрешима даже теоретически.
Дело в том, что непосредственным результатом идентификации объекта является только определение зависимостей входы–выходы, причем в непараметрической форме: в виде таблиц или отображающих содержание этих таблиц кривых. Для того чтобы говорить о структуре модели, необходимо перейти к параметрической форме их представления. Однако, как известно, однозначной связи между функциональной зависимостью и порождающей эту зависимость математической структурой не существует. Каждую непараметрическую зависимость вход–выход можно аппроксимировать различными способами и соответственно построить ряд практически равноценных моделей объекта, характеризующихся собственной структурой, собственным набором параметров и их значений.
Основанием для предпочтения той или иной параметрической модели и, следовательно, фиксации модельной структуры идентифицируемого объекта могут быть только данные, внешние по отношению к процессу идентификации, полученные, например, из теоретических соображений. Если таких данных нет, то в рассматриваемой ситуации мы получаем чисто функциональную модель, которая воспроизводит с тем или иным приближением характеристики объекта, но не содержит никакой информации о его реальной структуре.
Следует отметить, что это обстоятельство, существенно ограничивающее возможности идентифицируемых моделей применительно к задачам исследования сложного объекта, далеко не всегда следует рассматривать как недостаток. Например, в задачах автоматического управления, для которых существенны именно функциональные характеристики объекта, возможность отвлечься от его реальной структуры позволяет воспроизводить необходимые характеристики объекта управления с помощью простейших одношаговых итеративных алгоритмов, которые заведомо не соответствуют протекающим в объекте реальным явлениям, но позволяют наиболее рациональным образом организовать вычислительный процесс на ЭВМ. Любопытно, что идентифицируемые модели этого класса нередко используют и в тех случаях, когда объект в принципе поддается аналитическому описанию, но последнее получается чрезмерно сложным, громоздким и неудобным для анализа. Опыт показывает, что сознательное абстрагирование от реальной структуры подобных объектов и переход к идентификации их функциональных характеристик позволяют получить вполне обозримые компактные модели, которые с достаточной точностью описывают свойства сложного объекта-оригинала.
Второй класс задач идентификации характеризуется тем, что априорные данные о структуре моделируемого объекта, полученные теоретическим путем или определенные из конструктивных соображений, в принципе имеются. Однако какой вклад в характеристики объекта или его модели вносит тот или иной структурный компонент, наперед неизвестно, и это надлежит определить на основе эксперимента наряду со значениями соответствующих параметров. Задачи этого класса, связанные с уточнениями структуры и оцениванием параметров, часто встречаются на практике и характерны для объектов и процессов средней сложности, в частности технологических, когда определенные теоретические сведения о процессе имеются, но они неполны и носят в какой-то мере гипотетический характер, так что полное аналитическое описание объекта только на основании этих данных невозможно.
Третий класс задач связан с относительно простыми и хорошо изученными объектами, структура которых известна точно, и речь идет только о том, чтобы по экспериментальным данным оценить значения всех или некоторых входящих в исследуемую структуру параметров (параметрическая идентификация). Примером такой идентификации является определение параметров четырехполюсника A, B, C, D в уравнениях
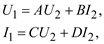
которые представляют собой модели таких объектов ЭЭС, как ЛЭП, трансформатор и пр.
Задача экспериментального оценивания или уточнения значений параметров модели возникает при исследовании подавляющего большинства реальных объектов, даже несложных и хорошо изученных.
Общую структурную схему идентификации можно представить, как показано на рис. 4.4.
Независимо от характера решаемой на основе идентификации объекта-оригинала задачи построение модели этого класса базируется на результатах измерений соответствующих величин переменных, с чем связано два существенных обстоятельства.
Во-первых, эксперимент должен быть обеспечен необходимыми средствами измерения надлежащей точности (датчиками, преобразователями, приборами). Опыт показывает, что при идентификации даже несложных, но типовых объектов, создание измерительного комплекса, прежде всего в части первичных преобразователей (датчиков) и их привязки к объекту, часто перерастает в серьезную техническую проблему. Необходимые разработки специализированных средств измерения и их компонентов, следовательно, и проведение соответствующих опытно-конструкторских работ являются в подобных случаях скорее правилом, чем исключением, а это, естественно, усложняет работы и увеличивает их стоимость.
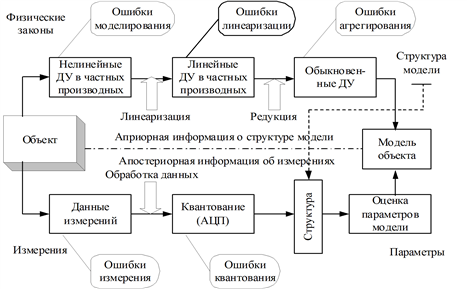
Рис. 4.4. Структурная схема идентификации объекта
Во-вторых, используемый в процессе эксперимента измерительный комплекс со всеми его компонентами требует материального обеспечения, т. е. градуировки, аттестации и периодической проверки в соответствии с нормативно узаконенным требованием. Реальная ситуация с метрическим обеспечением экспериментальной аппаратуры зависит от характера величин, подлежащих измерению в каждом конкретном случае.
Таким образом, даже при условии вполне современного технического и технологического оборудования путь от принципиальной возможности построения модели на основе идентификации до практической реализации этой возможности в большинстве случаев оказывается длинным, сложным и трудоемким. Кроме того, проведение одного эксперимента само по себе не может требовать значительных затрат, и в этом случае возникает необходимость сокращать число возможных опытов в эксперименте без ущерба для точности математической модели. Во многих случаях этому помогает оптимальное планирование эксперимента.
Вычисление параметров
Непосредственными результатами наблюдений (опытов) в процессе проведения эксперимента являются зависимости между входами x и выходами y, представленные, как правило, в табличной форме. Построение математической модели в параметрической форме требует обработки табличных данных. При этом следует учесть, что экспериментальные данные могут содержать систематические, случайные и грубые погрешности. Обычно погрешности измерений принято представлять в виде среднеквадратической погрешности σ и двумя границами интервала, в пределах которого истинное значение измеряемого параметра находится с заданной вероятностью (Δi, Δh).
На первом этапе построения математической модели необходимо выбрать вид (структуру) математической модели. Второй этап требует специальных вычислительных средств для определения параметров выбранной математической модели. Рассмотрим общий подход к подбору вида математической модели без использования каких-либо теоретических представлений о внутренней структуре моделируемого объекта. В математике такая задача носит название задачи о приближении функций. Для простоты примем объект с одним входом x и одним выходом y.
Пусть на некотором множестве задана система функций φ0(x), φ1(x), …, φm(x), которые в дальнейшем будем считать достаточно гладкими (например, непрерывно дифференцируемыми) функциями. Назовем эту систему основной.
Функции вида
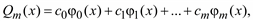
где c0, c1, …, cm – постоянные коэффициенты, называются обобщенными многочленами порядка m. В частности, если основная система состоит из целых неотрицательных степеней переменной x, т. е. φ0(x) = 1, φ1(x) = x, …, φm(x) = xm, то
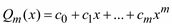
есть обычный полином степени m.
Если
то
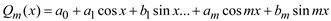
называется тригонометрическим полиномом (или тригонометрическим многочленом) порядка m.
Задача о приближении функций ставится следующим образом: данную функцию f(x) требуется заменить обобщенным многочленом Qm(x) заданного порядка m так, чтобы отклонение (в смысле σ или (Δi, Δh)) функции f(x) от обобщенного многочлена Qm(x) на указанном множестве {x} было наименьшим. При этом многочлен Qm(x) в общем случае называется аппроксимирующим.
Если множество {x} состоит из отдельных точек x0, x1, …, xn, то приближение называется дискретным. Если же {x} есть отрезок a ≤ x ≤ b, то приближение называется интегральным.
На практике часто пользуются приближениями функций обычным и тригонометрическим полиномами.
В теории дискретного приближения функций имеет место задача интерполяции функций. В случае обычного полинома задача интерполяции формулируется следующим образом. Для данной функции f(x) найти полином Qm(x) возможно низшей степени m, принимающей в заданных точках xi (i = 0, 1, 2, …, n; xi ≠ xj при i ≠ j) те же значения, что и f(x), т. е. такой, что Qm(xi) = f(xi) (i = 0, 1, 2, …, n). Такой полином называют интерполяционным, а точки xi (i = 0, 1, 2, …, n) – узлами интерполяции.
Как известно, существует единственный полином степени не выше n, принимающий в точках xi (i = 0, 1, 2, …, n) заданные значения. Поэтому можно положить n = m. Коэффициенты a0, a1, …, an полинома Qn(x) можно определить из системы уравнений:
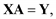 (4.11)
(4.11)
где 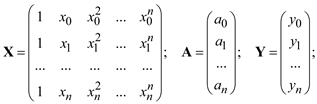
yi = f(xi) (i = 0, 1, 2, …, n).
Определитель этой системы линейных алгебраических уравнений есть так называемый определитель Вандермонда Δ ≠ 0, и, следовательно, система (4.11) имеет единственное решение.
Интерполяция дает возможность вычислить значения функции y = = f(x) между заданными точками xi – 1 и xi (i = 1, 2, …, n).
Интерполяция является частным случаем аппроксимации, когда степень интерполяционного полинома равна числу измерений без единицы и n = m (число измерений равно n + 1, а число неизвестных коэффициентов модели равно m + 1). Когда n > m, в общем случае имеем задачу аппроксимации.
Для данной функции f(x) найти полином Qm(x) степени m, который в заданных точках xi (i = 0, 1, 2, …, n; xi ≠ xjпри i ≠ j) доставляет минимум некоторой функции коэффициентов ai (i = 0, 1, 2, …, m): Sm(a0, a1, …, am). Такой полином называют аппроксимирующим. В общем случае Qm(x) есть обобщенный многочлен вида (4.7).
Функцию Sm(a0, a1, …, am) можно выбрать в соответствии с методом наименьших квадратов как сумму квадратов отклонений полинома Qm(x) от функции f(xi) на заданном множестве точек
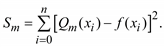 412
412
Такой способ носит название квадратичной аппроксимации.
Коэффициенты аппроксимирующего полинома Qm(x) вычисляют посредством решения системы линейных уравнений:
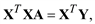 413
413
где 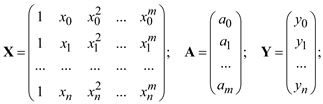
yi = f(xi) (i = 0, 1, 2, …, n) и верхний индекс T означает операцию транспонирования матрицы.
Система уравнений (4.13) получена дифференцированием критерия квадратичной аппроксимации (4.12) по искомым коэффициентам и приравниванию нулю полученных выражений. В случае обобщенного полинома (4.7) с произвольными функциями φ0(x), φ1(x), …, φm(x) в системе уравнений (4.13) вместо значений степеней x требуется подстановка значений соответствующих функций φ0(x), φ1(x), …, φm(x), вычисленных в заданных точках x.
Существуют модели, которые не являются многочленами вида (4.7) и нелинейно зависят от параметров, как, например, функция
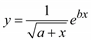 . 414
. 414
Здесь y нелинейно зависит от параметров a и b. К некоторым функциям такого вида применимо приведение нелинейной задачи к линейной по следующему способу.
Пусть задана система точек Mi(xi, yi). Вводятся новые переменные X и Y так, чтобы преобразованные точки Ni(Xi, Yi) лежали на одной прямой. Например, степенная зависимость y = cxa посредством логарифмирования приводится к линейной:
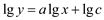 415
415
и линейная модель в новых координатах:
 416
416
Здесь Ni(Xi, Yi) = Ni(lg xi, lg yi). Некоторые функции, которые приводятся к линейной относительно коэффициентов задаче аппроксимации, представлены в табл. 4.1.
Таблица 4.1
Некоторые функции, допускающие преобразование к линейной относительно коэффициентов задаче аппроксимации
| № п/п | Исходная функция | Линейная функция | Соотношения для преобразования |
| 1 | y = axb | Y = α + bX | Y = lg y; X = lg x; α = lg a |
| 2 | y = abx | Y = α + βx | Y = ln y; α = ln a; β = ln b |
| 3 | 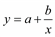
| 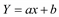
| 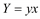
|
| 4 | 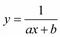
| 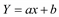
| 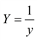
|
| 5 | 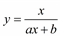
| 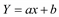
| 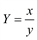
|
| 6 | 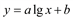
| 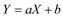
| 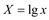
|
В тех случаях, когда невозможно перейти к линейной относительно коэффициентов задаче аппроксимации, выводятся подобные (4.13) нелинейные уравнения аналогичным способом, и их решение дает искомые коэффициенты.
Детерменированные модели
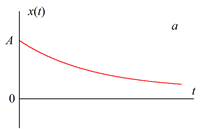
Детерминированные периодические процессы подразделяются на гармонические и полигармонические. Гармоническими называют процессы, которые могут быть описаны функцией
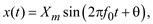 (5.2)
(5.2)
где Xm – амплитуда;
f0 – циклическая частота, измеряемая в циклах в единицу времени;
q – начальная фаза, рад.
Соотношение (5.2) может быть представлено графически в функции времени и в амплитудно-частотном изображении (спектре), как показано на рис. 5.4.
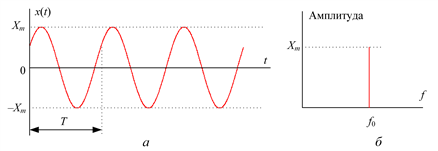
Рис. 5.4. Гармонический процесс и его спектр
Циклическая частота 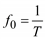 , где T – период гармонических колебаний.
, где T – период гармонических колебаний.
Полигармонические процессы описываются функцией времени, точно повторяющей свои значения через одинаковые интервалы:
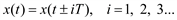 (5.3)
(5.3)
Число циклов в единицу времени называется основной частотой f1.
Полигармонический процесс может быть представлен рядом Фурье
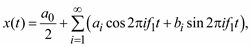 (5.4)
(5.4)
где 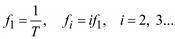 ;
;

Возможен и другой способ записи ряда Фурье для полигармонического процесса:
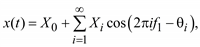 (5.5)
(5.5)
где 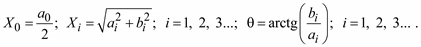
Как видно из (5.5), полигармонические процессы состоят из постоянной составляющей X0 и бесконечного числа синусоидальных составляющих, называемых гармониками, с амплитудами Xi и начальными фазами qi. Частоты всех гармоник кратны основной частоте f1.
Полигармонический процесс может имеет вид, показанный на рис. 5.5, а, и соответствующий формуле (5.5) дискретный спектр, показанный на рис. 5.5, б.
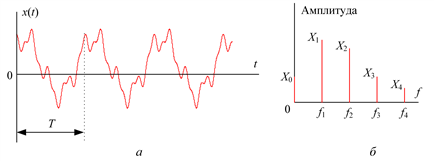
Рис. 5.5. Полигармонический процесс и его спектр
В других случаях составляющая с основной частотой может отсутствовать. Предположим, например, что периодический процесс формируется в результате сложения трех синусоидальных функций с частотами 60, 75 и 100 Гц. Наибольший общий делитель этих чисел равен 5 Гц, поэтому период результирующего периодического процесса составляет 0,2 с. Следовательно, при разложении в ряд Фурье значения Xi будут равны нулю при всех i, кроме i = 12, i = 15, i = 20.
Физические процессы полигармонического типа встречаются гораздо чаще простых гармонических процессов. В действительности, когда тот или иной процесс относят к типу гармонических, то зачастую при этом имеют в виду только приближенное представление процесса, который на самом деле является полигармоническим. Например, напряжение на выходе генератора переменного тока содержит небольшие колебания с частотами высших гармоник.
Однако процессы, образованные при суммировании двух или более гармонических функций с произвольными частотами, не будут, вообще говоря, периодическими. Сумма двух или более синусоидальных функций образует периодический процесс только в том случае, если отношение всех возможных пар частот представляет собой рациональные числа. Это означает, что существует некоторый основной период, удовлетворяющий формуле (5.3). Так, процесс
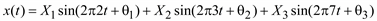 (5.6)
(5.6)
является периодическим, поскольку 2/3, 3/7 и 2/7 – рациональные числа (с основным периодом, равным единице). С другой стороны, процесс
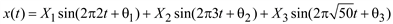 (5.7)
(5.7)
не является периодическим, поскольку числа 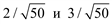 иррациональные и основной период равен бесконечности. В этом случае процесс является почти периодическим, но соотношение (5.3) не удовлетворяется при любых конечных значениях T.
иррациональные и основной период равен бесконечности. В этом случае процесс является почти периодическим, но соотношение (5.3) не удовлетворяется при любых конечных значениях T.
Таким образом, к почти периодическим относятся такие процессы, которые могут быть описаны функцией времени:
 , (5.8)
, (5.8)
имеющей хотя бы одно отношение fi / fj, которое не является рациональным числом.
Дискретный спектр почти периодического процесса аналогичен спектру полигармонического процесса.
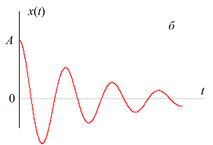
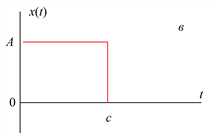
К переходным относятся все непериодические процессы, не являющиеся почти периодическими процессами, описанными выше. Другими словами, переходные процессы включают в себя все не рассмотренные ранее процессы, которые могут быть описаны подходящими функциями времени. Три примера распространенных переходных процессов приведены на рис. 5.6.
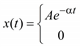
| 
|
 а
а
|
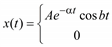
| 
|  б
б
|
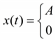
| 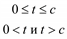
|  в
в
|
Рис. 5.6. Примеры переходных процессов
Физические переходные процессы весьма многочисленны и разнообразны. Например, процесс, изображенный на рис. 5.6, а, может описывать изменение во времени температуры проводника после отключения протекавшего по нему тока. Кривая на рис. 5.6, б может характеризовать свободные колебания инерционной механической системы после прекращения действия вынуждающей силы. График на рис. 5.6, в может описывать изменение во времени механического напряжения в тросе, который подвешен на опорах линии электропередачи и разрывается в момент c.
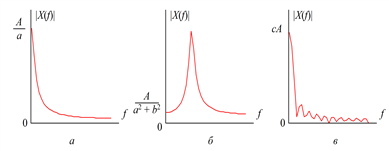
Рис. 5.7. Спектры переходных процессов
Важное отличие переходных процессов от периодических и почти периодических состоит в том, что их невозможно представить с помощью дискретного спектра. Однако в большинстве случаев получают непрерывное спектральное представление переходных процессов, используя интеграл Фурье
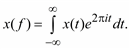
Спектр Фурье X(f) в общем случае является комплексной функцией, которая может быть записана в показательной форме:
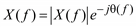 . (5.9)
. (5.9)
Здесь  - модуль, а q(f) – аргумент. Модули
- модуль, а q(f) – аргумент. Модули  преобразования Фурье трех переходных процессов, изображенных на рис. 5.6, показаны на рис. 5.7.
преобразования Фурье трех переходных процессов, изображенных на рис. 5.6, показаны на рис. 5.7.
Случайные процессы
Функция X(t) называется случайной, если ее значение при любом аргументе t является случайной величиной. Случайные функции времени называют случайными процессами.
Реализацией случайной функции X(t) (выборочной функцией) называется конкретный вид, который она принимает в результате опыта. Реализация случайного процесса может рассматриваться как элемент множества возможных физических реализаций случайного процесса (рис. 5.8). Совокупность реализаций случайного процесса называется ансамблем реализаций. Совокупность значений реализаций в фиксированный момент времени (выборка случайных значений) называется сечением случайного процесса.
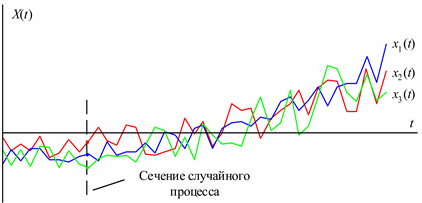
Рис. 5.8. Реализации случайного процесса
В любом сечении случайный процесс есть случайная величина.
Математическое ожидание случайного процесса есть функция времени
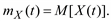 (5.10)
(5.10)
Второй центральный момент для двух сечений случайного процесса называется ковариационной функцией
 (5.11)
(5.11)
где 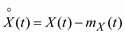 – центрированный случайный процесс.
– центрированный случайный процесс.
При t = t′ ковариационная функция равна дисперсии случайного процесса
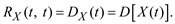 (5.12)
(5.12)
Математическое ожидание и ковариационная функция случайного процесса могут быть найдены по реализациям случайного процесса – осреднением по реализациям:
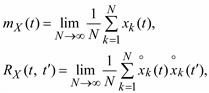 (5.13)
(5.13)
где N – число реализаций случайного процесса.
Если математическое ожидание и ковариационная функция не зависят от времени t, то процесс является стационарным:
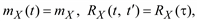 (5.14)
(5.14)
где τ = t′ – t. В (5.14) ковариационная функция зависит только от величины τ, а не от места его расположения на оси времени (рис. 5.9).
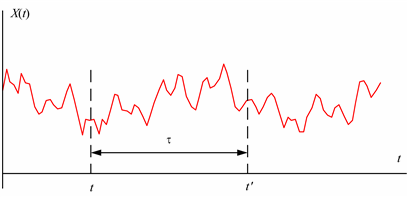
Рис. 5.9. Время между двумя сечениями случайного процесса
Возможный вид ковариационной функции показан на рис. 5.10.
Во многих случаях используется нормированная ковариационная (или корреляционная) функция. Для стационарного случайного процесса
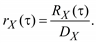 (5.15)
(5.15)
Величина корреляционной функции |rX(τ)| ≤ 1.
Возможно осреднение по времени отдельных выборочных функций (реализаций). Для k-й выборочной функции имеем:
 (5.16)
(5.16)
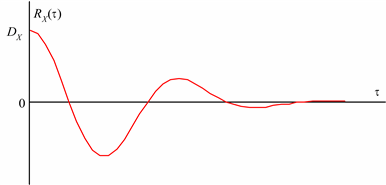
Рис.5.10. Ковариационная функция случайного процесса
Если случайный процесс X(t) стационарен и характеристики mX и RX(τ) одинаковы для различных выборочных функций, то такой процесс называют эргодическим.
Эргодические процессы представляют важный класс случайных процессов.
Нестационарными случайными процессами являются все случайные процессы, не обладающие свойствами стационарности. Эти процессы сложны в исследованиях, и зачастую в задачах по анализу их разбивают на интервалы стационарности или приближенно аппроксимируют стационарными процессами.
Прогнозирование
Прогноз - научно обоснованное суждение о возможных состояниях объекта в будущем и/или об альтернативных путях и сроках их осуществления.
Можно выделить два вида прогнозируемых характеристик системы, зависящих от времени: переменные состояния и переменные интенсивности.
Переменная состояния определяется периодически, и ее значение в течение небольшого интервала времени не зависит от времени, прошедшего с начала наблюдения. Переменная интенсивности также определяется периодически, но ее значение пропорционально времени, прошедшему с момента предыдущего наблюдения. Такие характеристики системы, как температура, скорость, число подписчиков на журнал или цена, являются примерами переменных состояния. В качестве примеров переменной интенсивности можно привести количество выпавших осадков, количество переданной электроэнергии, количество проданных экземпляров или спрос. Если переменная состояния характеризует количество, то переменная интенсивности – скорость его изменения.
Если прогноз делается в момент времени t0, то используются данные о течении процесса до этого момента. Такие данные называются ретроспективой и могут быть описаны какой-либо математической моделью физического процесса. Время, в течение которого были собраны данные о процессе, называется временем ретроспективы - Lрет. Время, на которое делается прогноз, называется временем упреждения – Lупр (рис. 5.11).
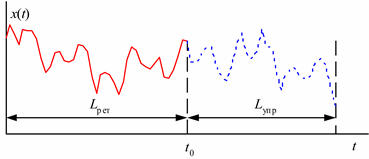
Рис. 5.11. Время ретроспективы и упреждения
Процессы прогнозирования переменных состояния и интенсивности отличаются друг от друга следующими особенностями:
· если измерения характеристик системы проводятся через равные интервалы времени, то величину интервала необходимо учитывать при оценке переменных интенсивности, в то время как при оценке переменных состояния эта величина не имеет значения;
· так как прогнозы обычно осуществляются для нескольких последовательных интервалов времени в пределах некоторого времени упреждения, по истечении которого становятся важными результаты реализации принятых решений, то правильный прогноз переменной состояния должен определять ее значение в конце времени упреждения, а прогноз переменной интенсивности должен представлять собой сумму прогнозов на протяжении времени упреждения;
· функция распределения во времени вероятностей ошибок прогноза для переменной состояния должна соответствовать функции распределения вероятностей ошибок в исходных данных, тогда как для переменной интенсивности закон распределения вероятностей ошибок прогноза во времени стремится к нормальному при любом законе распределения вероятностей ошибок в исходных данных, поскольку эти ошибки представляют собой сумму ошибок прогноза в отдельные интервалы времени.
Объектами прогнозирования могут быть процессы, явления, события.
Здесь рассматриваются вопросы прогнозирования физических процессов.
Прогноз разделяют на текущий, краткосрочный и долгосрочный. Сравнительная характеристика этих прогнозов дана в табл. 5.1.
Методы прогнозирования можно подразделить на три вида:
· статистические (описательные);
· причинно-следственные;
· комбинированные.
Статистические методы не вскрывают внутренних связей в системе и влияния внешней среды и по существу экстраполируют детерминированный или стохастический процесс по подобранной математической модели.
Причинно-следственные модели прогноза учитывают влияние окружающей среды и позволяют выделить причины изменений в системе. Прогноз, полученный по такой модели, объясняет будущее системы.
Таблица 5.1
Характеристика различных видов прогноза
| Признак |
|
| Время упреждения | 1…2 суток | До 1…2 лет | На 5…20 лет |
| Соотношение Lупри Lрет | |||
| Тип используемой информации | Непрерывные процессы | Интервальная | Интервальная качественная |
| Основные гипотезы | Стационарность, эргодичность, устойчивость средних | Устойчивость тенденций | Неустойчивость и неравномерность развития |
| Определяющие законы функционирования | Физические, вероятностные | Системные, причинно-следственные | Эволюционные |
Если процесс является периодическим, то частота наблюдений должна быть, по крайней мере, вдвое больше частоты изучаемого процесса.
Важное значение имеет анализ исходных данных для прогнозирования. Данные являются результатами выборочных наблюдений, в которых возможны выбросы, т. е. значения, которые появились в результате аномальных эффектов (чрезвычайно большая температура в помещении вследствие поломки кондиционера, большой спрос на продукцию во время забастовок, изменение потребления электроэнергии
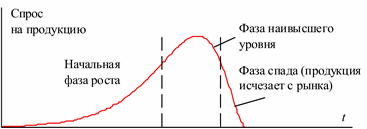
Рис. 5.12. Кривые жизненного цикла продукции
в период экономических и социальных перемен и т. п.). Поэтому не всякая совокупность является подходящим временным рядом, и перед построением модели прогноза необходимо из данных исключить выбросы, которые не характеризуют прогнозируемый процесс.
Некоторые процессы поддаются графоаналитическому описанию в силу некоторых физических, экологических и даже экономических закономерностей, Так, например, замечена закономерность появления и спада спроса на некоторую продукцию на рынке (рис. 5.12). Известны и хорошо подтверждаются на практике экологические модели размножения и гибели популяций.
Дата: 2019-07-30, просмотров: 622.