Одной из типовых задач статистической обработки случайных векторов является выяснения наличия зависимостей между отдельными их компонентами. Например, в Примере 15 в анкете может быть вопрос о доходе респондента 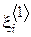 и вопрос о его возрасте  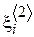и исследователь планирует при помощи эксперимента проанализировать, есть ли взаимосвязь между этим величинами.

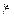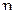Одним из простейших видов зависимости между случайными величинами является линейная корреляция. По определению, коэффициентом линейной корреляции (или просто коэффициентом корреляции) между двумя случайными величинами  и  вычисляется исходя из следующего выражения:

              ,         

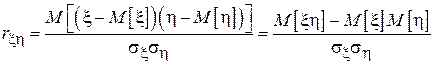где 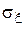 и 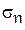 - среднеквадратические отклонения первой и второй случайной величины соответственно. Коэффициент  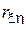может принимать значения в диапазоне [-1, +1]. Значение 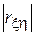, близкое к единице, говорит о высокой коррелированности (а, значит, и зависимости) между  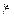и 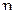, причем положительный знак указывает на положительную корреляцию (условно говоря, в среднем, чем  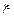больше, тем  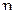- больше), отрицательный знак – на отрицательную корреляцию (наоборот, чем  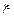больше, тем, в среднем,  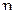- меньше).

Пример 18.

В ходе эксперимента, у случайно выбранного участника регистрируют рост 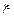 и вес 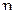. Очевидно, что .

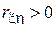Пример 19.

В ходе испытания мобильной сети, в случайных точках города производится замер расстояния до ближайшей базовой станции 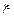 и максимальной скорости приема данных 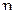. В силу того, что с ростом расстояния сигнал ослабевает и скорость падает, .

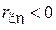Замечание.

Так как коррелированность – это всего лишь один из возможных типов зависимости, из некоррелированности ( 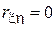), вообще говоря, не следует независимости случайных величин.

Одним из стандартных способов оценивания 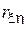 по выборке  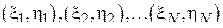является выборочный коэффициент корреляции, определяемый следующим выражением:

                                       .                                   

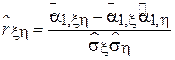Здесь:

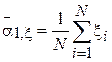-  - выборочное математическое ожидание случайной величины ;

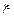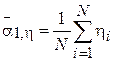-  - выборочное математическое ожидание случайной величины ;

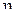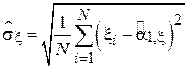-  - выборочное СКО случайной величины ;

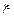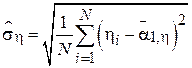- - выборочное СКО случайной величины ;

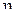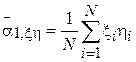-  - выборочный первый смешанный момент случайных величин  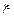и .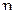

Дадим выборочному коэффициенту корреляции следующую наглядную интерпретацию. Построим график, на который нанесем точки, соответствующие всем парам 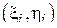 (так называемая диаграмма рассеяния или облако) и проведем через облако прямую линию вида 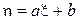. Коэффициенты этой прямой a и b подберем так, чтобы эта прямая проходила через облако с минимальной невязкой относительной точек :

                           .

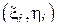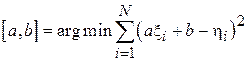Такая прямая называется линейной регрессией для выборочных данных 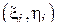. Тогда выборочный коэффициент корреляции будет прямо пропорционален полученному коэффициенту наклона этой прямой a:

.

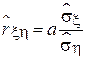Примеры диаграмм рассеяния с проведенными прямыми см. на рис. 5.1а – 5.1г.

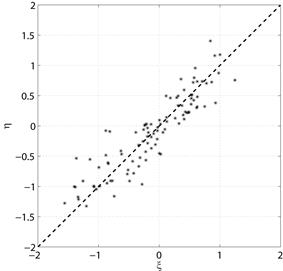а) Положительная корреляция	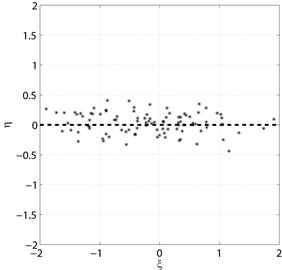б) Нулевая корреляция
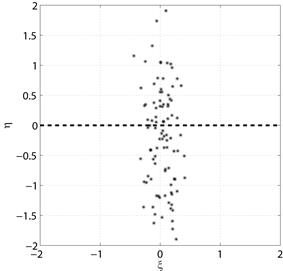в) Нулевая корреляция	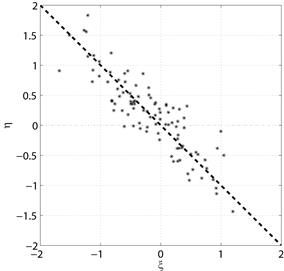г) Отрицательная корреляция

Рис. 5.1. Диаграммы рассеяния