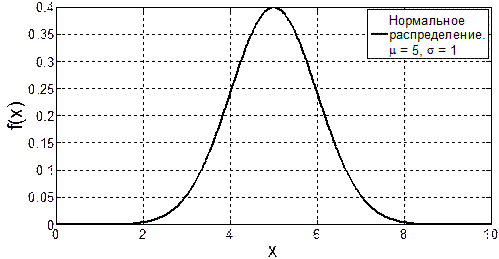
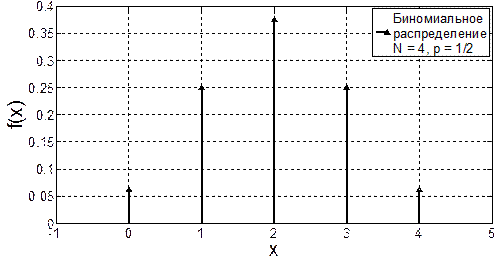
Среди наиболее распространенных способов оценивания смещения симметричного распределения можно выделить следующие четыре: выборочное среднее, усеченное среднее, выборочная медиана, середина размаха. Рассмотрим подробнее особенности применения, достоинства и недостатки каждой из них.

Рис. 3.1. Примеры симметричных распределений

Выборочное среднее.

Выборочное среднее является простейшей оценкой смещения случайной величины:

                                                   .                                  

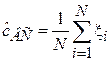Данный тип оценки был подробно рассмотрен в предыдущем разделе. Здесь отметим, что в случае, если дисперсия случайной величины равна бесконечности, скорость сходимости оценки к истинному значению может быть существенно медленнее, чем 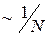, определяемое в Свойствах 2-3 Раздела 2.1. В случае же, если не существует математическое ожидание, выборочное среднее является несостоятельной оценкой смещения симметричного распределения и не применимо в принципе.

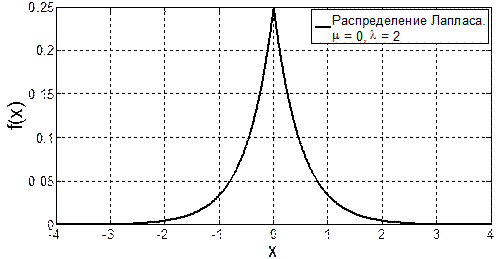
В частности, это справедливо для так называемых "тяжелохвостных" распределений, пример одного из которых (распределения Коши) приведен на рис. 3.2. На графике видно, что, не смотря на кажущуюся схожесть, плотность вероятности Коши имеет одно важное отличие от нормальной плотности, а именно существенно более медленную скорость спадания "хвостов" (обведено на рисунке).

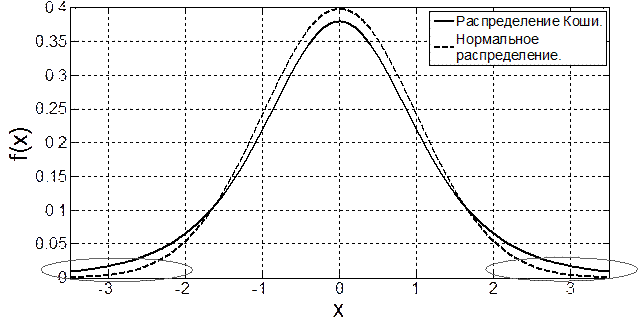
Рис. 3.2. Сравнение распределения Коши и нормального распределения

Таким образом, случайная величина, распределенная по закону Коши, с высокой вероятностью принимает значения, существенно отклоняющиеся от точки смещения. Эти большие значения (выбросы) сильно искажают результирующую сумму (3.3) и делают оценку несостоятельной. Данный негативный эффект может быть частично устранен при помощи метода усечения выборки.

Усеченное среднее.

Основной идеей данного метода является предварительное удаление из выборки т.н. выбросов, сильно отклоняющихся от центра распределения величин. Для этого элементы выборки вначале упорядочиваются в порядке возрастания. Получившаяся в результате последовательность 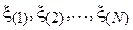 называется вектором порядковых статистик, а ее i-й элемент  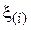– i -й порядковой статистикой. После этого из выборки удаляются kN первых и kN последних элементов, а от оставшихся считается среднеарифметическое:

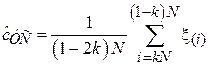
Доля удаляемых элементов k называется коэффициентом усечения и обычно выбирается в диапазоне 0.05-0.2. Чем больше величина k, тем устойчивее оценка к наличию выбросов в выборке, но тем меньше ее эффективность в случае, когда выборка выбросов не содержит. Классическим примером использования усеченного среднего является подсчет среднего балла на спортивных соревнованиях: из выставленных судьями оценок отбрасывается самая маленькая и самая большая оценки. Таким образом, организаторы соревнований борются с намеренным занижением или завышением балла в случае ангажированности судей.

Предельным случаем усеченного среднего, когда из вектора порядковых статистик удалены все элементы кроме центрального, называется метод выборочной медианы.

Выборочная медиана.

Выборочная медиана получается путем отбрасывания из вектора порядковых статистик всех элементов, кроме центрального (в случае, если N – нечетное), либо двух центральных (если N – четное):

                    .    

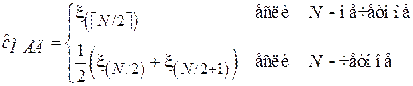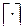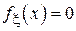Здесь символ  обозначает округление вверх до ближайшего целого. Выборочная медиана является одной из наиболее устойчивых к выбросам оценок, однако неприменима в случае, когда медиана исходного распределения  не может быть однозначно определена (т.е. когда  в окрестности точки смещения c).

Середина размаха.

В случае, когда известно, что распределение элементов выборки 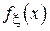 задано на ограниченном интервале, хорошие результаты может давать следующая оценка смещения c:

                                                ,                               

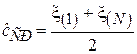т. е. среднеарифметическое значение минимального и максимального элементов выборки. Однако, если 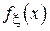 отлична от нуля на бесконечном интервале, в большинстве случаев оценка окажется несостоятельной.

Далее, в таблице 3.1 приведена сводная информация по 4-м рассмотренным оценкам параметра смещения случайной величины с симметричным распределением.

Таблица 3.1 – Сводная информация по методам оценки смещения

Название метода	Формула оценки	Область применения	Дисперсия оценки
Выборочное среднее		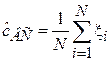Оценка является состоятельной при существовании первого начального момента. Указанная дисперсия гарантируется при существовании второго центрального момента.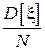
Усеченное среднее[5]		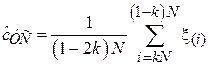Применима для широкого класса распределений.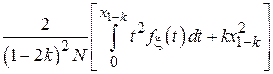
Выборочная медиана		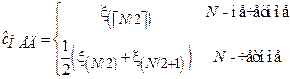Оценка является состоятельной с указанной дисперсией при однозначности определения медианы распределения и конечности .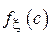
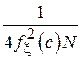
Середина размаха		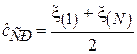Оценка является состоятельной при ограниченности области определения случайной величины.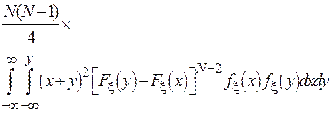

Вопросы для самопроверки

1. В каком случае медиана распределения не может быть однозначно определена? Приведите пример.

2. Почему график зависимости дисперсии оценки от объема выборки, построенный в логарифмическом масштабе, представляет собой прямую линию?

3. Для заданного распределения проверьте зависимость среднего квадрата ошибки оценки смещения по выборочному среднему от объема выборки с помощью теоретического выражения (см. таблицу 3.1).

4. Для заданного распределения проверьте зависимость среднего квадрата ошибки оценки смещения по выборочной медиане от объема выборки с помощью теоретического выражения (см. таблицу 3.1).

5. Для заданного распределения проверьте зависимость среднего квадрата ошибки оценки смещения по усеченному среднему от объема выборки с помощью теоретического выражения (см. таблицу 3.1).

6. Вывести формулу дисперсии оценки смещения биномиального распределения 2-го порядка по середине размаха.

7. Предложите свою оценку смещения и проведите ее исследование методом моделирования.

8. Доказать, что у распределения Коши не существует математического ожидания.

9. Доказать, что у распределения Коши второй начальный момент равен бесконечности.

10. Для заданного распределения теоретически сравнить эффективность двух оценок – выборочного среднего и выборочной медианы.

11. Вывести выражение для 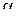-квантиля экспоненциального распределения.

12. Вывести выражение для 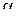-квантиля равномерного распределения.

13. Доказать, что разница независимых одинаково распределенных случайных величин имеет симметричное распределение.

14. Дано:

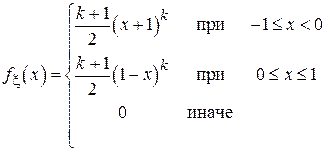
Сравните теоретически эффективности оценок смещения для данного распределения по выборочной медиане и по середине размаха для k = 1.

15. Как зависит эффективность оценки смещения для данного распределения по выборочной медиане от параметра k (см. вопрос 14)?

16. Как зависит эффективность оценки смещения для данного распределения по середине размаха от параметра k (см. вопрос 14)?

17. Выведите выражение для плотности вероятности разности двух независимых случайных величин, распределенных по равномерному закону с параметрами a и b.

18. Выведите выражение для ряда распределения двух независимых случайных величин, распределенных по биномиальному закону с параметрами N и p.

19. Выведите выражение для плотности вероятности разности двух независимых случайных величин, распределенных по экспоненциальному закону с параметром .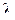

20. Выведите выражение для плотности вероятности разности двух независимых случайных величин, распределенных по гауссовскому закону с параметрам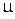и  и .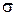

4. Оценка закона распределения случайной величины