Основная схема проведения статистического эксперимента приведена на рис. 1.1. Есть некоторый объект, обладающий параметром (свойством) или набором параметров 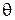, интересующих исследователя. Ограниченность доступа к объекту или сложность его организации могут служить препятствием к непосредственному выяснению 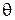. Тогда можно прибегнуть к проведению испытаний с объектом или просто наблюдением за конкретными проявлениями его функционирования, набрав таким образом экспериментальные данные (как правило, количественные). Данная последовательность чисел  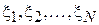называется выборкой, каждый отдельный результат наблюдения (испытания) 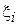– элементом выборки, N – объемом выборки. Так как исследователю результаты наблюдений заранее неизвестны, то для него элементы выборки являются случайными числами. Далее, при помощи некоторого формального правила (алгоритма) по выборке производится оценка параметра .

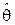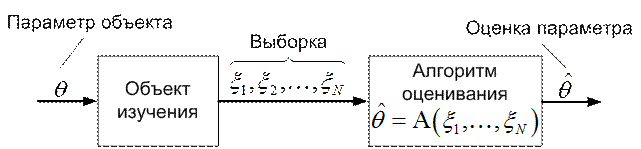
Рис. 1.1. Общая схема статистического эксперимента

Пример 1.

Пусть объектом изучения является лекарственный препарат, а задачей исследования – выяснение его эффективности : например, насколько в среднем уменьшается уровень холестерина в крови в случае его приема. Очевидно, что в силу сложности биохимических реакций в организме человека теоретический расчет данной величины едва ли возможен. Тогда прибегают к постановке следующего эксперимента: группе добровольцев замеряют уровень холестерина до приема препарата и после. В данном примере: N соответствует числу пациентов, участвующих в эксперименте,  - тому, на сколько ммоль/л уменьшился уровень холестерина у i-го пациента после приема препарата. Можно предложить следующий несложный алгоритм оценивания: .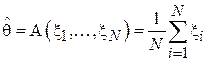

Пример 2.

Как правило, заказчик информационной системы в техническом задании выдвигает к разработчику требования по быстродействию. Например, требование может быть следующим: время отклика системы на запрос пользователя с высокой вероятностью (например, 0.99) не должно превышать заданного порога h. Тогда 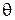 – вероятность того, что время выполнения превысит h. Для того, чтобы доказать соответствие разработки данному требованию формируется N запросов, для каждого из которых регистрируется время выполнения . Тогда простейшим алгоритмом будет 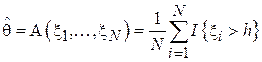. Здесь  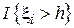- индикаторная функция, принимающая значение 1, если 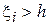, и 0 иначе.

При дальнейшем изложении, если не оговорено отдельно, будем полагать, что все эксперименты проводятся при одинаковых условиях и независимо друг от друга. Тогда можно считать, что 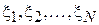 является выборкой независимых, одинаково распределенных случайных величин[2].

Зачастую, для оценивания 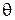 можно предложить сразу несколько алгоритмов (оценок), что приводит к необходимости введения формальных критериев качества их работы. Кратко напомним о способах представления случайных величин, а затем рассмотрим три основных свойства оценок, позволяющие сравнивать их между собой с тем, чтобы выбрать наилучшую.