В курсе теории вероятности рассказывалось, что случайная величина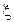 
полностью характеризуется своей интегральной функцией распределения 
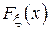[2]. По определению:
,
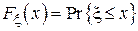т.е. вероятность того, что данная случайная величина примет значение, не превосходящее x.
Для дискретно-распределенной случайной величины вторым способом описания является ряд распределения, т.е. упорядоченное множество возможных значений случайной величины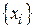 
и множество соответствующих им вероятностей 
, 
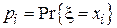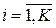(K – количество возможных значений случайной величины).
Для непрерывной случайной величины условным аналогом ряда распределения является плотность вероятности (дифференциальная функция распределения)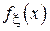 
:
,
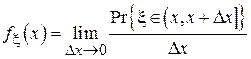т.е. отношение вероятности попадания случайной величины в малый интервал к длине этого интервала. Учитывая свойства интегральной функции распределения, можно выписать пару преобразований (1.3)-(1.4), однозначно связывающих интегральную и дифференциальную функции распределения:
,
.
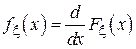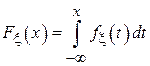Иногда исследователя может интересовать не сама наблюдаемая в эксперименте случайная величина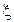 
, а некоторая функция 
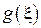от нее.
Пример 3.
В физической лаборатории анализируются возможные значения кинетической энергии частиц. Однако лабораторная установка позволяет измерять только их скорости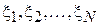 
. Тогда 
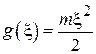и далее работа идет уже с выборкой 
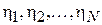, где 
.
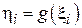Введем следующее стандартное обозначение:
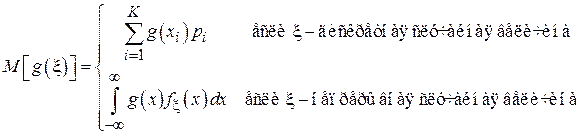
Вычисленная по данной формуле величина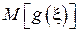 
соответствует среднему значению функции 
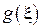(например, для Примера 1 - средней энергии частицы).
Частичную информацию о случайной величине содержат так называемые моменты. Для большого класса задач является достаточным знание лишь отдельных моментов случайной величины, поэтому важной задачей является их оценка по выборке.
По определению, начальным моментом k -го порядка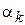 
называется следующая величина:
.
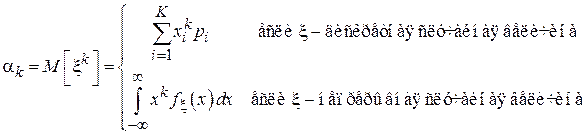Таким образом, неформальным определением начального момента является среднее значение случайной величины, возведенной в степень k. Отдельно стоит отметить случай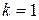 
(первый начальный момент). Момент 
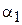называется математическим ожиданием (МО) случайной величины 
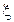, характеризует ее среднее значение и традиционно обозначается через 
.
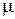Центральный момент k -го порядка определяется в выражении (1.6).
.
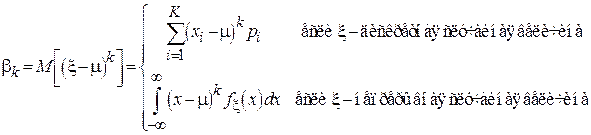Центральный момент 2-го порядка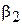 
называется дисперсией случайной величины и характеризует меру разброса случайной величины относительно среднего значения. Дисперсия также обозначается через 
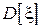. На практике зачастую удобней работать не с самой дисперсией, а с ее корнем – среднеквадратическим отклонением 
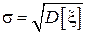(СКО). Интерпретация других центральных моментов, третьего и четвертого, будет дана в разделе 4.
Раскрыв скобки в подынтегральном выражении (1.6) и учитывая (1.5) можно получить следующее выражение для центрального момента:
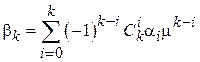
Так, в частности, дисперсия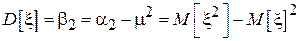 
.
Замечание. В случае если при вычислении интегралов (1.5)-(1.6) для некоторых k появляется неопределенность, соответствующие моменты случайной величины не существуют. Далее, если не будет оговорено отдельно, везде будем полагать, что рассматриваемые интегралы существуют и являются сходящимися.
Свойства оценок
Несмещенность
Так как оценка является функцией от нескольких случайных величин (элементов выборки), то очевидно, что и сама оценка является случайной величиной. Таким образом, оценка может принимать значение как превышающее истинное, так и, наоборот, заниженное. Естественным желанием является то, чтобы в среднем оценка совпадала с истинным значением, т.е.:
.
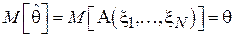Такая оценка называется несмещенной. Можно ввести величину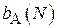 
, характеризующую величину смещения, вносимого при использовании алгоритма 
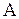по выборке объема N:
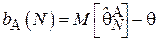
Здесь и далее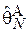 
обозначает оценку параметра 
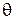при помощи алгоритма 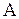по выборке объема N. Если 
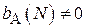, то оценка является смещенной. Возможны также случаи, когда для конечного N оценка – смещенная, но:
.
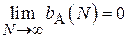Данная оценка называется асимптотически несмещенной. Т.е. при достаточно большом объеме выборки N, величиной смещения можно пренебречь.
Пример 4.
При анализе трафика, передаваемого с сервера на компьютеры клиентов, производится оценка среднего размера пакета передаваемого по сети. Для этого из общего потока выбирается N пакетов, размеры которых фиксируются и усредняются. В данном примере случайная величина 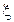характеризует размер пакета, искомый параметр 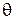- среднее значени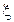е (т.е.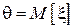 
), элементы выборки 
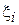- размеры зарегистрированных пакетов, алгоритм оценивания 
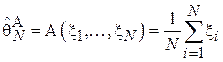. Проверим, является ли данная оценка смещенной:
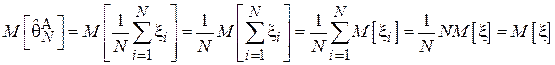
Таким образом, данная оценка является несмещенной.
Пример 5.
Пусть известно, что время отклика базы данных на запрос пользователя является равномерно распределенной случайной величиной в диапазоне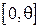 
. Задачей исследователя является выяснение величины 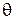- т.е. худшего случая, при котором задержка максимальна. Применяется следующая оценка: 
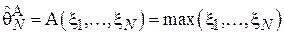, т.е. максимальная задержка, зарегистрированная в ход проведения эксперимента, состоящего из N запросов. Для упрощения выкладок при проверке смещенности данной оценки введем следующее обозначение для максимального элемента выборки 
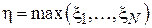(т.е. 
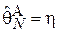и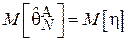 
). Найдем интегральную функцию распределения величины 
:
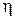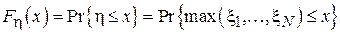
Для того чтобы максимальный элемент выборки не превосходил x, необходимо и достаточно, чтобы каждый элемент выборки не превосходил x. Обратное также верно. Тогда, учитывая независимость случайных величин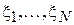 
получим:
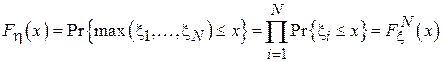
Учитывая, что функция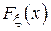 
описывает равномерное распределение в диапазоне 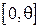, получим:
.
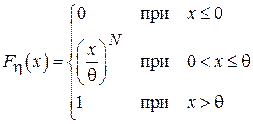Воспользовавшись формулой (1.3) получим выражение для плотности вероятности :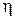
.
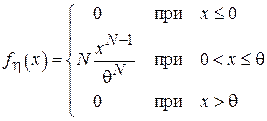Тогда:
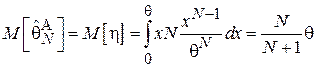
Таким образом, данная оценка является смещенной, причем:
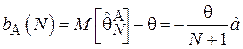
Очевидно, что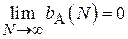 
и рассмотренная оценка является асимптотически несмещенной.
В тех случаях, когда величина смещения может быть вычислена заранее, смещенная оценка может быть превращена в несмещенную:
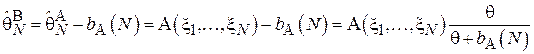
Так, например, для оценки, рассмотренной в Примере 5, несмещенный вариант имеет следующий вид:
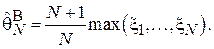
Состоятельность
При обработке выборки исследователь интуитивно предполагает, что, чем больше ее объем, тем ближе будет оценка к истинному значению. Т.е. с ростом N, ошибка в оценивании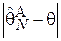 
должна стремиться к нулю. Это возможно, если алгоритм оценки эффективно использует ту информацию об искомом параметре, которая содержится в выборке.
Формально данное свойство определяется следующим образом: оценка является состоятельной, если 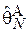сходится по вероятности к :
.
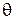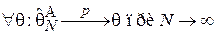Сходимость по вероятности в свою очередь означает, что для любого, сколь угодно малого, отличного от нуля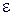 
:
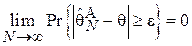
То есть всегда найдется такой объем выборки, который с вероятностью, близкой к единице обеспечит необходимую величину ошибки в оценивании 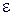, какой бы малой она не была.
Пример 6.
Рассмотрим оценку из Примера 4 и выясним, является ли она состоятельной. Эта оценка является несмещенной, а, значит,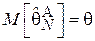 
и можно применить второе неравенство Чебышёва:
.
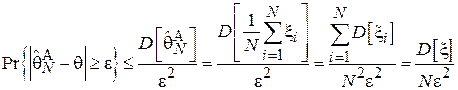Очевидно, что при конечной 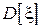для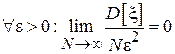 
, что доказывает состоятельность рассмотренной оценки.
При помощи аналогичных рассуждений можно показать, что оценка из Примера 5 также является состоятельной.
Эффективность
Предположим, что для проведения эксперимента перед исследователем стоит выбор одного из двух алгоритмов оценивания искомого параметра системы. Оба алгоритма обеспечивают оценки несмещенные и состоятельные. Как осуществить выбор одного из них? Для ответа на этот вопрос вводят третий параметр оценки – параметр эффективности. Прежде, чем дать формальное определение эффективности, дадим ее качественную интерпретацию. На рис. 1.2 для двух гипотетических оценок приводятся графики зависимости погрешности оценивания от объема выборки. Не смотря на то, что оба алгоритма обеспечивают сколь угодно малую погрешность при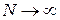 
, при конечном N алгоритм 2 явно кажется более предпочтительным, т.е. оценка 2 эффективнее оценки 1.
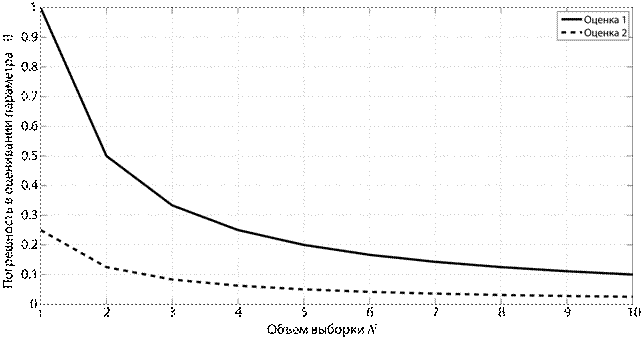
Рис. 1.2. Сравнение двух алгоритмов оценивания
Чтобы количественно измерять эффективность введем несколько вспомогательных функций.
Функцией штрафа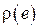 
называется функция, характеризующая меру негативных последствий, возникающих при той или иной ошибке e оценивания параметра системы. Как правило, чем больше 
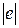, тем больше значение 
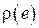. Функция штрафа выбирается исходя из специфики той предметной области, в которой ведется статистический анализ и может принимать достаточно сложный вид.
Пример 7.
По данным Гидрометцентра проводится оценка количества осадков, выпавших в некотором регионе. Из количества осадков рассчитывается тип и объем удобрений, которые необходимо применить на сельскохозяйственном поле. Известно, что неправильно выбранный режим удабривания приводит к падению количества урожая. Тогда, функция штрафа может иметь, например, вид, приведенный на рис. 1.3.
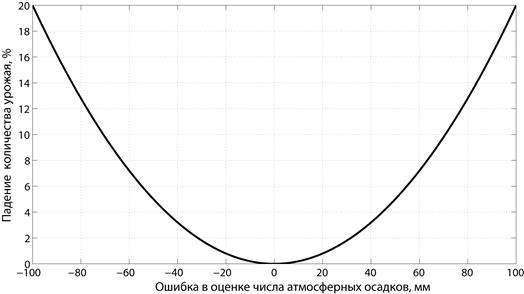
Рис. 1.3. Функция штрафа в Примере 7
Пример 8.
В ходе работы телекоммуникационной системы приемник периодически проводит оценку мощности шумов, присутствующих в канале. Этот уровень учитывается в процессе декодирования принимаемого сообщения. Известно, что ошибочно введенная в декодер информация о шумах повышает вероятность битовой ошибки при приеме данных. При этом заниженная оценка мощности приводит к существенно большему ухудшению качества приема, нежели завышенная. Типичная функция штрафа приведена на рис. 1.4.
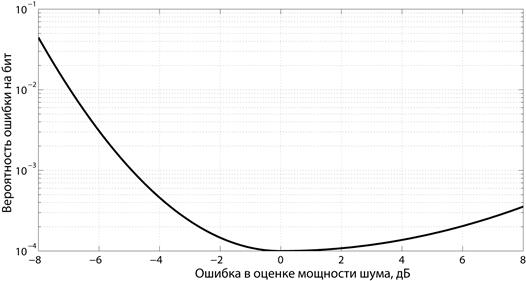
Рис. 1.4. Функция штрафа в Примере 8
Как правило, многие реальные функции штрафа могут быть хорошо аппроксимированы так называемой квадратичной штрафной функцией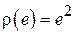 
или абсолютной штрафной функцией 
.
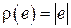Оценка параметра является случайной величиной, а, значит, ошибка в оценивании и величина штрафа также являются случайными величинами. Таким образом, вводят функцию риска:
.
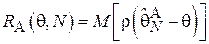Т.е. функция риска характеризует средний штраф, который заплатит исследователь при использовании алгоритма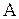 
для оценки параметра 
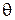по выборке объема N. Более эффективной является та оценка, которая обеспечивает меньший риск.
Заметим, что для несмещенных оценок в случае применения квадратичной штрафной функции:
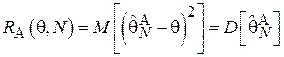
Т.е. функция риска совпадает с дисперсией оценки (см. выражение (1.6)).
Как можно видеть, функция риска зависит как от объема выборки, так и от истинного значения параметра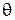 
. Таким образом, для различных диапазонов значения 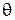разные оценки могут оказаться более или менее эффективными. При этом ожидается, что для состоятельных оценок 
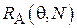убывает с ростом N. Проиллюстрируем эти зависимости в Примерах 9 и 10.
Пример 9.
Проводится эксперимент, в ходе которого выясняется вероятность потери пакета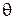 
при передаче по вычислительной сети. Для этого по сети передаются N тестовых пакетов, успешный прием или потеря которых регистрируется на приемной стороне. Вводится величина 
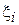, равная единице, в случае, если i-й пакет оказался утерянным, и нулю иначе. Тогда воспользуемся следующей несложной оценкой: 
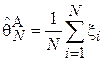. Найдем выражение 
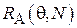для случая применения квадратичной штрафной функции. Очевидно, что 
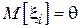, тогда:
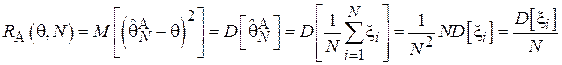
Т.к.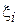 
является Бернуллиевской случайной величиной с параметром 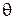, то:
.
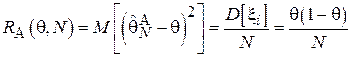Пример 10.
Для той же задачи из Примера 9 можно также предложить другую, менее очевидную оценку для 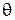(оценку Лемана-Ходжеса):
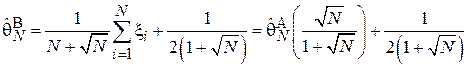
Тогда:
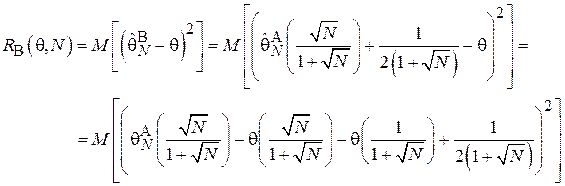
Перегруппировав слагаемые и вынеся константы за знак математического ожидания получим:
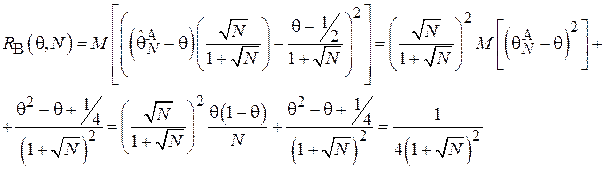
На рис. 1.5 и 1.6 для обеих оценок приведены графики зависимости функций риска от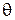 
(при N = 10) и от N (при 
).
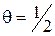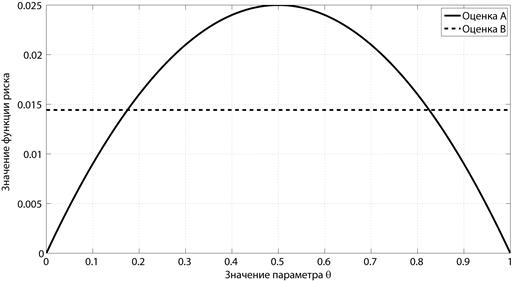
Рис. 1.5 Зависимость риска от значения параметра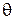 
при объеме выборки N = 10 (Примеры 9 и 10)
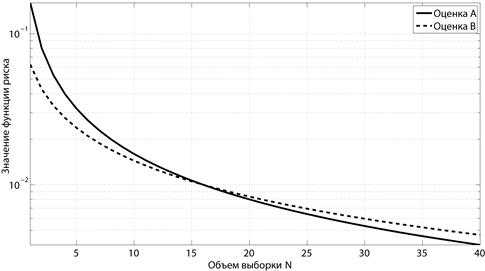
Рис. 1.6 Зависимость риска от объема выборки при значении параметра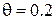 
(Примеры 9 и 10)
Более подробно особенности поведения функции риска будут проанализированы в Разделе 3 на примере оценки смещения симметричного распределения.
Вопросы для самопроверки
1. Выведите формулу для математического ожидания гауссовской случайной величины.
2. Выведите формулу для дисперсии гауссовской случайной величины.
3. Выведите формулу для расчета центрального момента через начальные моменты (см. стр. 10).
4. Как определить вероятность попадания случайной величины в заданный интервал с помощью плотности вероятности и интегральной функции распределения? Привести пример.
5. Какими преобразованиями связаны между собой интегральная и дифференциальная функции распределения? Приведите пример пересчета.
6. Доказать первое неравенство Чебышева. Привести пример его использования.
7. Доказать второе неравенство Чебышева. Привести пример его использования.
8. Является ли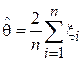 
несмещенной оценкой для правой границы диапазона значений равномерно распределенной случайной величины [0, 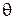]? Если оценка окажется смещенной, найти величину смещения (см. Пример 5).
9. Является ли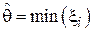 
несмещенной оценкой для левой границы диапазона значений равномерно распределенной случайной величины [ 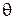,5]? Если оценка окажется смещенной, найти величину смещения (см. Пример 5).
10. Является ли оценки вероятности бернуллиевской случайной величины из Примера 9 смещенной?
11. Является ли оценка Лемана-Ходжеса из Примера 10 смещенной?
12. Поясните смысл понятий «сходимость по вероятности» и «состоятельность».
13. Является ли оценки вероятности бернуллиевской случайной величины из Примера 9 состоятельной.
14. Является ли оценка Лемана-Ходжеса из Примера 10 состоятельной?
15. Проверьте методом моделирования формулу для функции риска оценки вероятности бернуллиевской случайной величины из Примера 9.
16. Проверьте методом моделирования формулу для функции риска оценки Лемана-Ходжеса (см. Пример 10).
17. Предложите оценку параметра N биномиальной случайной величины. Проанализируйте ее смещенность.
18. Предложите оценку параметра N биномиальной случайной величины. Проанализируйте ее состоятельность.
19. Постройте методом моделирования функцию риска для оценки вероятности бернуллиевской случайной величины из Примера 9 при использовании абсолютного штрафа.
20. Постройте методом моделирования функцию риска для оценки вероятности бернуллиевской случайной величины из Примера 10 при использовании абсолютного штрафа.
2. Общие методы оценки параметров случайной величины
Дата: 2019-07-24, просмотров: 199.
