До этого момента рассматривались различные алгоритмы и критерии качества оценивания отдельных параметров распределения. Однако на практике часто возникает задача оценивания самого закона распределения.
Т.к. распределение случайной величины в равной степени характеризуется функцией плотности вероятности и интегральной функцией распределения, можно выделить два классических подхода к оцениванию:
1. оценка плотности вероятности методом гистограмм;
2. оценка через эмпирическую интегральную функцию распределения.
Также в последнее время широкое распространение получили методы экспресс-оценки закона распределения через оценку отдельных моментов случайной величины. В данном разделе будет дана базовая информация по всем трем подходам.
Метод гистограмм
В основе метода гистограмм лежит идея об аппроксимации плотности вероятности 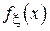 при помощи ступенчатой функции по следующему принципу.
при помощи ступенчатой функции по следующему принципу.
Известно, что вероятность попадания случайной величины в заданный интервал [a, b] находится из следующего выражения:
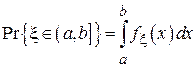
При малой длине (a, b] функцию 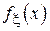 можно считать на этом интервале почти постоянной и можно воспользоваться следующим приближением:
можно считать на этом интервале почти постоянной и можно воспользоваться следующим приближением:
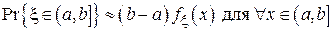 .
.
Тогда:
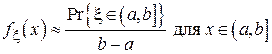 .
.
Соответственно можно разбить область определения случайной величины 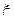 на M непересекающихся интервалов
на M непересекающихся интервалов 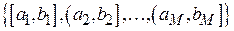 и на каждом интервале аппроксимировать плотность вероятности при помощи выражения (4.1). Очевидно, что чем больше M и меньше длительности интервалов
и на каждом интервале аппроксимировать плотность вероятности при помощи выражения (4.1). Очевидно, что чем больше M и меньше длительности интервалов 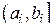 , тем более точной будет аппроксимация (см., например, рис. 4.1, на котором приведены аппроксимации плотности распределения закона Симпсона при M = 11 и M = 31).
, тем более точной будет аппроксимация (см., например, рис. 4.1, на котором приведены аппроксимации плотности распределения закона Симпсона при M = 11 и M = 31).
а) 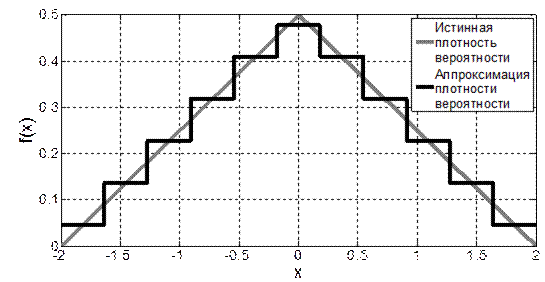
б)
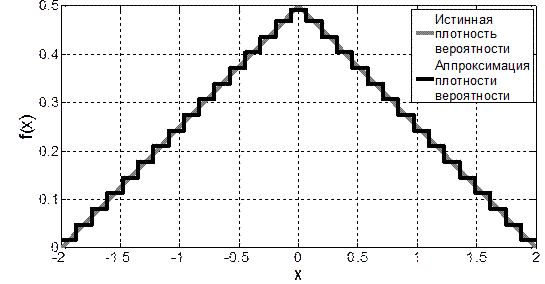
Рис. 4.1. Графики аппроксимации ПВ закона Симпсона при М=11 и M =31
По выборке можно осуществить оценку 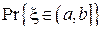 следующим образом:
следующим образом:
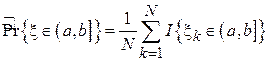 ,
,
где N – объем выборки, 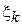 - k-й элемент выборки,
- k-й элемент выборки, 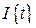 - индикатор события t. Тогда оценка плотности вероятности будет иметь следующий вид:
- индикатор события t. Тогда оценка плотности вероятности будет иметь следующий вид:
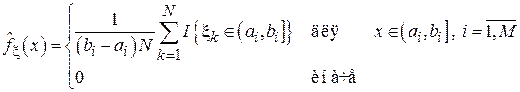
Графическое изображение функции (4.3) называется гистограммой и имеет характерный ступенчатый вид (см., например, рис. 4.2). Очевидно, что гистограмма будет задана на интервале [a1, bM].
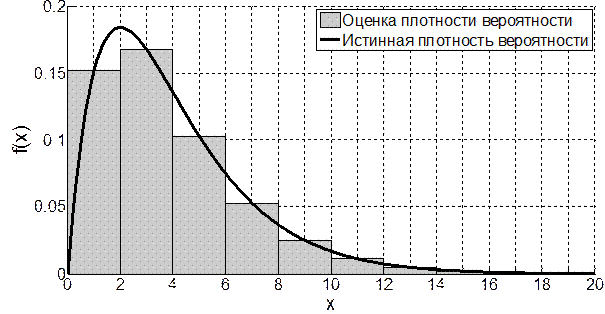
Рис. 4.2. График плотности распределения хи-квадрат и построенной гистограммы
Для применения выражения (4.3) приходится решать ряд практических вопросов, таких, например, как оценка области определения случайной величины, выбор числа интервалов M, границы интервалов (ai, bi] и т. д. Ниже приведем некоторые стандартные рекомендации.
1. Число интервалов разбиения выбирать исходя из правила Стерджеса: 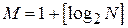 , где N – объем выборки,
, где N – объем выборки, 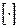 – знак округления.
– знак округления.
2. В некоторых источниках можно встретить следующую рекомендацию к выбору границ области построения гистограммы: 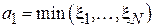 ,
, 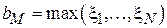 . Стоит, однако, иметь в виду, что такой подход может привести к низкой точности оценки плотности вероятности для "тяжелохвостых" распределений. Поэтому, если существует подозрение о тяжелохвостости распределения, можно провести предварительное усечение выборки (см. раздел 3).
. Стоит, однако, иметь в виду, что такой подход может привести к низкой точности оценки плотности вероятности для "тяжелохвостых" распределений. Поэтому, если существует подозрение о тяжелохвостости распределения, можно провести предварительное усечение выборки (см. раздел 3).
3. Для выбора интервалов (ai, bi], как правило, достаточно использовать разбиение интервала 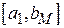 на M равных частей длиной
на M равных частей длиной 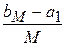 . Тогда:
. Тогда: 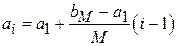 ,
, 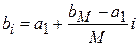 .
.
Ошибку в оценке плотности вероятности можно количественно охарактеризовать, посчитав средний квадрат относительного отклонения оценки 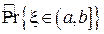 от истинного значения
от истинного значения 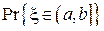 :
:
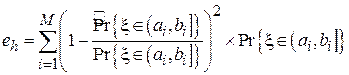
Можно показать, что математическое ожидание величины eh убывает обратно пропорционально объему выборки N: 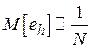 .
.
Дата: 2019-07-24, просмотров: 337.