Одним из способов экспресс-оценки распределения является метод диаграмм Каллена-Фрея. Согласно данному методу, по выборке оцениваются коэффициент асимметрии и коэффициент эксцесса, по которым можно приближенно определить класс распределений, к которому принадлежит выборка.

Коэффициент асимметрии количественно характеризует степень отклонения формы плотности вероятности от симметричной функции:

                                                   ,                                       

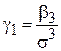где 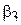 — третий центральный момент,  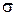— среднеквадратическое отклонение. Легко показать, что для симметричных распределений 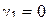. Знак коэффициента асимметрии указывает на перекос распределения вправо или влево относительно математического ожидания

Коэффициент эксцесса — это мера остроты пика распределения случайной величины:

                                                  ,                                      

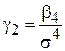где 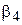 — четвертый центральный момент. Так, для нормального закона распределения случайной величины: 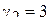. Законы распределения с более острой вершиной, чем у нормального имеют коэффициент эксцесса более 3 и с менее острой вершиной – менее 3. Поэтому иногда используют нормированный коэффициент эксцесса: 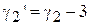. Так, если  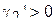пик распределения более заостренный, нежели у нормального закона, если же 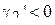, то менее.

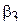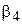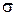Тогда, по выборке оцениваются ,  и  (например, по методу, рассмотренному в Разделе 2), которые после подстановки в выражения (4.6) и (4.7) дают оценки для искомых коэффициентов. Отложив  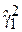и 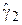 на осях диаграммы Каллена-Фрея можно приближенно оценить, к какому классу распределений принадлежит наблюдаемая выборка (см. рис. 4.4).

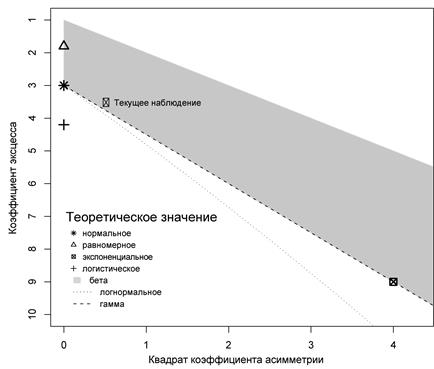
Рис. 4.4. Диаграмма Каллена-Фрея

Вопросы для самопроверки

1. Приведите метод оценки плотности вероятности по выборочным значениям. Каким образом можно оптимизировать данный метод, если известно, что случайная величина имеет дискретное распределение на конечном множестве?

2. Как зависит точность оценки плотности вероятности методом гистограмм от выбранного количества интервалов разбиения? Пояснить данную зависимость.

3. Постройте график теоретической гистограммы для нормального распределения ( 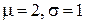) при количестве интервалов равном 5 (см. формулу (4.1)).

4. Постройте график теоретической гистограммы для экспоненциального распределения ( 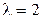) при количестве интервалов равном 21 (см. формулу (4.1)).

5. Постройте график теоретической гистограммы для распределения Лапласа ( 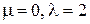) при количестве интервалов равном 41 (см. формулу (4.1)).

6. Поясните принцип, лежащий в основе формулы Стерджеса.

7. В каком случае выбор границ области построения гистограммы как минимума и максимума из элементов выборки является причиной низкой точности оценки? Как этого избежать? Продемонстрировать методом моделирования.

8. Используя свойство распределения Стьюдента, обосновать зависимость математического ожидания 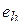 от объема выборки:  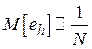(см. подраздел 4.2).

9. Является ли оценка интегральной функции распределения по формуле (4.5) смещенной? Найти величину смещения, если он есть.

10. Как зависит дисперсия оценки интегральной функции распределения по формуле (4.5) от объема выборки?

11. Построить график интегральной функции распределения и плотности вероятности для закона Колмогорова.

12. Как максимальная погрешность в оценке интегральной функции распределения по формуле (4.5) зависит от объема выборки? Обосновать данную зависимость.

13. Подберите распределение, для которого верно следующее: 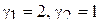. Как изменится вид распределения при изменении различных параметров данного распределения?

14. Каким образом можно оценить коэффициенты асимметрии и эксцесса? Привести пример оценки.

15. Рассчитать для распределения Симпсона с параметрам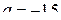и  и 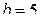 коэффициент асимметрии.

16. Рассчитать для распределения Рэлея с параметрами 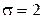 коэффициент эксцесса.

17. Рассчитать для распределения Лапласа с параметрам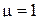и  и 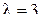 коэффициент асимметрии.

18. Для экспоненциального распределения с параметром 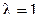 рассчитать коэффициент эксцесса.

19. Для нормального распределения с параметрам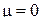и  и 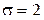 рассчитать коэффициент асимметрии.

20. Для равномерного распределения с параметрами 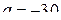 и  рассчитать коэффициент эксцесса.