ЗАДАЧИ И МЕТОДЫ СТАТИСТИЧЕСКОГО ОЦЕНИВАНИЯ
Учебное пособие

Санкт-Петербург
2015
Аннотация
В учебном пособии рассматриваются типовые задачи, возникающие при статистической обработке экспериментальных данных. Основной акцент сделан на задачах выборочного оценивания различных параметров системы случайных величин, отражающих свойства исследуемого объекта. Дается формальное описание наиболее распространенных алгоритмов оценивания таких параметров, например, как моментные и вероятностные характеристики случайной величины, величина сдвига распределения, корреляционные зависимости и т. д. Качество приведенных алгоритмов анализируется при помощи стандартных критериев несмещенности, состоятельности и эффективности. Пособие содержит большое количество примеров использования рассмотренных методов оценивания, а так же индивидуальные задания на закрепление изученного материала.
Оглавление
Введение.. 4
1. Основные определения и понятия математической статистики.. 6
1.1 Предмет математической статистики. 6
1.2 Проведение статистического эксперимента. 7
1.3 Представление случайной величины.. 9
1.4 Свойства оценок. 13
1.4.1 Несмещенность. 13
1.4.2 Состоятельность. 16
1.4.3 Эффективность. 17
1.5 Вопросы для самопроверки. 23
2. Общие методы оценки параметров случайной величины... 25
2.1 Оценка начальных моментов случайной величины.. 25
2.2 Оценка центральных моментов случайной величины.. 27
2.3 Метод моментов. 29
2.4 Метод максимального правдоподобия. 31
2.5 Вопросы для самопроверки. 34
3. Анализ симметричных распределений.. 37
3.1 Квадратичный штраф.. 37
3.2 Симметричные распределения. 38
3.3 Оценки смещения симметричного распределения. 39
3.4 Вопросы для самопроверки. 45
4. Оценка закона распределения случайной величины... 47
4.1 Подходы к оценке закона распределения. 47
4.2 Метод гистограмм.. 47
4.3 Оценка интегральной функции распределения. 51
4.4 Экспресс-оценка закона распределения. 54
4.5 Вопросы для самопроверки. 55
5. Анализ многомерных случайных величин. Построение регрессионных моделей. 57
5.1 Последовательность векторов со случайными и неслучайными компонентами. 57
5.2 Оценка корреляции между компонентами вектора. 58
5.3 Построение полиномиальных регрессий. 62
5.4 Анализ временных рядов. 63
5.5 Вопросы для самопроверки. 67
6. Библиографический список.. 70
Введение
Многие технические, социальные и экономические процессы в мире носят вероятностный характер. Поэтому для широкого круга специалистов важным является приобретение основных знаний в области статистической обработки результатов наблюдений, а также навыков реализации соответствующих алгоритмов на ЭВМ.
Настоящее пособие направлено на закрепление отдельных глав материала, читаемого в курсе «Статистическая обработка информации» для студентов ГУАП. Основной акцент делается на оценивании параметров случайных величин и их систем. Предполагается, что читатель знаком с основами теории вероятности в объеме программы технического ВУЗа.
После освоения очередного раздела предлагается провести самостоятельное исследование с применением ЭВМ для получения практических навыков реализации и анализа рассмотренных алгоритмов. Программы исследований приведены в методических указаниях по выполнению лабораторных работ, выходящих одновременно с настоящим учебным пособием. Не смотря на то, что данные задания не привязаны к конкретной среде программирования, можно порекомендовать применение таких сред компьютерной математики как Octave, Sci-Lab и Matlab.
В пособии принята следующая система обозначений: та информация, на которой авторы хотели бы акцентировать внимание читателя, выделена жирным шрифтом, новые вводимые определения и понятия – курсивом. Случайные величины обозначаются греческими буквами без подстрочных индексов, конкретная реализация случайной величины – соответствующей греческой буквой с индексом, указывающим на номер элемента в выборке. Оценки обозначаются надсимвольным значком ^ (циркумфлекс)[1].
Для более глубокого изучения изложенного материала можно рекомендовать следующую литературу (см. библиографический список в конце пособия):
1. Основные определения и понятия математической статистики
1.1. Предмет математической статистики [1,2]
1.2. Проведение статистического эксперимента [3]
1.3. Представление случайной величины [2, 4]
1.4. Свойства оценок [5]
2. Общие методы оценки параметров случайной величины
2.1. Оценка начальных моментов случайной величины [4]
2.2. Оценка центральных моментов случайной величины [4]
2.3. Метод моментов [3,5]
2.4. Метод максимального правдоподобия [3,5,6]
3. Анализ симметричных распределений [5]
4. Оценка закона распределения случайной величины
4.1. Подходы к оценке закона распределения [2,3,4]
4.2. Метод гистограмм [4, 7]
4.3. Оценка интегральной функции распределения [4, 7]
4.4. Экспресс-оценка закона распределения [8]
5. Анализ многомерных случайных величин. Построение регрессионных моделей.
5.1. Последовательность векторов со случайными и неслучайными компонентами [3, 5]
5.2. Оценка корреляции между компонентами вектора [3, 4, 5]
5.3. Построение полиномиальных регрессий [9]
5.4. Анализ временных рядов [9]
1. Основные определения и понятия математической статистики
Пример 1.
Пусть объектом изучения является лекарственный препарат, а задачей исследования – выяснение его эффективности 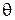 : например, насколько в среднем уменьшается уровень холестерина в крови в случае его приема. Очевидно, что в силу сложности биохимических реакций в организме человека теоретический расчет данной величины едва ли возможен. Тогда прибегают к постановке следующего эксперимента: группе добровольцев замеряют уровень холестерина до приема препарата и после. В данном примере: N соответствует числу пациентов, участвующих в эксперименте,
: например, насколько в среднем уменьшается уровень холестерина в крови в случае его приема. Очевидно, что в силу сложности биохимических реакций в организме человека теоретический расчет данной величины едва ли возможен. Тогда прибегают к постановке следующего эксперимента: группе добровольцев замеряют уровень холестерина до приема препарата и после. В данном примере: N соответствует числу пациентов, участвующих в эксперименте, 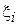 - тому, на сколько ммоль/л уменьшился уровень холестерина у i-го пациента после приема препарата. Можно предложить следующий несложный алгоритм оценивания:
- тому, на сколько ммоль/л уменьшился уровень холестерина у i-го пациента после приема препарата. Можно предложить следующий несложный алгоритм оценивания: 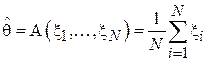 .
.
Пример 2.
Как правило, заказчик информационной системы в техническом задании выдвигает к разработчику требования по быстродействию. Например, требование может быть следующим: время отклика системы на запрос пользователя с высокой вероятностью (например, 0.99) не должно превышать заданного порога h. Тогда 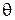 – вероятность того, что время выполнения превысит h. Для того, чтобы доказать соответствие разработки данному требованию формируется N запросов, для каждого из которых регистрируется время выполнения
– вероятность того, что время выполнения превысит h. Для того, чтобы доказать соответствие разработки данному требованию формируется N запросов, для каждого из которых регистрируется время выполнения 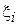 . Тогда простейшим алгоритмом будет
. Тогда простейшим алгоритмом будет 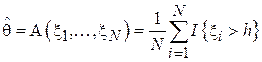 . Здесь
. Здесь 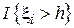 - индикаторная функция, принимающая значение 1, если
- индикаторная функция, принимающая значение 1, если 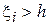 , и 0 иначе.
, и 0 иначе.
При дальнейшем изложении, если не оговорено отдельно, будем полагать, что все эксперименты проводятся при одинаковых условиях и независимо друг от друга. Тогда можно считать, что 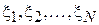 является выборкой независимых, одинаково распределенных случайных величин[2].
является выборкой независимых, одинаково распределенных случайных величин[2].
Зачастую, для оценивания 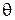 можно предложить сразу несколько алгоритмов (оценок), что приводит к необходимости введения формальных критериев качества их работы. Кратко напомним о способах представления случайных величин, а затем рассмотрим три основных свойства оценок, позволяющие сравнивать их между собой с тем, чтобы выбрать наилучшую.
можно предложить сразу несколько алгоритмов (оценок), что приводит к необходимости введения формальных критериев качества их работы. Кратко напомним о способах представления случайных величин, а затем рассмотрим три основных свойства оценок, позволяющие сравнивать их между собой с тем, чтобы выбрать наилучшую.
Пример 3.
В физической лаборатории анализируются возможные значения кинетической энергии частиц. Однако лабораторная установка позволяет измерять только их скорости 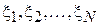 . Тогда
. Тогда 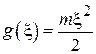 и далее работа идет уже с выборкой
и далее работа идет уже с выборкой 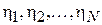 , где
, где 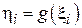 .
.
Введем следующее стандартное обозначение:
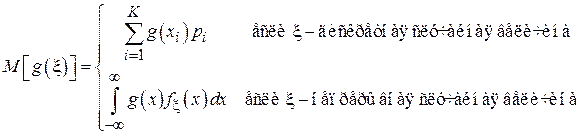
Вычисленная по данной формуле величина 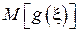 соответствует среднему значению функции
соответствует среднему значению функции 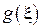 (например, для Примера 1 - средней энергии частицы).
(например, для Примера 1 - средней энергии частицы).
Частичную информацию о случайной величине содержат так называемые моменты. Для большого класса задач является достаточным знание лишь отдельных моментов случайной величины, поэтому важной задачей является их оценка по выборке.
По определению, начальным моментом k -го порядка 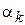 называется следующая величина:
называется следующая величина:
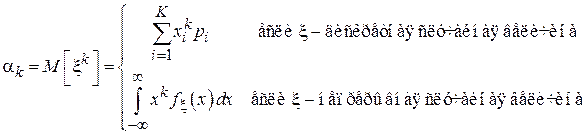 .
.
Таким образом, неформальным определением начального момента является среднее значение случайной величины, возведенной в степень k. Отдельно стоит отметить случай 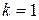 (первый начальный момент). Момент
(первый начальный момент). Момент 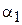 называется математическим ожиданием (МО) случайной величины
называется математическим ожиданием (МО) случайной величины 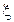 , характеризует ее среднее значение и традиционно обозначается через
, характеризует ее среднее значение и традиционно обозначается через 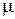 .
.
Центральный момент k -го порядка определяется в выражении (1.6).
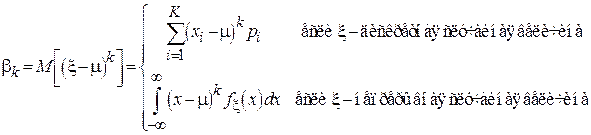 .
.
Центральный момент 2-го порядка 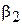 называется дисперсией случайной величины и характеризует меру разброса случайной величины относительно среднего значения. Дисперсия также обозначается через
называется дисперсией случайной величины и характеризует меру разброса случайной величины относительно среднего значения. Дисперсия также обозначается через 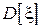 . На практике зачастую удобней работать не с самой дисперсией, а с ее корнем – среднеквадратическим отклонением
. На практике зачастую удобней работать не с самой дисперсией, а с ее корнем – среднеквадратическим отклонением 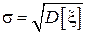 (СКО). Интерпретация других центральных моментов, третьего и четвертого, будет дана в разделе 4.
(СКО). Интерпретация других центральных моментов, третьего и четвертого, будет дана в разделе 4.
Раскрыв скобки в подынтегральном выражении (1.6) и учитывая (1.5) можно получить следующее выражение для центрального момента:
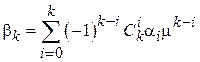
Так, в частности, дисперсия 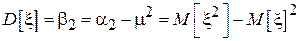 .
.
Замечание. В случае если при вычислении интегралов (1.5)-(1.6) для некоторых k появляется неопределенность, соответствующие моменты случайной величины не существуют. Далее, если не будет оговорено отдельно, везде будем полагать, что рассматриваемые интегралы существуют и являются сходящимися.
Свойства оценок
Несмещенность
Так как оценка является функцией от нескольких случайных величин (элементов выборки), то очевидно, что и сама оценка является случайной величиной. Таким образом, оценка может принимать значение как превышающее истинное, так и, наоборот, заниженное. Естественным желанием является то, чтобы в среднем оценка совпадала с истинным значением, т.е.:
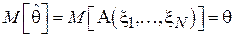 .
.
Такая оценка называется несмещенной. Можно ввести величину 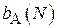 , характеризующую величину смещения, вносимого при использовании алгоритма
, характеризующую величину смещения, вносимого при использовании алгоритма 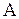 по выборке объема N:
по выборке объема N:
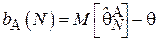
Здесь и далее 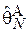 обозначает оценку параметра
обозначает оценку параметра 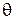 при помощи алгоритма
при помощи алгоритма 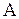 по выборке объема N. Если
по выборке объема N. Если 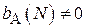 , то оценка является смещенной. Возможны также случаи, когда для конечного N оценка – смещенная, но:
, то оценка является смещенной. Возможны также случаи, когда для конечного N оценка – смещенная, но:
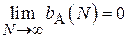 .
.
Данная оценка называется асимптотически несмещенной. Т.е. при достаточно большом объеме выборки N, величиной смещения можно пренебречь.
Пример 4.
При анализе трафика, передаваемого с сервера на компьютеры клиентов, производится оценка среднего размера пакета передаваемого по сети. Для этого из общего потока выбирается N пакетов, размеры которых фиксируются и усредняются. В данном примере случайная величина 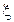 характеризует размер пакета, искомый параметр
характеризует размер пакета, искомый параметр 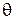 - среднее значение
- среднее значение 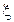 (т.е.
(т.е. 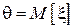 ), элементы выборки
), элементы выборки 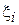 - размеры зарегистрированных пакетов, алгоритм оценивания
- размеры зарегистрированных пакетов, алгоритм оценивания 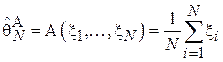 . Проверим, является ли данная оценка смещенной:
. Проверим, является ли данная оценка смещенной:
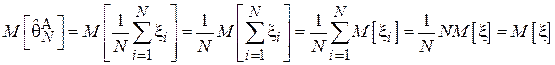
Таким образом, данная оценка является несмещенной.
Пример 5.
Пусть известно, что время отклика базы данных на запрос пользователя является равномерно распределенной случайной величиной в диапазоне 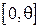 . Задачей исследователя является выяснение величины
. Задачей исследователя является выяснение величины 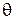 - т.е. худшего случая, при котором задержка максимальна. Применяется следующая оценка:
- т.е. худшего случая, при котором задержка максимальна. Применяется следующая оценка: 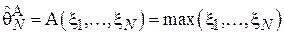 , т.е. максимальная задержка, зарегистрированная в ход проведения эксперимента, состоящего из N запросов. Для упрощения выкладок при проверке смещенности данной оценки введем следующее обозначение для максимального элемента выборки
, т.е. максимальная задержка, зарегистрированная в ход проведения эксперимента, состоящего из N запросов. Для упрощения выкладок при проверке смещенности данной оценки введем следующее обозначение для максимального элемента выборки 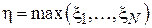 (т.е.
(т.е. 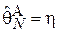 и
и 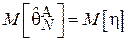 ). Найдем интегральную функцию распределения величины
). Найдем интегральную функцию распределения величины 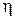 :
:
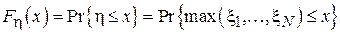
Для того чтобы максимальный элемент выборки не превосходил x, необходимо и достаточно, чтобы каждый элемент выборки не превосходил x. Обратное также верно. Тогда, учитывая независимость случайных величин 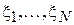 получим:
получим:
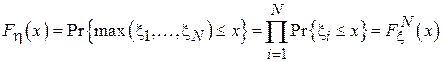
Учитывая, что функция 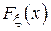 описывает равномерное распределение в диапазоне
описывает равномерное распределение в диапазоне 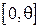 , получим:
, получим:
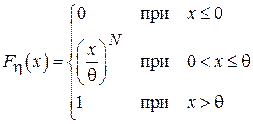 .
.
Воспользовавшись формулой (1.3) получим выражение для плотности вероятности 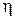 :
:
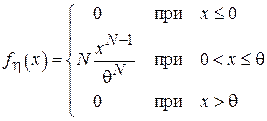 .
.
Тогда:
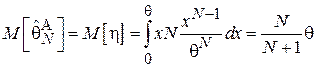
Таким образом, данная оценка является смещенной, причем:
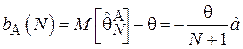
Очевидно, что 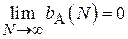 и рассмотренная оценка является асимптотически несмещенной.
и рассмотренная оценка является асимптотически несмещенной.
В тех случаях, когда величина смещения может быть вычислена заранее, смещенная оценка может быть превращена в несмещенную:
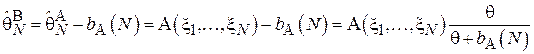
Так, например, для оценки, рассмотренной в Примере 5, несмещенный вариант имеет следующий вид:
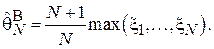
Состоятельность
При обработке выборки исследователь интуитивно предполагает, что, чем больше ее объем, тем ближе будет оценка к истинному значению. Т.е. с ростом N, ошибка в оценивании 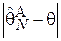 должна стремиться к нулю. Это возможно, если алгоритм оценки эффективно использует ту информацию об искомом параметре, которая содержится в выборке.
должна стремиться к нулю. Это возможно, если алгоритм оценки эффективно использует ту информацию об искомом параметре, которая содержится в выборке.
Формально данное свойство определяется следующим образом: оценка является состоятельной, если 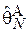 сходится по вероятности к
сходится по вероятности к 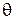 :
:
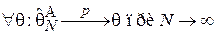 .
.
Сходимость по вероятности в свою очередь означает, что для любого, сколь угодно малого, отличного от нуля 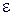 :
:
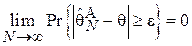
То есть всегда найдется такой объем выборки, который с вероятностью, близкой к единице обеспечит необходимую величину ошибки в оценивании 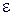 , какой бы малой она не была.
, какой бы малой она не была.
Пример 6.
Рассмотрим оценку из Примера 4 и выясним, является ли она состоятельной. Эта оценка является несмещенной, а, значит, 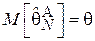 и можно применить второе неравенство Чебышёва:
и можно применить второе неравенство Чебышёва:
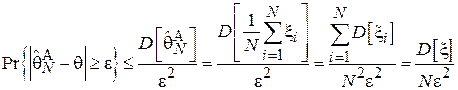 .
.
Очевидно, что при конечной 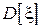 для
для 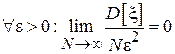 , что доказывает состоятельность рассмотренной оценки.
, что доказывает состоятельность рассмотренной оценки.
При помощи аналогичных рассуждений можно показать, что оценка из Примера 5 также является состоятельной.
Эффективность
Предположим, что для проведения эксперимента перед исследователем стоит выбор одного из двух алгоритмов оценивания искомого параметра системы. Оба алгоритма обеспечивают оценки несмещенные и состоятельные. Как осуществить выбор одного из них? Для ответа на этот вопрос вводят третий параметр оценки – параметр эффективности. Прежде, чем дать формальное определение эффективности, дадим ее качественную интерпретацию. На рис. 1.2 для двух гипотетических оценок приводятся графики зависимости погрешности оценивания от объема выборки. Не смотря на то, что оба алгоритма обеспечивают сколь угодно малую погрешность при 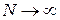 , при конечном N алгоритм 2 явно кажется более предпочтительным, т.е. оценка 2 эффективнее оценки 1.
, при конечном N алгоритм 2 явно кажется более предпочтительным, т.е. оценка 2 эффективнее оценки 1.
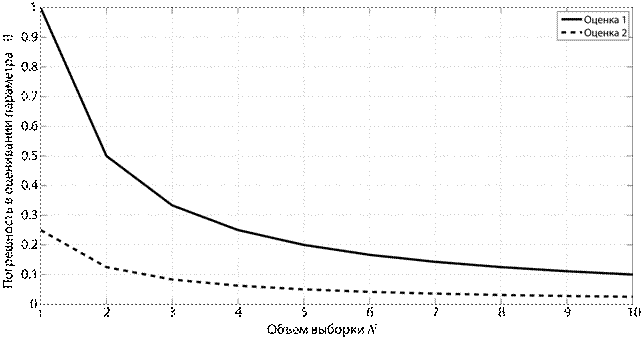
Рис. 1.2. Сравнение двух алгоритмов оценивания
Чтобы количественно измерять эффективность введем несколько вспомогательных функций.
Функцией штрафа 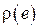 называется функция, характеризующая меру негативных последствий, возникающих при той или иной ошибке e оценивания параметра системы. Как правило, чем больше
называется функция, характеризующая меру негативных последствий, возникающих при той или иной ошибке e оценивания параметра системы. Как правило, чем больше 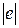 , тем больше значение
, тем больше значение 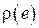 . Функция штрафа выбирается исходя из специфики той предметной области, в которой ведется статистический анализ и может принимать достаточно сложный вид.
. Функция штрафа выбирается исходя из специфики той предметной области, в которой ведется статистический анализ и может принимать достаточно сложный вид.
Пример 7.
По данным Гидрометцентра проводится оценка количества осадков, выпавших в некотором регионе. Из количества осадков рассчитывается тип и объем удобрений, которые необходимо применить на сельскохозяйственном поле. Известно, что неправильно выбранный режим удабривания приводит к падению количества урожая. Тогда, функция штрафа может иметь, например, вид, приведенный на рис. 1.3.
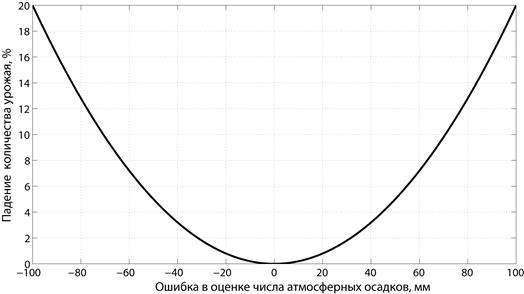
Рис. 1.3. Функция штрафа в Примере 7
Пример 8.
В ходе работы телекоммуникационной системы приемник периодически проводит оценку мощности шумов, присутствующих в канале. Этот уровень учитывается в процессе декодирования принимаемого сообщения. Известно, что ошибочно введенная в декодер информация о шумах повышает вероятность битовой ошибки при приеме данных. При этом заниженная оценка мощности приводит к существенно большему ухудшению качества приема, нежели завышенная. Типичная функция штрафа приведена на рис. 1.4.
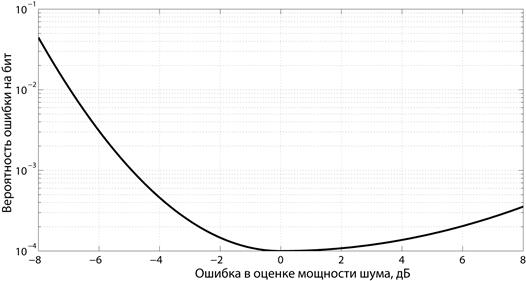
Рис. 1.4. Функция штрафа в Примере 8
Как правило, многие реальные функции штрафа могут быть хорошо аппроксимированы так называемой квадратичной штрафной функцией 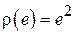 или абсолютной штрафной функцией
или абсолютной штрафной функцией 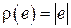 .
.
Оценка параметра является случайной величиной, а, значит, ошибка в оценивании и величина штрафа также являются случайными величинами. Таким образом, вводят функцию риска:
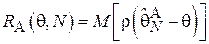 .
.
Т.е. функция риска характеризует средний штраф, который заплатит исследователь при использовании алгоритма 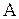 для оценки параметра
для оценки параметра 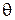 по выборке объема N. Более эффективной является та оценка, которая обеспечивает меньший риск.
по выборке объема N. Более эффективной является та оценка, которая обеспечивает меньший риск.
Заметим, что для несмещенных оценок в случае применения квадратичной штрафной функции:
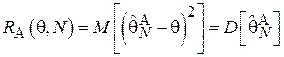
Т.е. функция риска совпадает с дисперсией оценки (см. выражение (1.6)).
Как можно видеть, функция риска зависит как от объема выборки, так и от истинного значения параметра 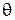 . Таким образом, для различных диапазонов значения
. Таким образом, для различных диапазонов значения 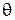 разные оценки могут оказаться более или менее эффективными. При этом ожидается, что для состоятельных оценок
разные оценки могут оказаться более или менее эффективными. При этом ожидается, что для состоятельных оценок 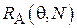 убывает с ростом N. Проиллюстрируем эти зависимости в Примерах 9 и 10.
убывает с ростом N. Проиллюстрируем эти зависимости в Примерах 9 и 10.
Пример 9.
Проводится эксперимент, в ходе которого выясняется вероятность потери пакета 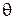 при передаче по вычислительной сети. Для этого по сети передаются N тестовых пакетов, успешный прием или потеря которых регистрируется на приемной стороне. Вводится величина
при передаче по вычислительной сети. Для этого по сети передаются N тестовых пакетов, успешный прием или потеря которых регистрируется на приемной стороне. Вводится величина 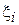 , равная единице, в случае, если i-й пакет оказался утерянным, и нулю иначе. Тогда воспользуемся следующей несложной оценкой:
, равная единице, в случае, если i-й пакет оказался утерянным, и нулю иначе. Тогда воспользуемся следующей несложной оценкой: 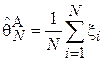 . Найдем выражение
. Найдем выражение 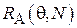 для случая применения квадратичной штрафной функции. Очевидно, что
для случая применения квадратичной штрафной функции. Очевидно, что 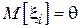 , тогда:
, тогда:
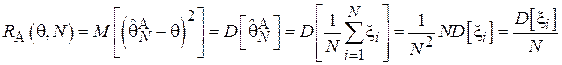
Т.к. 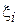 является Бернуллиевской случайной величиной с параметром
является Бернуллиевской случайной величиной с параметром 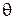 , то:
, то:
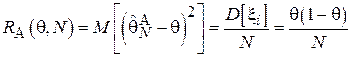 .
.
Пример 10.
Для той же задачи из Примера 9 можно также предложить другую, менее очевидную оценку для 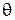 (оценку Лемана-Ходжеса):
(оценку Лемана-Ходжеса):
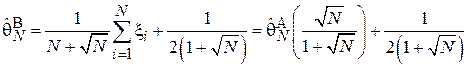
Тогда:
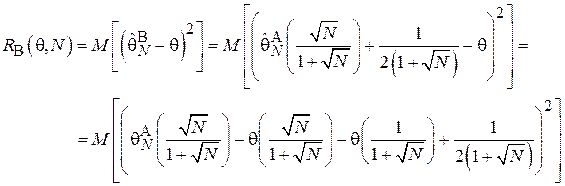
Перегруппировав слагаемые и вынеся константы за знак математического ожидания получим:
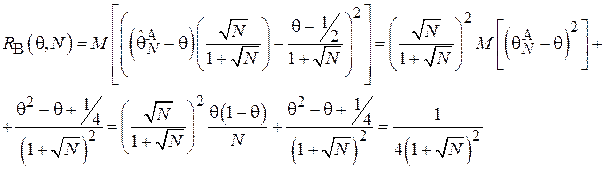
На рис. 1.5 и 1.6 для обеих оценок приведены графики зависимости функций риска от 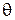 (при N = 10) и от N (при
(при N = 10) и от N (при 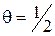 ).
).
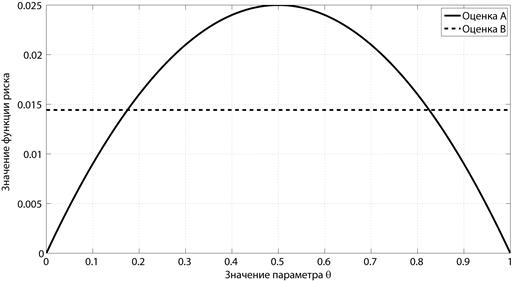
Рис. 1.5 Зависимость риска от значения параметра 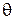 при объеме выборки N = 10 (Примеры 9 и 10)
при объеме выборки N = 10 (Примеры 9 и 10)
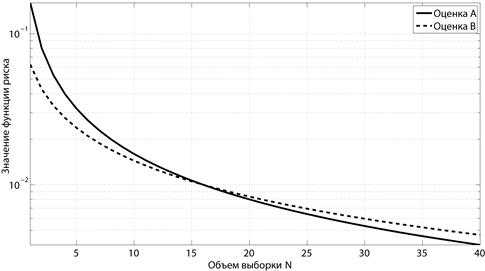
Рис. 1.6 Зависимость риска от объема выборки при значении параметра 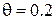 (Примеры 9 и 10)
(Примеры 9 и 10)
Более подробно особенности поведения функции риска будут проанализированы в Разделе 3 на примере оценки смещения симметричного распределения.
Вопросы для самопроверки
1. Выведите формулу для математического ожидания гауссовской случайной величины.
2. Выведите формулу для дисперсии гауссовской случайной величины.
3. Выведите формулу для расчета центрального момента через начальные моменты (см. стр. 10).
4. Как определить вероятность попадания случайной величины в заданный интервал с помощью плотности вероятности и интегральной функции распределения? Привести пример.
5. Какими преобразованиями связаны между собой интегральная и дифференциальная функции распределения? Приведите пример пересчета.
6. Доказать первое неравенство Чебышева. Привести пример его использования.
7. Доказать второе неравенство Чебышева. Привести пример его использования.
8. Является ли 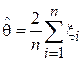 несмещенной оценкой для правой границы диапазона значений равномерно распределенной случайной величины [0,
несмещенной оценкой для правой границы диапазона значений равномерно распределенной случайной величины [0, 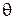 ]? Если оценка окажется смещенной, найти величину смещения (см. Пример 5).
]? Если оценка окажется смещенной, найти величину смещения (см. Пример 5).
9. Является ли 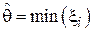 несмещенной оценкой для левой границы диапазона значений равномерно распределенной случайной величины [
несмещенной оценкой для левой границы диапазона значений равномерно распределенной случайной величины [ 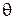 ,5]? Если оценка окажется смещенной, найти величину смещения (см. Пример 5).
,5]? Если оценка окажется смещенной, найти величину смещения (см. Пример 5).
10. Является ли оценки вероятности бернуллиевской случайной величины из Примера 9 смещенной?
11. Является ли оценка Лемана-Ходжеса из Примера 10 смещенной?
12. Поясните смысл понятий «сходимость по вероятности» и «состоятельность».
13. Является ли оценки вероятности бернуллиевской случайной величины из Примера 9 состоятельной.
14. Является ли оценка Лемана-Ходжеса из Примера 10 состоятельной?
15. Проверьте методом моделирования формулу для функции риска оценки вероятности бернуллиевской случайной величины из Примера 9.
16. Проверьте методом моделирования формулу для функции риска оценки Лемана-Ходжеса (см. Пример 10).
17. Предложите оценку параметра N биномиальной случайной величины. Проанализируйте ее смещенность.
18. Предложите оценку параметра N биномиальной случайной величины. Проанализируйте ее состоятельность.
19. Постройте методом моделирования функцию риска для оценки вероятности бернуллиевской случайной величины из Примера 9 при использовании абсолютного штрафа.
20. Постройте методом моделирования функцию риска для оценки вероятности бернуллиевской случайной величины из Примера 10 при использовании абсолютного штрафа.
2. Общие методы оценки параметров случайной величины
Доказательство.
Найдем математическое ожидание выборочного k-го момента:
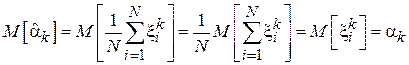 .
.
Свойство 2. Зависимость дисперсии оценки 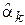 от объема выборки для случая независимых элементов выборки определяется следующим выражением:
от объема выборки для случая независимых элементов выборки определяется следующим выражением:
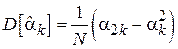
Доказательство.
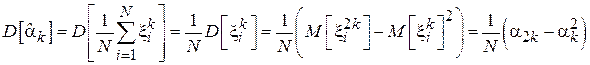
Т.е. дисперсия данной оценки убывает пропорционально объему выборки. Соответственно СКО убывает пропорционально корню из числа элементов в выборке:
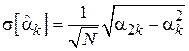
Таким образом, чем больше объем выборки, тем меньше разброс оценки относительно истинного значения момента. Этот вывод находит свое отражение в следующем свойстве.
Свойство 3. Оценка 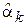 является состоятельной.
является состоятельной.
Доказательство.
По определению свойства состоятельности (см. Раздел 1) необходимо доказать, что:
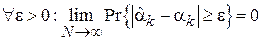 .
.
Из второго неравенства Чебышёва следует, что:
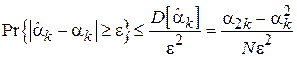
Очевидно, что выражение справа от знака равенства стремится к нулю при 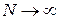 , а, значит, по теореме о двух милиционерах, и вероятность стремится к нулю.
, а, значит, по теореме о двух милиционерах, и вероятность стремится к нулю.
Свойство 4. Оценка 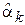 является асимптотически нормальной, т.е.:
является асимптотически нормальной, т.е.:
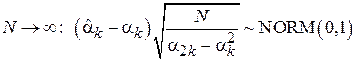 .
.
Доказательство.
Данное свойство следует из центральной предельной теоремы (ЦПТ) и того факта, что 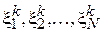 образуют последовательность независимых одинаково распределенных случайных величин.
образуют последовательность независимых одинаково распределенных случайных величин.
Из свойства 4 и закона трех сигма (ЗТС) следует следующее инженерное правило (Свойство 5).
Свойство 5. При достаточно большом объеме выборки N, выход 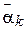 за границы диапазона
за границы диапазона 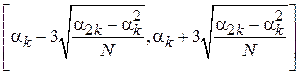 является редким событием.
является редким событием.
Метод моментов
В тех случаях, когда исследователю необходимо провести оценку произвольных параметров случайной величины (например, границ в равномерном распределении или показателя в экспоненциальном) можно воспользоваться достаточно универсальным методом моментов (ММ). Суть метода заключается в следующем. Параметры случайной величины однозначно задают функцию распределения 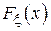 , а, значит, и все моменты распределения. Тогда, если необходимо оценить t параметров
, а, значит, и все моменты распределения. Тогда, если необходимо оценить t параметров 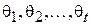 , можно составить следующую систему из t уравнений[3]:
, можно составить следующую систему из t уравнений[3]:
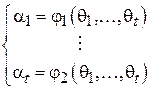
Переразрешив данную систему относительно 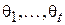 , получим новую систему уравнений, позволяющую найти параметры распределения через его моменты:
, получим новую систему уравнений, позволяющую найти параметры распределения через его моменты:
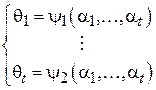
После оценки моментов (например, методами, описанными в подразделах 2.1-2.2) и подстановки их в систему (2.8) получим оценки для искомых параметров распределения.
Пример 11.
Оператор сотовой сети анализирует интервалы времени между звонками, осуществляемыми абонентами. Известно, что эти интервалы распределены по закону, близкому к экспоненциальному. Плотность вероятности для такой случайной величины записывается следующим образом:
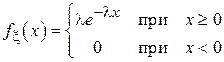 .
.
Тогда искомым будет параметр 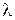 . Подставив выражение для плотности вероятности в формулу (1.5) при k = 1 получим систему (2.8):
. Подставив выражение для плотности вероятности в формулу (1.5) при k = 1 получим систему (2.8):
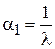 .
.
Тривиальное переразрешение дает следующую систему (2.9):
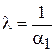 .
.
Подставив в данное выражение формулу (2.1) для оценки первого начального момента получим следующую оценку параметра 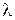 :
:
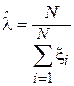 .
.
Здесь 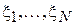 - интервалы времени между звонками, наблюдаемые в процессе работы сети.
- интервалы времени между звонками, наблюдаемые в процессе работы сети.
Пример 12.
По выборке равномерно распределенных случайных величин необходимо одновременно оценить оба параметра данного распределения (левую границу a и правую границу b). Известно, что:
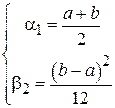 .
.
Решив данную систему относительно a и b получим:
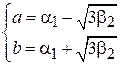 .
.
Оценив по выборке 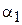 и
и 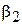 и, подставив их в данную систему, получим оценки по ММ для a и b.
и, подставив их в данную систему, получим оценки по ММ для a и b.
Очевидным недостатком данного метода является сложность переразрешения системы (2.8) в систему (2.9) для некоторых распределений, а также невысокая точность в случае одновременного оценивания большого количества параметров.
Пример 13.
Известно, что ошибка определения координаты посредством GPS имеет распределение, близкое к распределению Лапласа, плотность которого описывается следующим выражением:
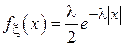 .
.
Из анализа выражения видно, что точность GPS приемника будет определяться параметром распределения 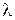 (чем
(чем 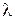 больше, тем точнее работа приемника). Для оценки этого параметра GPS устанавливают в точке, координата которой известна точно и N раз измеряют эту координату, регистрируя каждый раз величину ошибки
больше, тем точнее работа приемника). Для оценки этого параметра GPS устанавливают в точке, координата которой известна точно и N раз измеряют эту координату, регистрируя каждый раз величину ошибки 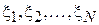 . Оценим по этой выборке параметр
. Оценим по этой выборке параметр 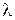 с помощью ММП в форме (2.11).
с помощью ММП в форме (2.11).
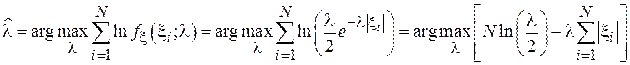
Взяв от выражения правдоподобия производную и приравняв ее к нулю получим:
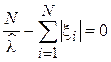 .
.
Тогда оценка по ММП примет следующий вид:
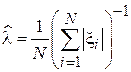 .
.
Пример 14.
В теории надежности широко используется модель, согласно которой время наработки технического устройства до отказа (т.е. время, проходящее с момента начал эксплуатации устройства до момента его поломки) описывается случайной величиной, имеющей распределение Вейбулла:
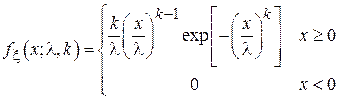
Это распределение – двухпараметрическое с параметрами k (коэффициент формы) и 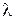 (коэффициент масштаба). Условно можно сказать, что значение параметра k говорит в основном о характере отказов устройства[4], параметр
(коэффициент масштаба). Условно можно сказать, что значение параметра k говорит в основном о характере отказов устройства[4], параметр 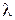 - о среднем сроке эксплуатации. Для оценки значений данных параметров для нового типа устройства изготавливают опытную партию, для каждого элемента которой регистрируют время наработки до отказа
- о среднем сроке эксплуатации. Для оценки значений данных параметров для нового типа устройства изготавливают опытную партию, для каждого элемента которой регистрируют время наработки до отказа 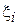 (
( 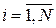 ). Найдем параметры данного распределения по ММП:
). Найдем параметры данного распределения по ММП:
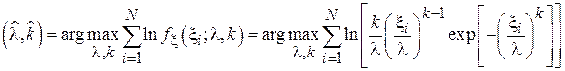
Разложив логарифм произведения в сумму получим:
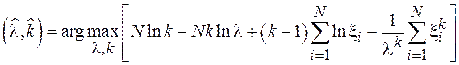
Найдем градиент функции правдоподобия и приравняем его к нулю:
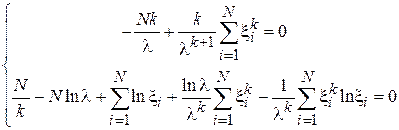 .
.
Из первого уравнения получим:
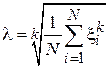 .
.
Подставив данное выражение во второе уравнение и заметив, что 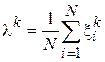 , получим систему в следующем виде:
, получим систему в следующем виде:
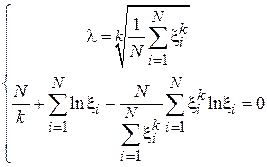 .
.
Перегруппировав слагаемые получим:
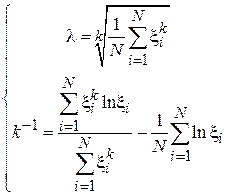 .
.
Численно решив второе уравнение и подставив полученную оценку параметра k в первое уравнение, получим пару оценок 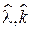 по ММП.
по ММП.
Очевидным недостатком метода максимального правдоподобия является необходимость отыскания максимума от достаточно сложной функции (как, например, в примере 14), что зачастую приходится делать численно.
Вопросы для самопроверки
1. В чем суть центральной предельной теоремы и как она находит свое отражение при нахождении выборочных моментов?
2. Докажите, что оценка дисперсии, приведенная в выражении (2.6), является несмещенной.
3. Как зависит средний квадрат ошибки оценивания момента случайно величины от объема выборки? Почему?
4. В чем состоит закон «трёх сигма»? Продемонстрируйте его на графиках плотности вероятности и интегральной функции распределения.
5. Разработайте моделирующую программу для нахождения вероятности того, что ошибка оценивания превысит заданную величину. Проведите серию вычислительных экспериментов и сопоставьте результаты моделирования с неравенствами Чебышева.
6. Почему график зависимости дисперсии оценки, выполненной по формулам (2.1) и (2.4), от объема выборки, построенный в логарифмическом масштабе, представляет собой прямую линию?
7. Как связаны биномиальное распределение с распределением Бернулли?
8. Доказать, что оценка начального момента (2.1) является несмещенной.
9. Вывести формулу зависимости дисперсии оценки 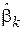 от объема выборки.
от объема выборки.
10. Доказать, что оценка 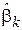 , определяемая выражением (2.4), является состоятельной.
, определяемая выражением (2.4), является состоятельной.
11. Доказать, что оценка 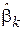 , определяемая выражением (2.4), является асимптотически нормальной.
, определяемая выражением (2.4), является асимптотически нормальной.
12. Методом моделирования проведите исследование эффективности оценки параметра 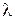 экспоненциального распределения по методу моментов (см. Пример 11).
экспоненциального распределения по методу моментов (см. Пример 11).
13. Методом моделирования проведите исследование эффективности оценки параметров a и b равномерного распределения по методу моментов (см. Пример 12).
14. Выведите выражение для оценки параметра 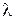 распределения Лапласа по методу моментов (см. Пример 13).
распределения Лапласа по методу моментов (см. Пример 13).
15. Сформулируйте и реализуйте вычислительную процедуру для нахождения параметров k и 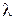 распределения Вейбулла по методу моментов.
распределения Вейбулла по методу моментов.
16. Вывести выражение для оценки математического ожидания гауссовской случайной величины по методу максимального правдоподобия.
17. Вывести выражение для оценки дисперсии гауссовской случайной величины по методу максимального правдоподобия.
18. Вывести выражение для оценки параметра p биномиального распределения по методу максимального правдоподобия.
19. Вывести выражение для оценки параметра N биномиального распределения по методу максимального правдоподобия.
20. Вывести выражение для оценки параметров a и b равномерного распределения по методу максимального правдоподобия.
3. Анализ симметричных распределений
Квадратичный штраф
Как говорилось ранее, для количественного измерения эффективности оценки необходимо выбрать функцию штрафа 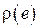 , т.е. меру негативного эффекта, возникающего при той или иной ошибке оценивания
, т.е. меру негативного эффекта, возникающего при той или иной ошибке оценивания 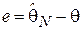 (здесь
(здесь 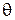 - истинное значение оцениваемого параметра распределения,
- истинное значение оцениваемого параметра распределения, 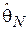 - оценка параметра по выборке объема N).
- оценка параметра по выборке объема N).
Наиболее распространенной функцией является квадратичный штраф, т.е.:
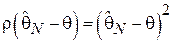
При этом функция риска (т.е. средний штраф, характеризующий точность оценки) записывается следующим образом:
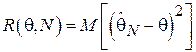 .
.
Чем меньше значение функции риска, тем более эффективной является оценка. Как видно из выражения (3.2), если оценка 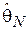 является несмещенной и
является несмещенной и 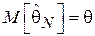 , то функция риска совпадает с дисперсией оценки:
, то функция риска совпадает с дисперсией оценки:
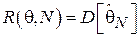 .
.
Так, например, для оценки математического ожидания методом выборочного среднего (см. подразделы 2.2 и 2.3):
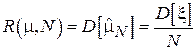 .
.
Симметричные распределения
В данном разделе сравнение эффективности оценок будет иллюстрироваться при помощи симметричных распределений. Будем называть распределение случайной величины 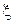 симметричным, если для него существует такое c, что для
симметричным, если для него существует такое c, что для 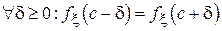 . Очевидно, что при этом число c будет являться центром симметрии плотности вероятности или смещением распределения относительно начала координат. Как правило, смещение соответствует медиане симметричного распределения (в случае, если медиана может быть однозначно определена) и/или математическому ожиданию (в случае существования первого начального момента). На рис. 3.1 приведены примеры симметричных распределений: равномерного, нормального, биномиального и распределения Лапласа.
. Очевидно, что при этом число c будет являться центром симметрии плотности вероятности или смещением распределения относительно начала координат. Как правило, смещение соответствует медиане симметричного распределения (в случае, если медиана может быть однозначно определена) и/или математическому ожиданию (в случае существования первого начального момента). На рис. 3.1 приведены примеры симметричных распределений: равномерного, нормального, биномиального и распределения Лапласа.
Существует ряд задач, для решения которых необходимо оценивание смещения симметричного распределения. Примером может служить сравнение качества деталей, изготовленных по двум различным методикам. Сравнение можно производить путем оценки погрешности изготовления, т.е. анализа случайных величин 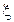 и
и 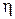 , характеризующих погрешность изготовления детали по 1-й и 2-й методике соответственно.
, характеризующих погрешность изготовления детали по 1-й и 2-й методике соответственно.
Для определения погрешности рассмотрим процесс изготовления детали по двум разным методикам. Пусть: 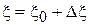 , где
, где 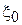 - постоянная величина погрешности, обусловленная методикой изготовления,
- постоянная величина погрешности, обусловленная методикой изготовления, 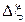 - случайная величина погрешности, обусловленная не зависящими от методики факторами. Аналогично
- случайная величина погрешности, обусловленная не зависящими от методики факторами. Аналогично 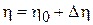 . Будем считать, что
. Будем считать, что 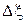 и
и 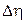 являются независимыми одинаково распределенными случайными величинами с плотностью вероятности
являются независимыми одинаково распределенными случайными величинами с плотностью вероятности 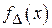 . Введем величину
. Введем величину 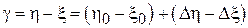 . Известно, что, если две случайные величины (в данном случае
. Известно, что, если две случайные величины (в данном случае 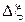 и
и 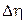 ) – независимы и одинаково распределены, то их разница имеет симметричное распределение с нулевым смещением, определяемое следующим выражением:
) – независимы и одинаково распределены, то их разница имеет симметричное распределение с нулевым смещением, определяемое следующим выражением:
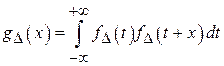
Таким образом, случайная величина 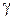 будет характеризоваться симметричной плотностью вероятности
будет характеризоваться симметричной плотностью вероятности 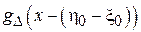 со смещением
со смещением 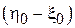 относительно нуля. Если смещение имеет положительный знак (
относительно нуля. Если смещение имеет положительный знак ( 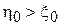 ), то первая методика позволяет выпускать более качественные детали, чем вторая и наоборот.
), то первая методика позволяет выпускать более качественные детали, чем вторая и наоборот.
Для оценки величины смещения изготавливаются две партии деталей, для которых измеренные величины погрешности записываются через 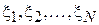 и
и 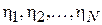 . Тогда можно составить выборку разностей
. Тогда можно составить выборку разностей 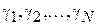 , где
, где 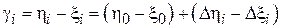 . Далее возникает задача оценки по выборке симметрично распределенных случайных величин
. Далее возникает задача оценки по выборке симметрично распределенных случайных величин 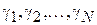 величины их смещения
величины их смещения 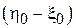 .
.
Выборочное среднее.
Выборочное среднее является простейшей оценкой смещения случайной величины:
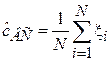 .
.
Данный тип оценки был подробно рассмотрен в предыдущем разделе. Здесь отметим, что в случае, если дисперсия случайной величины равна бесконечности, скорость сходимости оценки к истинному значению может быть существенно медленнее, чем 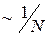 , определяемое в Свойствах 2-3 Раздела 2.1. В случае же, если не существует математическое ожидание, выборочное среднее является несостоятельной оценкой смещения симметричного распределения и не применимо в принципе.
, определяемое в Свойствах 2-3 Раздела 2.1. В случае же, если не существует математическое ожидание, выборочное среднее является несостоятельной оценкой смещения симметричного распределения и не применимо в принципе.
В частности, это справедливо для так называемых "тяжелохвостных" распределений, пример одного из которых (распределения Коши) приведен на рис. 3.2. На графике видно, что, не смотря на кажущуюся схожесть, плотность вероятности Коши имеет одно важное отличие от нормальной плотности, а именно существенно более медленную скорость спадания "хвостов" (обведено на рисунке).
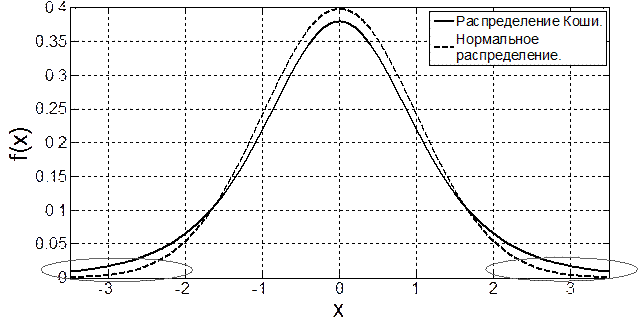
Рис. 3.2. Сравнение распределения Коши и нормального распределения
Таким образом, случайная величина, распределенная по закону Коши, с высокой вероятностью принимает значения, существенно отклоняющиеся от точки смещения. Эти большие значения (выбросы) сильно искажают результирующую сумму (3.3) и делают оценку несостоятельной. Данный негативный эффект может быть частично устранен при помощи метода усечения выборки.
Усеченное среднее.
Основной идеей данного метода является предварительное удаление из выборки т.н. выбросов, сильно отклоняющихся от центра распределения величин. Для этого элементы выборки вначале упорядочиваются в порядке возрастания. Получившаяся в результате последовательность 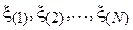 называется вектором порядковых статистик, а ее i-й элемент
называется вектором порядковых статистик, а ее i-й элемент 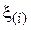 – i -й порядковой статистикой. После этого из выборки удаляются kN первых и kN последних элементов, а от оставшихся считается среднеарифметическое:
– i -й порядковой статистикой. После этого из выборки удаляются kN первых и kN последних элементов, а от оставшихся считается среднеарифметическое:
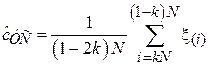
Доля удаляемых элементов k называется коэффициентом усечения и обычно выбирается в диапазоне 0.05-0.2. Чем больше величина k, тем устойчивее оценка к наличию выбросов в выборке, но тем меньше ее эффективность в случае, когда выборка выбросов не содержит. Классическим примером использования усеченного среднего является подсчет среднего балла на спортивных соревнованиях: из выставленных судьями оценок отбрасывается самая маленькая и самая большая оценки. Таким образом, организаторы соревнований борются с намеренным занижением или завышением балла в случае ангажированности судей.
Предельным случаем усеченного среднего, когда из вектора порядковых статистик удалены все элементы кроме центрального, называется метод выборочной медианы.
Выборочная медиана.
Выборочная медиана получается путем отбрасывания из вектора порядковых статистик всех элементов, кроме центрального (в случае, если N – нечетное), либо двух центральных (если N – четное):
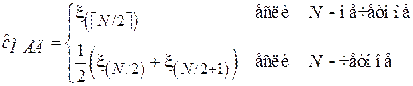 .
.
Здесь символ 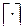 обозначает округление вверх до ближайшего целого. Выборочная медиана является одной из наиболее устойчивых к выбросам оценок, однако неприменима в случае, когда медиана исходного распределения
обозначает округление вверх до ближайшего целого. Выборочная медиана является одной из наиболее устойчивых к выбросам оценок, однако неприменима в случае, когда медиана исходного распределения 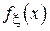 не может быть однозначно определена (т.е. когда
не может быть однозначно определена (т.е. когда 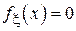 в окрестности точки смещения c).
в окрестности точки смещения c).
Середина размаха.
В случае, когда известно, что распределение элементов выборки 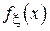 задано на ограниченном интервале, хорошие результаты может давать следующая оценка смещения c:
задано на ограниченном интервале, хорошие результаты может давать следующая оценка смещения c:
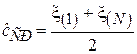 ,
,
т. е. среднеарифметическое значение минимального и максимального элементов выборки. Однако, если 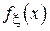 отлична от нуля на бесконечном интервале, в большинстве случаев оценка окажется несостоятельной.
отлична от нуля на бесконечном интервале, в большинстве случаев оценка окажется несостоятельной.
Далее, в таблице 3.1 приведена сводная информация по 4-м рассмотренным оценкам параметра смещения случайной величины с симметричным распределением.
Таблица 3.1 – Сводная информация по методам оценки смещения
| Название метода | Формула оценки | Область применения | Дисперсия оценки |
| Выборочное среднее | 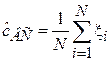
| Оценка является состоятельной при существовании первого начального момента. Указанная дисперсия гарантируется при существовании второго центрального момента. | 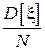
|
| Усеченное среднее[5] | 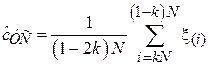
| Применима для широкого класса распределений. | 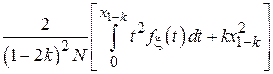
|
| Выборочная медиана | 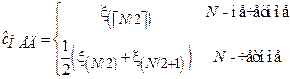
| Оценка является состоятельной с указанной дисперсией при однозначности определения медианы распределения и конечности 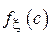 . .
| 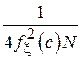
|
| Середина размаха | 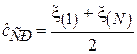
| Оценка является состоятельной при ограниченности области определения случайной величины. | 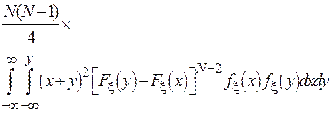
|
Вопросы для самопроверки
1. В каком случае медиана распределения не может быть однозначно определена? Приведите пример.
2. Почему график зависимости дисперсии оценки от объема выборки, построенный в логарифмическом масштабе, представляет собой прямую линию?
3. Для заданного распределения проверьте зависимость среднего квадрата ошибки оценки смещения по выборочному среднему от объема выборки с помощью теоретического выражения (см. таблицу 3.1).
4. Для заданного распределения проверьте зависимость среднего квадрата ошибки оценки смещения по выборочной медиане от объема выборки с помощью теоретического выражения (см. таблицу 3.1).
5. Для заданного распределения проверьте зависимость среднего квадрата ошибки оценки смещения по усеченному среднему от объема выборки с помощью теоретического выражения (см. таблицу 3.1).
6. Вывести формулу дисперсии оценки смещения биномиального распределения 2-го порядка по середине размаха.
7. Предложите свою оценку смещения и проведите ее исследование методом моделирования.
8. Доказать, что у распределения Коши не существует математического ожидания.
9. Доказать, что у распределения Коши второй начальный момент равен бесконечности.
10. Для заданного распределения теоретически сравнить эффективность двух оценок – выборочного среднего и выборочной медианы.
11. Вывести выражение для 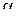 -квантиля экспоненциального распределения.
-квантиля экспоненциального распределения.
12. Вывести выражение для 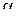 -квантиля равномерного распределения.
-квантиля равномерного распределения.
13. Доказать, что разница независимых одинаково распределенных случайных величин имеет симметричное распределение.
14. Дано:
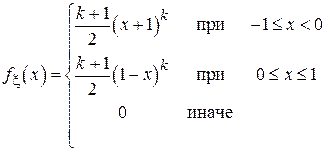
Сравните теоретически эффективности оценок смещения для данного распределения по выборочной медиане и по середине размаха для k = 1.
15. Как зависит эффективность оценки смещения для данного распределения по выборочной медиане от параметра k (см. вопрос 14)?
16. Как зависит эффективность оценки смещения для данного распределения по середине размаха от параметра k (см. вопрос 14)?
17. Выведите выражение для плотности вероятности разности двух независимых случайных величин, распределенных по равномерному закону с параметрами a и b.
18. Выведите выражение для ряда распределения двух независимых случайных величин, распределенных по биномиальному закону с параметрами N и p.
19. Выведите выражение для плотности вероятности разности двух независимых случайных величин, распределенных по экспоненциальному закону с параметром 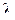 .
.
20. Выведите выражение для плотности вероятности разности двух независимых случайных величин, распределенных по гауссовскому закону с параметрами 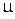 и
и 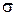 .
.
4. Оценка закона распределения случайной величины
Метод гистограмм
В основе метода гистограмм лежит идея об аппроксимации плотности вероятности 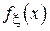 при помощи ступенчатой функции по следующему принципу.
при помощи ступенчатой функции по следующему принципу.
Известно, что вероятность попадания случайной величины в заданный интервал [a, b] находится из следующего выражения:
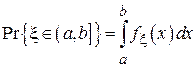
При малой длине (a, b] функцию 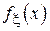 можно считать на этом интервале почти постоянной и можно воспользоваться следующим приближением:
можно считать на этом интервале почти постоянной и можно воспользоваться следующим приближением:
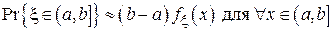 .
.
Тогда:
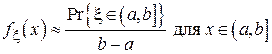 .
.
Соответственно можно разбить область определения случайной величины 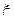 на M непересекающихся интервалов
на M непересекающихся интервалов 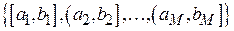 и на каждом интервале аппроксимировать плотность вероятности при помощи выражения (4.1). Очевидно, что чем больше M и меньше длительности интервалов
и на каждом интервале аппроксимировать плотность вероятности при помощи выражения (4.1). Очевидно, что чем больше M и меньше длительности интервалов 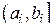 , тем более точной будет аппроксимация (см., например, рис. 4.1, на котором приведены аппроксимации плотности распределения закона Симпсона при M = 11 и M = 31).
, тем более точной будет аппроксимация (см., например, рис. 4.1, на котором приведены аппроксимации плотности распределения закона Симпсона при M = 11 и M = 31).
а) 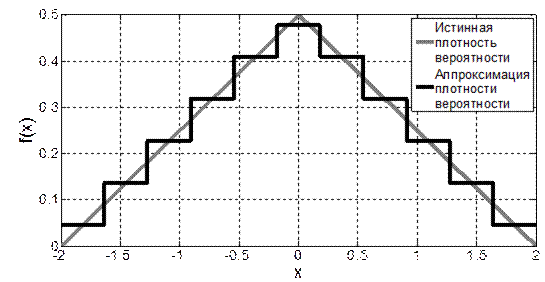
б)
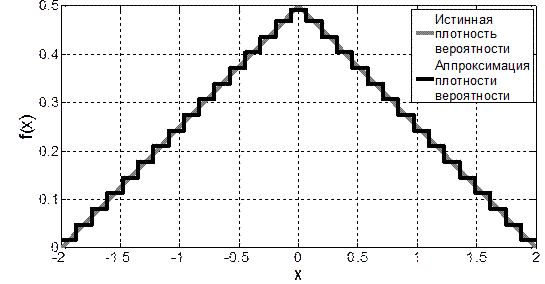
Рис. 4.1. Графики аппроксимации ПВ закона Симпсона при М=11 и M =31
По выборке можно осуществить оценку 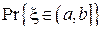 следующим образом:
следующим образом:
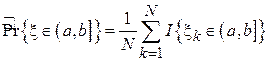 ,
,
где N – объем выборки, 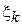 - k-й элемент выборки,
- k-й элемент выборки, 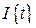 - индикатор события t. Тогда оценка плотности вероятности будет иметь следующий вид:
- индикатор события t. Тогда оценка плотности вероятности будет иметь следующий вид:
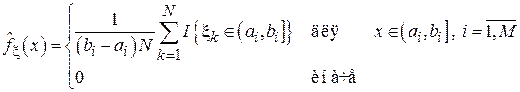
Графическое изображение функции (4.3) называется гистограммой и имеет характерный ступенчатый вид (см., например, рис. 4.2). Очевидно, что гистограмма будет задана на интервале [a1, bM].
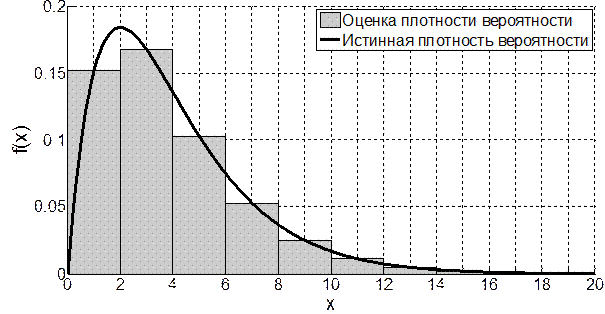
Рис. 4.2. График плотности распределения хи-квадрат и построенной гистограммы
Для применения выражения (4.3) приходится решать ряд практических вопросов, таких, например, как оценка области определения случайной величины, выбор числа интервалов M, границы интервалов (ai, bi] и т. д. Ниже приведем некоторые стандартные рекомендации.
1. Число интервалов разбиения выбирать исходя из правила Стерджеса: 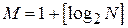 , где N – объем выборки,
, где N – объем выборки, 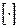 – знак округления.
– знак округления.
2. В некоторых источниках можно встретить следующую рекомендацию к выбору границ области построения гистограммы: 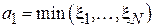 ,
, 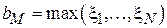 . Стоит, однако, иметь в виду, что такой подход может привести к низкой точности оценки плотности вероятности для "тяжелохвостых" распределений. Поэтому, если существует подозрение о тяжелохвостости распределения, можно провести предварительное усечение выборки (см. раздел 3).
. Стоит, однако, иметь в виду, что такой подход может привести к низкой точности оценки плотности вероятности для "тяжелохвостых" распределений. Поэтому, если существует подозрение о тяжелохвостости распределения, можно провести предварительное усечение выборки (см. раздел 3).
3. Для выбора интервалов (ai, bi], как правило, достаточно использовать разбиение интервала 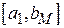 на M равных частей длиной
на M равных частей длиной 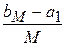 . Тогда:
. Тогда: 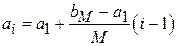 ,
, 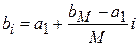 .
.
Ошибку в оценке плотности вероятности можно количественно охарактеризовать, посчитав средний квадрат относительного отклонения оценки 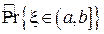 от истинного значения
от истинного значения 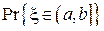 :
:
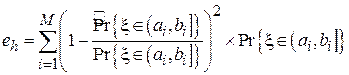
Можно показать, что математическое ожидание величины eh убывает обратно пропорционально объему выборки N: 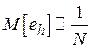 .
.
Теорема Гливенко-Кантелли.
Пусть 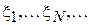 - бесконечная последовательность из чисел, распределенных согласно функции
- бесконечная последовательность из чисел, распределенных согласно функции 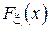 . Пусть
. Пусть 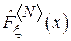 - эмпирическая интегральная функция распределения, построенная по первым N элементам выборки. Тогда:
- эмпирическая интегральная функция распределения, построенная по первым N элементам выборки. Тогда:
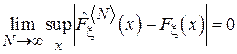 .
.
Здесь 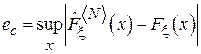 обозначает точную верхнюю грань[6] для ошибки в оценке. Таким образом, эмпирическая интегральная функция распределения является состоятельной оценкой интегральной функции распределения.
обозначает точную верхнюю грань[6] для ошибки в оценке. Таким образом, эмпирическая интегральная функция распределения является состоятельной оценкой интегральной функции распределения.
Теорема Колмогорова.
Скорость сходимости функции 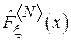 к
к 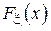 определяется из следующего выражения:
определяется из следующего выражения:
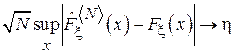 при
при 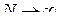
Здесь 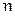 - случайная величина, распределенная по закону Колмогорова:
- случайная величина, распределенная по закону Колмогорова:
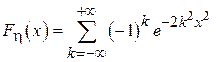
Т. е. максимальная погрешность в оценке в среднем убывает обратно пропорционально корню из объема выборки: 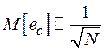 (ср. с выражениями (2.3) и (2.5)).
(ср. с выражениями (2.3) и (2.5)).
Вопросы для самопроверки
1. Приведите метод оценки плотности вероятности по выборочным значениям. Каким образом можно оптимизировать данный метод, если известно, что случайная величина имеет дискретное распределение на конечном множестве?
2. Как зависит точность оценки плотности вероятности методом гистограмм от выбранного количества интервалов разбиения? Пояснить данную зависимость.
3. Постройте график теоретической гистограммы для нормального распределения ( 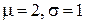 ) при количестве интервалов равном 5 (см. формулу (4.1)).
) при количестве интервалов равном 5 (см. формулу (4.1)).
4. Постройте график теоретической гистограммы для экспоненциального распределения ( 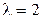 ) при количестве интервалов равном 21 (см. формулу (4.1)).
) при количестве интервалов равном 21 (см. формулу (4.1)).
5. Постройте график теоретической гистограммы для распределения Лапласа ( 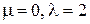 ) при количестве интервалов равном 41 (см. формулу (4.1)).
) при количестве интервалов равном 41 (см. формулу (4.1)).
6. Поясните принцип, лежащий в основе формулы Стерджеса.
7. В каком случае выбор границ области построения гистограммы как минимума и максимума из элементов выборки является причиной низкой точности оценки? Как этого избежать? Продемонстрировать методом моделирования.
8. Используя свойство распределения Стьюдента, обосновать зависимость математического ожидания 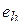 от объема выборки:
от объема выборки: 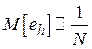 (см. подраздел 4.2).
(см. подраздел 4.2).
9. Является ли оценка интегральной функции распределения по формуле (4.5) смещенной? Найти величину смещения, если он есть.
10. Как зависит дисперсия оценки интегральной функции распределения по формуле (4.5) от объема выборки?
11. Построить график интегральной функции распределения и плотности вероятности для закона Колмогорова.
12. Как максимальная погрешность в оценке интегральной функции распределения по формуле (4.5) зависит от объема выборки? Обосновать данную зависимость.
13. Подберите распределение, для которого верно следующее: 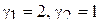 . Как изменится вид распределения при изменении различных параметров данного распределения?
. Как изменится вид распределения при изменении различных параметров данного распределения?
14. Каким образом можно оценить коэффициенты асимметрии и эксцесса? Привести пример оценки.
15. Рассчитать для распределения Симпсона с параметрами 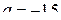 и
и 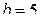 коэффициент асимметрии.
коэффициент асимметрии.
16. Рассчитать для распределения Рэлея с параметрами 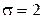 коэффициент эксцесса.
коэффициент эксцесса.
17. Рассчитать для распределения Лапласа с параметрами 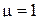 и
и 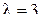 коэффициент асимметрии.
коэффициент асимметрии.
18. Для экспоненциального распределения с параметром 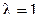 рассчитать коэффициент эксцесса.
рассчитать коэффициент эксцесса.
19. Для нормального распределения с параметрами 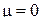 и
и 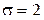 рассчитать коэффициент асимметрии.
рассчитать коэффициент асимметрии.
20. Для равномерного распределения с параметрами 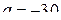 и
и  рассчитать коэффициент эксцесса.
рассчитать коэффициент эксцесса.
Пример 15.
В ходе социологического опроса респонденту предлагается заполнить анкету, содержащую K вопросов. Экспериментальная выборка соответствует результатам опроса N участников. Каждый элемент выборки 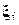 будет содержать K компонентов, соответствующих ответам на соответствующие вопросы i-го респондента:
будет содержать K компонентов, соответствующих ответам на соответствующие вопросы i-го респондента: 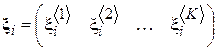 .
.
Пример 16.
Пациент, находящийся под наблюдением врачей, периодически посещает поликлинику для сдачи анализа крови. Дата посещения определяется расписанием работы лаборатории и личным временем пациента. Тогда, по итогам N посещений будет сформирована выборка 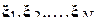 , каждый элемент которой имеет вид
, каждый элемент которой имеет вид 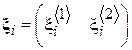 , где
, где 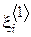 - дата i-го посещения,
- дата i-го посещения, 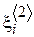 - результаты анализа в этот день.
- результаты анализа в этот день.
Пример 17.
На сайте Bloomberg ежедневно обновляется информация о текущих котировках валют, акций, цветных металлов и пр. При анализе динамики цен на интересующий исследователя ресурс, формируется подборка информации за последние N дней 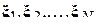 , в которой
, в которой 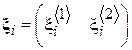 . Здесь
. Здесь 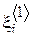 - дата, за которую запрашивается информация (вообще говоря, величина не случайная),
- дата, за которую запрашивается информация (вообще говоря, величина не случайная), 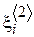 - цена ресурса в этот день.
- цена ресурса в этот день.
Пример 18.
В ходе эксперимента, у случайно выбранного участника регистрируют рост 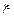 и вес
и вес 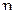 . Очевидно, что
. Очевидно, что 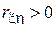 .
.
Пример 19.
В ходе испытания мобильной сети, в случайных точках города производится замер расстояния до ближайшей базовой станции 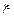 и максимальной скорости приема данных
и максимальной скорости приема данных 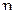 . В силу того, что с ростом расстояния сигнал ослабевает и скорость падает,
. В силу того, что с ростом расстояния сигнал ослабевает и скорость падает, 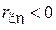 .
.
Замечание.
Так как коррелированность – это всего лишь один из возможных типов зависимости, из некоррелированности ( 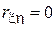 ), вообще говоря, не следует независимости случайных величин.
), вообще говоря, не следует независимости случайных величин.
Одним из стандартных способов оценивания 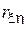 по выборке
по выборке 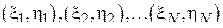 является выборочный коэффициент корреляции, определяемый следующим выражением:
является выборочный коэффициент корреляции, определяемый следующим выражением:
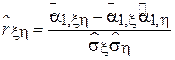 .
.
Здесь:
- 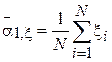 - выборочное математическое ожидание случайной величины
- выборочное математическое ожидание случайной величины 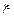 ;
;
- 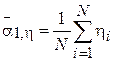 - выборочное математическое ожидание случайной величины
- выборочное математическое ожидание случайной величины 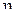 ;
;
- 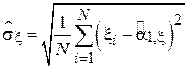 - выборочное СКО случайной величины
- выборочное СКО случайной величины 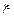 ;
;
- 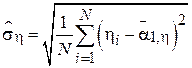 - выборочное СКО случайной величины
- выборочное СКО случайной величины 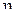 ;
;
- 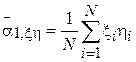 - выборочный первый смешанный момент случайных величин
- выборочный первый смешанный момент случайных величин 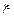 и
и 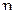 .
.
Дадим выборочному коэффициенту корреляции следующую наглядную интерпретацию. Построим график, на который нанесем точки, соответствующие всем парам 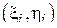 (так называемая диаграмма рассеяния или облако) и проведем через облако прямую линию вида
(так называемая диаграмма рассеяния или облако) и проведем через облако прямую линию вида 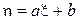 . Коэффициенты этой прямой a и b подберем так, чтобы эта прямая проходила через облако с минимальной невязкой относительной точек
. Коэффициенты этой прямой a и b подберем так, чтобы эта прямая проходила через облако с минимальной невязкой относительной точек 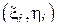 :
:
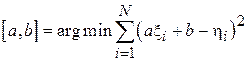 .
.
Такая прямая называется линейной регрессией для выборочных данных 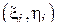 . Тогда выборочный коэффициент корреляции будет прямо пропорционален полученному коэффициенту наклона этой прямой a:
. Тогда выборочный коэффициент корреляции будет прямо пропорционален полученному коэффициенту наклона этой прямой a:
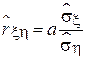 .
.
Примеры диаграмм рассеяния с проведенными прямыми см. на рис. 5.1а – 5.1г.
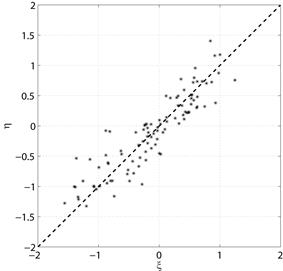 а) Положительная корреляция
а) Положительная корреляция
| 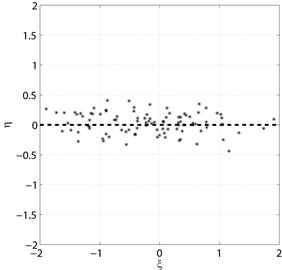 б) Нулевая корреляция
б) Нулевая корреляция
|
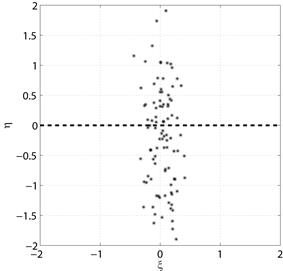 в) Нулевая корреляция
в) Нулевая корреляция
| 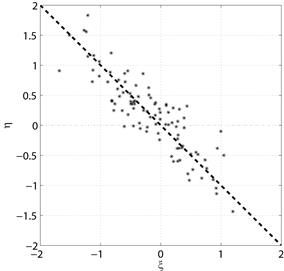 г) Отрицательная корреляция
г) Отрицательная корреляция
|
Рис. 5.1. Диаграммы рассеяния
Анализ временных рядов
Описанный в подразделе 5.3 подход может быть использован также при анализе временных рядов. По определению, временным рядом называется совокупность зафиксированных в определенные моменты времени (как правило, отстоящие на равные интервалы 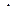 ) значений исследуемого процесса. В этом случае выборка состоит из элементов вида
) значений исследуемого процесса. В этом случае выборка состоит из элементов вида 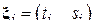 , где
, где 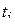 - момент фиксирования i-го отсчета процесса (
- момент фиксирования i-го отсчета процесса ( 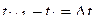 ),
), 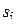 - его значение (см. Примеры 16 и 17). В общем случае si могут являться зависимыми случайными величинами.
- его значение (см. Примеры 16 и 17). В общем случае si могут являться зависимыми случайными величинами.
Через облако, образованное множеством точек 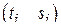 , может быть проведена регрессионная кривая, именуемая также кривой тренда. В случае, если был использован полином первого порядка, говорят, что был вычислен линейный тренд случайного процесса. Тренд позволяет выявить общие, крупномасштабные тенденции в анализируемом процессе.
, может быть проведена регрессионная кривая, именуемая также кривой тренда. В случае, если был использован полином первого порядка, говорят, что был вычислен линейный тренд случайного процесса. Тренд позволяет выявить общие, крупномасштабные тенденции в анализируемом процессе.
Пример 20[7].
Построим график колебания отношения курса евро к курсу доллара за последние 16 лет и аппроксимируем его регрессией 5-го порядка (см. рис. 5.3) [10].
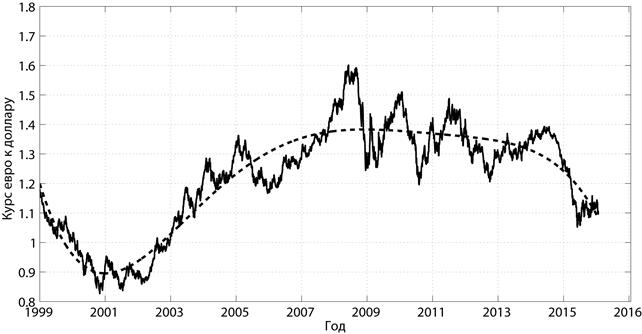
Рис. 5.3. График колебания курса евро к доллару и тренд 5-го порядка
Полином, описывающий тренд, был получен в результате применения выражения (5.4) и имеет следующий вид (здесь x – номер дня, начиная с 01.01.1999):
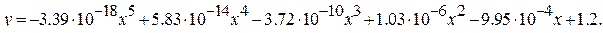
Можно видеть, что тренд отражает основные вехи в мировой экономике за последние годы: спад европейской экономики, связанный с кризисом 2002 года, кризис 2008 года, приведший к ослаблению курса доллара, напряженная политическая ситуация в Европе в 2014-2015 гг.
В случае, если временной ряд демонстрирует неизменное поведение на длительном интервале времени[8], полезным инструментом для его анализа является выборочная корреляционная функция (ВКФ):
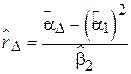 .
.
Здесь 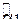 и
и 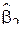 - стандартные оценки математического ожидания и дисперсии по выборке
- стандартные оценки математического ожидания и дисперсии по выборке 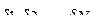 ,
, 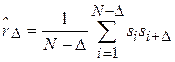 . ВКФ показывает, на сколько быстро убывает коэффициент корреляции между значениями случайного процесса в моменты
. ВКФ показывает, на сколько быстро убывает коэффициент корреляции между значениями случайного процесса в моменты 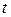 и
и 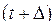 с ростом
с ростом 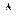 . Иными словами, по характеру ВКФ можно определить, на сколько события, произошедшие с объектом исследования в один момент, связаны с его поведении через момент времени
. Иными словами, по характеру ВКФ можно определить, на сколько события, произошедшие с объектом исследования в один момент, связаны с его поведении через момент времени 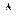 .
.
Пример 21.
Вычтем из графика колебания отношения курса евро к курсу доллара аппроксимирующую его регрессию 5-го порядка (см. Пример 20). Получившийся график приведен на рис. 5.5.
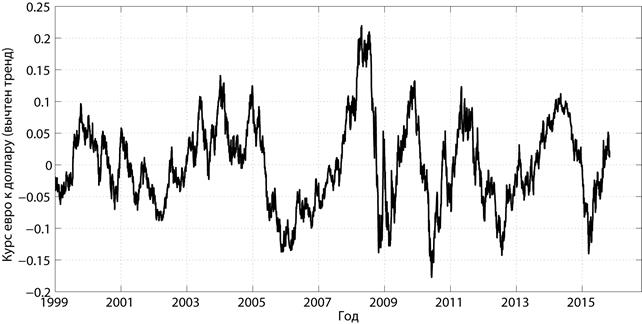
Рис. 5.5. График колебаний курса евро к доллару относительно тренда
Если тренд отражал глобальные мировые события, то данный график характеризует в основном локальные события (на уровне отдельных государств и отраслей промышленности). Видно, что характер полученного случайного процесса остается практически неизменным на протяжении последних 16 лет. Построим его ВКФ (см. рис. 5.6).
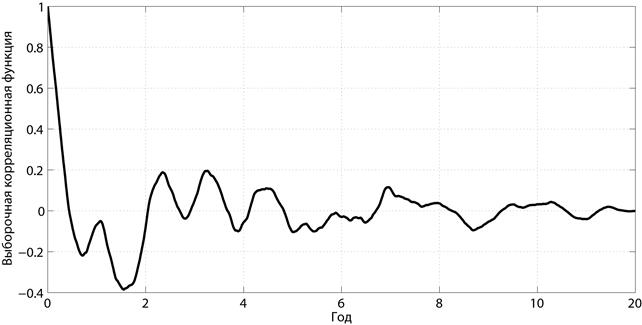
Рис. 5.6. ВКФ локальных колебаний курса евро к доллару
Из полученной зависимости следует, что при 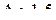 года коэффициент корреляции равен приблизительно -0.4, что говорит о том, что за локальным подъемом курса одной из валют приблизительно через 1.5 года с высокой вероятностью последует его локальный спад. Также можно видеть, что
года коэффициент корреляции равен приблизительно -0.4, что говорит о том, что за локальным подъемом курса одной из валют приблизительно через 1.5 года с высокой вероятностью последует его локальный спад. Также можно видеть, что  лет коэффициент корреляции не превышает 0.1. Из этого можно сделать тот вывод, что при прогнозировании динамики курсов указанных валют достаточно ограничить анализом лишь последних 4 лет.
лет коэффициент корреляции не превышает 0.1. Из этого можно сделать тот вывод, что при прогнозировании динамики курсов указанных валют достаточно ограничить анализом лишь последних 4 лет.
Вопросы для самопроверки
1. Используя МНК вывести формулы для расчета коэффициентов линейной регрессии через значения элементов выборки в явном виде.
2. Вывести формулу для расчёта коэффициентов полиномиальной регрессии (5.4).
3. Объяснить принцип метода наименьших квадратов.
4. Пояснить, почему диаграмма рассеяния, приведенная на рис. 5.1в соответствует нулевой корреляции между случайными величинами.
5. Дана совместная плотность вероятности для пары случайных величин 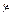 и
и 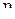 :
: 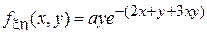 , где
, где 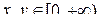 . Выбрать коэффициент a исходя из условий нормировки плотности вероятности. Найти коэффициент корреляции между
. Выбрать коэффициент a исходя из условий нормировки плотности вероятности. Найти коэффициент корреляции между 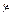 и
и 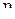 .
.
6. Дана совместная плотность вероятности для пары случайных величин 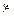 и
и 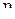 :
: 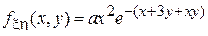 , где
, где 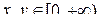 . Выбрать коэффициент a исходя из условий нормировки плотности вероятности. Найти коэффициент корреляции между
. Выбрать коэффициент a исходя из условий нормировки плотности вероятности. Найти коэффициент корреляции между 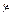 и
и 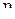 .
.
7. Дана совместная плотность вероятности для пары случайных величин 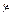 и
и 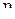 :
: 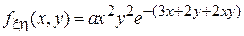 , где
, где 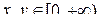 . Выбрать коэффициент a исходя из условий нормировки плотности вероятности. Найти коэффициент корреляции между
. Выбрать коэффициент a исходя из условий нормировки плотности вероятности. Найти коэффициент корреляции между 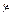 и
и 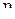 .
.
8. Дана совместная плотность вероятности для пары случайных величин 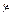 и
и 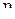 :
: 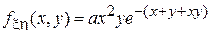 , где
, где 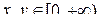 . Выбрать коэффициент a исходя из условий нормировки плотности вероятности. Найти коэффициент корреляции между
. Выбрать коэффициент a исходя из условий нормировки плотности вероятности. Найти коэффициент корреляции между 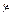 и
и 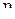 .
.
9. Дана система случайных величин 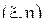 , равномерно распределенных внутри окружности с единичным радиусом. Являются ли эти величины зависимыми? Являются ли они коррелированными? Проверить факт наличия или отсутствия корреляции методом моделирования.
, равномерно распределенных внутри окружности с единичным радиусом. Являются ли эти величины зависимыми? Являются ли они коррелированными? Проверить факт наличия или отсутствия корреляции методом моделирования.
10. Для задачи №17 построить график зависимости дисперсии оценки коэффициента корреляции от объема выборки.
11. Привести пример системы из двух дискретных случайных величин, коэффициент корреляции между которыми равен 0, но случайные величины являются зависимыми.
12. Привести пример системы из двух непрерывных случайных величин, коэффициент корреляции между которыми равен 0, но случайные величины являются зависимыми.
13. Построить график колебаний уровня безработицы по данным, загруженным из источника [10] (код «UNRATE»). Подобрать порядок и коэффициенты полиномиальной регрессии по МНК.
14. Построить график колебаний коэффициента эффективности бюджетных вложений безработицы по данным, загруженным из источника [10] (код «FEDFUNDS»). Подобрать порядок и коэффициенты полиномиальной регрессии по МНК.
15. Построить график роста валового внутреннего продукта (ВВП) по данным, загруженным из источника [10] (код «GDP»). Подобрать порядок и коэффициенты полиномиальной регрессии по МНК.
16. Построить график зависимости государственного долга США как процент от ВВП по данным, загруженным из источника [10] (код «GFDEGDQ188S»). Подобрать порядок и коэффициенты полиномиальной регрессии по МНК.
17. Дано: 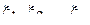 – последовательность независимых, одинаково распределенных случайных величин,
– последовательность независимых, одинаково распределенных случайных величин, 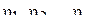 – случайные величины, рассчитанные по формуле
– случайные величины, рассчитанные по формуле 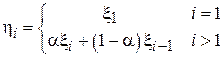 . Найти корреляционную функцию процесса
. Найти корреляционную функцию процесса 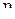 теоретически. Выполнить проверку методом моделирования.
теоретически. Выполнить проверку методом моделирования.
18. Дано: 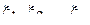 – последовательность независимых, одинаково распределенных случайных величин,
– последовательность независимых, одинаково распределенных случайных величин, 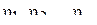 – случайные величины, рассчитанные по формуле
– случайные величины, рассчитанные по формуле 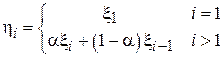 . Найти корреляционную функцию процесса
. Найти корреляционную функцию процесса 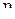 теоретически. Определить, как зависит ширина корреляционной функции от параметра
теоретически. Определить, как зависит ширина корреляционной функции от параметра 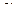 .
.
19. Дано: 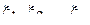 – последовательность независимых, одинаково распределенных случайных величин с
– последовательность независимых, одинаково распределенных случайных величин с 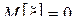 ,
, 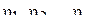 – случайные величины, рассчитанные по формуле:
– случайные величины, рассчитанные по формуле: 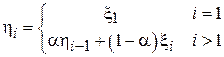 . Найти корреляционную функцию данного процесса и определить, как зависит ширина корреляционной функции от параметра
. Найти корреляционную функцию данного процесса и определить, как зависит ширина корреляционной функции от параметра 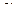 .
.
20. Подбрасываются два игральных кубика, на первом выпадает значение 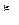 , на втором –
, на втором – 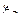 . Вводим случайные величины
. Вводим случайные величины 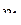 и
и 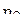 такие, что
такие, что 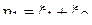 и
и 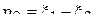 . Найти коэффициент корреляции между величинами
. Найти коэффициент корреляции между величинами 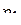 и
и 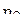 .
.
6. Библиографический список
1. Елисеева И.И., Юзбашев М.М. Общая теория статистики: Учебник / Под ред. И.И. Елисеевой. — 5-е изд., перераб. и доп. — М.: Финансы и статистика, 2004.
2. Фарафонов В. Г., Устимов В. И. Теория вероятностей и математическая статистика: учебное пособие. Ч. 1, Ч. 2. СПб. : Изд-во ГУАП, 2009.
3. Крамер Г. Математические методы статистики. М.: Мир. 1975 г.
4. Вентцель Е. С. Теория вероятности. М.: Наука. 1969 г.
5. Лагутин М.Б. Наглядная математическая статистика. М.: Бином. 2009 г.
6. T. S. Ferguson. An Inconsistent Maximum Likelihood Estimate. Journal of the American Statistical Association, Vol. 77, No. 380. 1982.
7. Чернова Н.И. Математическая статистика. Новосибирск: Изд-во СибГУТИ, 2009.
8. A. C. Cullen, H. C. Frey. Probabilistic Techniques in Exposure Assessment. A Handbook for Dealing with Variability and Uncertainty in Models and Inputs. New-York, Plenum Press, 1999.
9. Мишулина О. А. Статистический анализ и обработка временных рядов. М.: МИФИ, 2004.
10. Информационный ресурс Федерального резервного банка: https://research.stlouisfed.org/fred2/
[1] Авторы хотели бы выразить благодарность студентке группы 4116 Фроловой А.Ю. за помощь в подготовке материала, лежащего в основе данного пособия.
[2] Выборка одинаково распределенных случайных величин называется однородной. При этом элементы однородной выборки могут быть, как зависимы, так и независимы.
[3] При составлении исходной системы уравнений можно использовать как начальные, так и центральные моменты.
[4] При k < 1 основная доля отказов приходится на первое время после начала эксплуатации, k > 1 массовые отказы возникают, начиная с определенного срока эксплуатации
[5] В выражении для дисперсии оценки 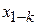 - (1-k) квантиль распределения
- (1-k) квантиль распределения
[6] Зачастую точная верхняя грань эквивалентна максимуму. Таким образом, неформально, теорема Гливенко-Кантелли утверждает, что максимальная ошибка в оценке интегральной функции распределения стремится к нулю с ростом объема выборки.
[7] Данный пример подготовлен студентом гр. 4216 Сафоновым М.В.
[8] Строгое определение стационарных случайных процессов см. в работах [2,4,9].
ЗАДАЧИ И МЕТОДЫ СТАТИСТИЧЕСКОГО ОЦЕНИВАНИЯ
Учебное пособие

Санкт-Петербург
2015
Аннотация
В учебном пособии рассматриваются типовые задачи, возникающие при статистической обработке экспериментальных данных. Основной акцент сделан на задачах выборочного оценивания различных параметров системы случайных величин, отражающих свойства исследуемого объекта. Дается формальное описание наиболее распространенных алгоритмов оценивания таких параметров, например, как моментные и вероятностные характеристики случайной величины, величина сдвига распределения, корреляционные зависимости и т. д. Качество приведенных алгоритмов анализируется при помощи стандартных критериев несмещенности, состоятельности и эффективности. Пособие содержит большое количество примеров использования рассмотренных методов оценивания, а так же индивидуальные задания на закрепление изученного материала.
Оглавление
Введение.. 4
1. Основные определения и понятия математической статистики.. 6
1.1 Предмет математической статистики. 6
1.2 Проведение статистического эксперимента. 7
1.3 Представление случайной величины.. 9
1.4 Свойства оценок. 13
1.4.1 Несмещенность. 13
1.4.2 Состоятельность. 16
1.4.3 Эффективность. 17
1.5 Вопросы для самопроверки. 23
2. Общие методы оценки параметров случайной величины... 25
2.1 Оценка начальных моментов случайной величины.. 25
2.2 Оценка центральных моментов случайной величины.. 27
2.3 Метод моментов. 29
2.4 Метод максимального правдоподобия. 31
2.5 Вопросы для самопроверки. 34
3. Анализ симметричных распределений.. 37
3.1 Квадратичный штраф.. 37
3.2 Симметричные распределения. 38
3.3 Оценки смещения симметричного распределения. 39
3.4 Вопросы для самопроверки. 45
4. Оценка закона распределения случайной величины... 47
4.1 Подходы к оценке закона распределения. 47
4.2 Метод гистограмм.. 47
4.3 Оценка интегральной функции распределения. 51
4.4 Экспресс-оценка закона распределения. 54
4.5 Вопросы для самопроверки. 55
5. Анализ многомерных случайных величин. Построение регрессионных моделей. 57
5.1 Последовательность векторов со случайными и неслучайными компонентами. 57
5.2 Оценка корреляции между компонентами вектора. 58
5.3 Построение полиномиальных регрессий. 62
5.4 Анализ временных рядов. 63
5.5 Вопросы для самопроверки. 67
6. Библиографический список.. 70
Введение
Многие технические, социальные и экономические процессы в мире носят вероятностный характер. Поэтому для широкого круга специалистов важным является приобретение основных знаний в области статистической обработки результатов наблюдений, а также навыков реализации соответствующих алгоритмов на ЭВМ.
Настоящее пособие направлено на закрепление отдельных глав материала, читаемого в курсе «Статистическая обработка информации» для студентов ГУАП. Основной акцент делается на оценивании параметров случайных величин и их систем. Предполагается, что читатель знаком с основами теории вероятности в объеме программы технического ВУЗа.
После освоения очередного раздела предлагается провести самостоятельное исследование с применением ЭВМ для получения практических навыков реализации и анализа рассмотренных алгоритмов. Программы исследований приведены в методических указаниях по выполнению лабораторных работ, выходящих одновременно с настоящим учебным пособием. Не смотря на то, что данные задания не привязаны к конкретной среде программирования, можно порекомендовать применение таких сред компьютерной математики как Octave, Sci-Lab и Matlab.
В пособии принята следующая система обозначений: та информация, на которой авторы хотели бы акцентировать внимание читателя, выделена жирным шрифтом, новые вводимые определения и понятия – курсивом. Случайные величины обозначаются греческими буквами без подстрочных индексов, конкретная реализация случайной величины – соответствующей греческой буквой с индексом, указывающим на номер элемента в выборке. Оценки обозначаются надсимвольным значком ^ (циркумфлекс)[1].
Для более глубокого изучения изложенного материала можно рекомендовать следующую литературу (см. библиографический список в конце пособия):
1. Основные определения и понятия математической статистики
1.1. Предмет математической статистики [1,2]
1.2. Проведение статистического эксперимента [3]
1.3. Представление случайной величины [2, 4]
1.4. Свойства оценок [5]
2. Общие методы оценки параметров случайной величины
2.1. Оценка начальных моментов случайной величины [4]
2.2. Оценка центральных моментов случайной величины [4]
2.3. Метод моментов [3,5]
2.4. Метод максимального правдоподобия [3,5,6]
3. Анализ симметричных распределений [5]
4. Оценка закона распределения случайной величины
4.1. Подходы к оценке закона распределения [2,3,4]
4.2. Метод гистограмм [4, 7]
4.3. Оценка интегральной функции распределения [4, 7]
4.4. Экспресс-оценка закона распределения [8]
5. Анализ многомерных случайных величин. Построение регрессионных моделей.
5.1. Последовательность векторов со случайными и неслучайными компонентами [3, 5]
5.2. Оценка корреляции между компонентами вектора [3, 4, 5]
5.3. Построение полиномиальных регрессий [9]
5.4. Анализ временных рядов [9]
1. Основные определения и понятия математической статистики
Дата: 2019-07-24, просмотров: 418.