По аналогии с выборочным начальным моментом можно сформулировать понятие выборочного центрального момента.

                                          .                              

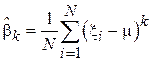Заметим, что для того, чтобы воспользоваться выражением (2.4), необходимо знание истинного значения МО. Приведем свойства выборочного центрального момента. Доказательства этих свойств можно провести по полной аналогии с материалами предыдущего подраздела.

Свойство 1. Оценка 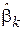 является несмещенной.

Свойство 2. Зависимость дисперсии оценки 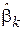 от объема выборки определяется следующим выражением:

                                   .                           

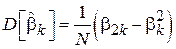Свойство 3. Оценка 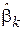 является состоятельной.

Свойство 4. Оценка 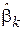 является асимптотически нормальной:

.

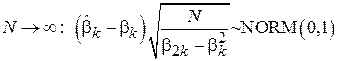Свойство 5. При достаточно большом объеме выборки N, выход 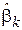 за границы диапазона  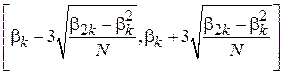является редким событием.

На практике, как правило, прямое использование выражения (2.4) – невозможно, т.к. точное значение 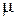 – не известно. Однако величина  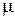может быть оценена заранее, например, при помощи выражения (2.1). Выражение (2.4) при этом принимает вид:

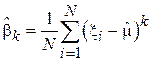
Использование оценки МО вместо истинного значения приводит к тому, что оценка становится смещенной, причем величина смещения принимает весьма сложный вид с ростом k. Так, например:

.

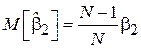Т.е. выборочная оценка дисперсии в случае неизвестного МО является смещенной на величину 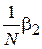. Видно, что величина смещения стремится к нулю с ростом объема выборки. Это же свойство выполняется и для моментов более высоких порядков k. Таким образом, свойство 1 формулируется следующим образом:

Свойство 1. Оценка 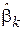 является асимптотически несмещенной.

Свойства 2 – 5 также асимптотически эквиваленты соответствующим свойствам для случая известного МО.

Заметим, что для случая оценки дисперсии, зная величину смещения, несложно найти выражение, дающее несмещенную оценку:

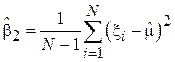
Метод моментов

В тех случаях, когда исследователю необходимо провести оценку произвольных параметров случайной величины (например, границ в равномерном распределении или показателя в экспоненциальном) можно воспользоваться достаточно универсальным методом моментов (ММ). Суть метода заключается в следующем. Параметры случайной величины однозначно задают функцию распределения 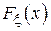, а, значит, и все моменты распределения. Тогда, если необходимо оценить t параметров 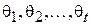, можно составить следующую систему из t уравнений[3]:

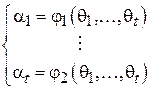
Переразрешив данную систему относительно 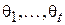, получим новую систему уравнений, позволяющую найти параметры распределения через его моменты:

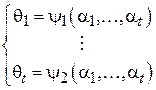
После оценки моментов (например, методами, описанными в подразделах 2.1-2.2) и подстановки их в систему (2.8) получим оценки для искомых параметров распределения.

Пример 11.

Оператор сотовой сети анализирует интервалы времени между звонками, осуществляемыми абонентами. Известно, что эти интервалы распределены по закону, близкому к экспоненциальному. Плотность вероятности для такой случайной величины записывается следующим образом:

                                       .

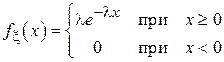Тогда искомым будет параметр 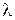. Подставив выражение для плотности вероятности в формулу (1.5) при k = 1 получим систему (2.8):

.

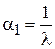Тривиальное переразрешение дает следующую систему (2.9):

.

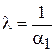Подставив в данное выражение формулу (2.1) для оценки первого начального момента получим следующую оценку параметра :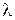

.

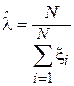Здесь 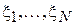 - интервалы времени между звонками, наблюдаемые в процессе работы сети.

Пример 12.

По выборке равномерно распределенных случайных величин необходимо одновременно оценить оба параметра данного распределения (левую границу a и правую границу b). Известно, что:

.

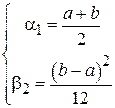Решив данную систему относительно a и b получим:

.

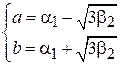Оценив по выборке 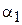 и  и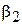, подставив их в данную систему, получим оценки по ММ для a и b.

Очевидным недостатком данного метода является сложность переразрешения системы (2.8) в систему (2.9) для некоторых распределений, а также невысокая точность в случае одновременного оценивания большого количества параметров.