Другим распространенным методом оценивания является метод максимального правдоподобия (ММП). Во многих полезных с точки зрения практики случаях данный метод обладает высокой эффективностью, хотя известен ряд примеров, когда оценка по ММП является несостоятельной.
Пусть задана функция плотности вероятности 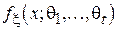 случайной величины
случайной величины 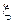 , определяемая набором параметров
, определяемая набором параметров 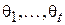 . Тогда оценкой по ММП будет являться такой набор
. Тогда оценкой по ММП будет являться такой набор 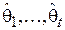 , что:
, что:
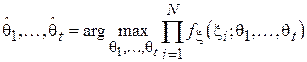 ,
,
где 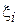 - i-й элемент выборки. В силу монотонности функции логарифма и неотрицательности функции
- i-й элемент выборки. В силу монотонности функции логарифма и неотрицательности функции 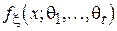 при любом наборе аргументов, можно предложить эквивалентное определение для оценки по МПП:
при любом наборе аргументов, можно предложить эквивалентное определение для оценки по МПП:
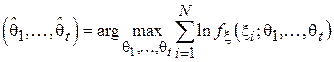 .
.
Пример 13.
Известно, что ошибка определения координаты посредством GPS имеет распределение, близкое к распределению Лапласа, плотность которого описывается следующим выражением:
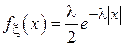 .
.
Из анализа выражения видно, что точность GPS приемника будет определяться параметром распределения 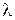 (чем
(чем 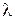 больше, тем точнее работа приемника). Для оценки этого параметра GPS устанавливают в точке, координата которой известна точно и N раз измеряют эту координату, регистрируя каждый раз величину ошибки
больше, тем точнее работа приемника). Для оценки этого параметра GPS устанавливают в точке, координата которой известна точно и N раз измеряют эту координату, регистрируя каждый раз величину ошибки 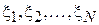 . Оценим по этой выборке параметр
. Оценим по этой выборке параметр 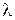 с помощью ММП в форме (2.11).
с помощью ММП в форме (2.11).
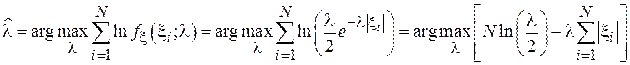
Взяв от выражения правдоподобия производную и приравняв ее к нулю получим:
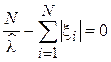 .
.
Тогда оценка по ММП примет следующий вид:
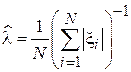 .
.
Пример 14.
В теории надежности широко используется модель, согласно которой время наработки технического устройства до отказа (т.е. время, проходящее с момента начал эксплуатации устройства до момента его поломки) описывается случайной величиной, имеющей распределение Вейбулла:
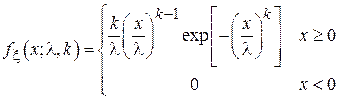
Это распределение – двухпараметрическое с параметрами k (коэффициент формы) и 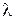 (коэффициент масштаба). Условно можно сказать, что значение параметра k говорит в основном о характере отказов устройства[4], параметр
(коэффициент масштаба). Условно можно сказать, что значение параметра k говорит в основном о характере отказов устройства[4], параметр 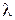 - о среднем сроке эксплуатации. Для оценки значений данных параметров для нового типа устройства изготавливают опытную партию, для каждого элемента которой регистрируют время наработки до отказа
- о среднем сроке эксплуатации. Для оценки значений данных параметров для нового типа устройства изготавливают опытную партию, для каждого элемента которой регистрируют время наработки до отказа 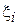 (
( 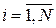 ). Найдем параметры данного распределения по ММП:
). Найдем параметры данного распределения по ММП:
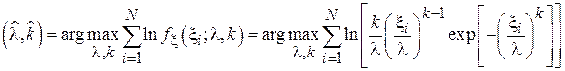
Разложив логарифм произведения в сумму получим:
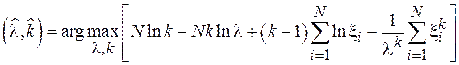
Найдем градиент функции правдоподобия и приравняем его к нулю:
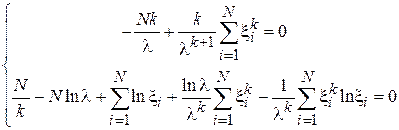 .
.
Из первого уравнения получим:
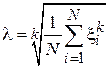 .
.
Подставив данное выражение во второе уравнение и заметив, что 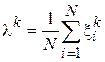 , получим систему в следующем виде:
, получим систему в следующем виде:
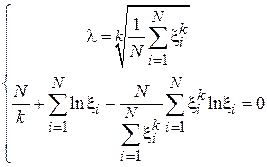 .
.
Перегруппировав слагаемые получим:
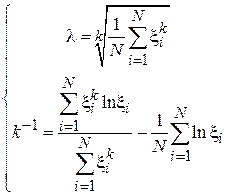 .
.
Численно решив второе уравнение и подставив полученную оценку параметра k в первое уравнение, получим пару оценок 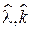 по ММП.
по ММП.
Очевидным недостатком метода максимального правдоподобия является необходимость отыскания максимума от достаточно сложной функции (как, например, в примере 14), что зачастую приходится делать численно.
Вопросы для самопроверки
1. В чем суть центральной предельной теоремы и как она находит свое отражение при нахождении выборочных моментов?
2. Докажите, что оценка дисперсии, приведенная в выражении (2.6), является несмещенной.
3. Как зависит средний квадрат ошибки оценивания момента случайно величины от объема выборки? Почему?
4. В чем состоит закон «трёх сигма»? Продемонстрируйте его на графиках плотности вероятности и интегральной функции распределения.
5. Разработайте моделирующую программу для нахождения вероятности того, что ошибка оценивания превысит заданную величину. Проведите серию вычислительных экспериментов и сопоставьте результаты моделирования с неравенствами Чебышева.
6. Почему график зависимости дисперсии оценки, выполненной по формулам (2.1) и (2.4), от объема выборки, построенный в логарифмическом масштабе, представляет собой прямую линию?
7. Как связаны биномиальное распределение с распределением Бернулли?
8. Доказать, что оценка начального момента (2.1) является несмещенной.
9. Вывести формулу зависимости дисперсии оценки 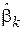 от объема выборки.
от объема выборки.
10. Доказать, что оценка 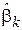 , определяемая выражением (2.4), является состоятельной.
, определяемая выражением (2.4), является состоятельной.
11. Доказать, что оценка 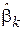 , определяемая выражением (2.4), является асимптотически нормальной.
, определяемая выражением (2.4), является асимптотически нормальной.
12. Методом моделирования проведите исследование эффективности оценки параметра 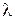 экспоненциального распределения по методу моментов (см. Пример 11).
экспоненциального распределения по методу моментов (см. Пример 11).
13. Методом моделирования проведите исследование эффективности оценки параметров a и b равномерного распределения по методу моментов (см. Пример 12).
14. Выведите выражение для оценки параметра 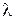 распределения Лапласа по методу моментов (см. Пример 13).
распределения Лапласа по методу моментов (см. Пример 13).
15. Сформулируйте и реализуйте вычислительную процедуру для нахождения параметров k и 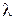 распределения Вейбулла по методу моментов.
распределения Вейбулла по методу моментов.
16. Вывести выражение для оценки математического ожидания гауссовской случайной величины по методу максимального правдоподобия.
17. Вывести выражение для оценки дисперсии гауссовской случайной величины по методу максимального правдоподобия.
18. Вывести выражение для оценки параметра p биномиального распределения по методу максимального правдоподобия.
19. Вывести выражение для оценки параметра N биномиального распределения по методу максимального правдоподобия.
20. Вывести выражение для оценки параметров a и b равномерного распределения по методу максимального правдоподобия.
3. Анализ симметричных распределений
Квадратичный штраф
Как говорилось ранее, для количественного измерения эффективности оценки необходимо выбрать функцию штрафа 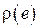 , т.е. меру негативного эффекта, возникающего при той или иной ошибке оценивания
, т.е. меру негативного эффекта, возникающего при той или иной ошибке оценивания 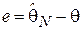 (здесь
(здесь 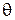 - истинное значение оцениваемого параметра распределения,
- истинное значение оцениваемого параметра распределения, 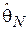 - оценка параметра по выборке объема N).
- оценка параметра по выборке объема N).
Наиболее распространенной функцией является квадратичный штраф, т.е.:
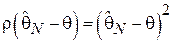
При этом функция риска (т.е. средний штраф, характеризующий точность оценки) записывается следующим образом:
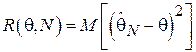 .
.
Чем меньше значение функции риска, тем более эффективной является оценка. Как видно из выражения (3.2), если оценка 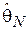 является несмещенной и
является несмещенной и 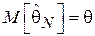 , то функция риска совпадает с дисперсией оценки:
, то функция риска совпадает с дисперсией оценки:
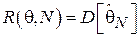 .
.
Так, например, для оценки математического ожидания методом выборочного среднего (см. подразделы 2.2 и 2.3):
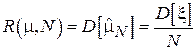 .
.
Симметричные распределения
В данном разделе сравнение эффективности оценок будет иллюстрироваться при помощи симметричных распределений. Будем называть распределение случайной величины 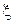 симметричным, если для него существует такое c, что для
симметричным, если для него существует такое c, что для 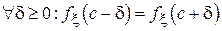 . Очевидно, что при этом число c будет являться центром симметрии плотности вероятности или смещением распределения относительно начала координат. Как правило, смещение соответствует медиане симметричного распределения (в случае, если медиана может быть однозначно определена) и/или математическому ожиданию (в случае существования первого начального момента). На рис. 3.1 приведены примеры симметричных распределений: равномерного, нормального, биномиального и распределения Лапласа.
. Очевидно, что при этом число c будет являться центром симметрии плотности вероятности или смещением распределения относительно начала координат. Как правило, смещение соответствует медиане симметричного распределения (в случае, если медиана может быть однозначно определена) и/или математическому ожиданию (в случае существования первого начального момента). На рис. 3.1 приведены примеры симметричных распределений: равномерного, нормального, биномиального и распределения Лапласа.
Существует ряд задач, для решения которых необходимо оценивание смещения симметричного распределения. Примером может служить сравнение качества деталей, изготовленных по двум различным методикам. Сравнение можно производить путем оценки погрешности изготовления, т.е. анализа случайных величин 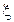 и
и 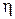 , характеризующих погрешность изготовления детали по 1-й и 2-й методике соответственно.
, характеризующих погрешность изготовления детали по 1-й и 2-й методике соответственно.
Для определения погрешности рассмотрим процесс изготовления детали по двум разным методикам. Пусть: 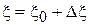 , где
, где 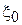 - постоянная величина погрешности, обусловленная методикой изготовления,
- постоянная величина погрешности, обусловленная методикой изготовления, 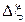 - случайная величина погрешности, обусловленная не зависящими от методики факторами. Аналогично
- случайная величина погрешности, обусловленная не зависящими от методики факторами. Аналогично 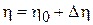 . Будем считать, что
. Будем считать, что 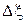 и
и 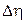 являются независимыми одинаково распределенными случайными величинами с плотностью вероятности
являются независимыми одинаково распределенными случайными величинами с плотностью вероятности 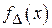 . Введем величину
. Введем величину 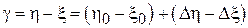 . Известно, что, если две случайные величины (в данном случае
. Известно, что, если две случайные величины (в данном случае 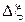 и
и 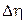 ) – независимы и одинаково распределены, то их разница имеет симметричное распределение с нулевым смещением, определяемое следующим выражением:
) – независимы и одинаково распределены, то их разница имеет симметричное распределение с нулевым смещением, определяемое следующим выражением:
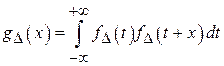
Таким образом, случайная величина 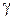 будет характеризоваться симметричной плотностью вероятности
будет характеризоваться симметричной плотностью вероятности 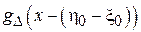 со смещением
со смещением 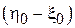 относительно нуля. Если смещение имеет положительный знак (
относительно нуля. Если смещение имеет положительный знак ( 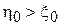 ), то первая методика позволяет выпускать более качественные детали, чем вторая и наоборот.
), то первая методика позволяет выпускать более качественные детали, чем вторая и наоборот.
Для оценки величины смещения изготавливаются две партии деталей, для которых измеренные величины погрешности записываются через 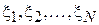 и
и 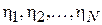 . Тогда можно составить выборку разностей
. Тогда можно составить выборку разностей 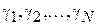 , где
, где 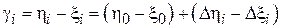 . Далее возникает задача оценки по выборке симметрично распределенных случайных величин
. Далее возникает задача оценки по выборке симметрично распределенных случайных величин 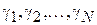 величины их смещения
величины их смещения 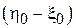 .
.
Дата: 2019-07-24, просмотров: 375.