Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

                           на  основе аксиоматики

Цели урока:

Главная цель: обобщение, систематизация, закрепление полученных знаний и развитие их в перспективе

Общекультурная и научная цели: развитие визуального, наглядно-образного типов мышления, развитие интеллекта: пространственные абстракции, их общность, анализ и синтез геометрических образов .

Воспитательные цели:

аккуратность, коллективизм, ответственность за себя и товарищей, дружбу, взаимопомощь.

Ход урока:

Введение:

Что изучает стереометрия?

Стереометрия знакомит с разнообразием геометрических тел, формирует необходимые пространственные представления.

Стереометрия знакомит с разнообразием геометрических тел, формирует необходимые пространственные представления.

Стереометрия знакомит с разнообразием геометрических тел, формирует необходимые пространственные представления.

"Те, кто влюбляются в практику без теории, уподобляются мореплавателю, садящемуся на корабль без руля и компаса и потому никогда не знающему, куда он плывет".

«Леонардо да Винчи».

Повторение теоретического материала:

1. Аксиомы стереометрии:

Через любые три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна.

Если две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости.

Если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей.

2. Следствия из аксиом стереометрии

1. Через прямую и не лежащую на ней точку проходит плоскость, и притом только одна.

 

2. Через две пересекающиеся прямые проходит плоскость, и притом только одна.

 

Взаимное расположение двух прямых в пространстве

Две прямые лежат в одной плоскости

1. Прямые параллельны (Нет общих точек)

2. Прямые пересекаются (Одна общая точка).

Не лежат в одной плоскости:

3 . Прямые скрещивающиеся

Взаимное расположение прямой и плоскости в пространстве

1. Прямая лежит в плоскости

2. Прямая пересекает плоскость

3. Прямая параллельна плоскости.

Признак параллельности прямой и плоскости:

Если прямая, не лежащая в данной плоскости, параллельна какой-нибудь прямой, лежащей в этой плоскости, то она параллельна данной плоскости.

Способы задания плоскостей

По трем точкам (аксиома 1)

По прямой и не лежащей на ней точке (следствие 1)

По двум пересекающимся прямым (следствие 2)

По двум параллельным прямым (по определению параллельных прямых).

Взаимное расположение плоскости и многогранника

Нет точек пересечения

Одна точка пересечения

Пересечением является отрезок

Пересечением является многоугольник

Разбор задач по теме: Сечение.

Используя полученные знания, применим их к построению сечений многогранников на основе аксиоматики

ПРОБЛЕМА!!! (Что называется сечением плоскостью).

Многоугольник, полученный при пересечении многогранника и плоскости, называется сечением многогранника указанной плоскостью

Какие многоугольники могут получиться в сечении параллелепипеда?

 Какие многоугольники могут получиться в сечении тетраэдра?

Разбор задач на построение сечения многогранника плоскостью на основе знаний аксиоматики.

№1. Построить сечение, определенное точками K , L , M .

N2. Построить сечение, определяемое параллельными прямыми АА₁ и CC₁.

N3. Построить сечение, определяемое пересекающимися прямыми АС₁ и А₁С.

N4. Построить сечение по прямой BC и точке М.

N5. Определите вид сечения куба АВСДА₁В₁С₁Д₁ плоскостью, проходящей через ребро А₁Д₁ и середину ребра ВВ₁.

N6. Постройте сечение куба плоскостью, проходящей через точку М и прямую АС .

N7. Построить сечение правильной призмы плоскостью, проходящей через ребро АВ и точку М середину ребра В₁С₁.

N8. Построить сечение пирамиды плоскостью, проходящей через точку К и параллельно плоскости основания пирамиды.

МЕТОД СЛЕДОВ

Суть метода : построение вспомогательной прямой, являющейся линией пересечения секущей плоскости с плоскостью грани фигуры.

Эту линию называют следом секущей      плоскости.

№1. Дана пирамида MABCD. Постройте сечение пирамиды, проходящее через точки P, Q, R.

№2. Постройте сечение куба, проходящее через точки P, М, К.

Закрепление рассмотренного материала.

Самостоятельная работа (с последующей проверкой).

Если вы хотите научиться плавать, то смело входите в воду,

а если хотите научиться решать задачи, то решайте их

(Д. Пойа).

Работа учащихся: разбор задач с последующим их выполнением в группе

№1. Постройте сечение треугольной пирамиды ABCD, так что бы плоскость сечения была перпендикулярна основанию и делила пополам стороны основания треугольной пирамиды.

№2. Построить сечение четырехугольной пирамиды QWBCE плоскостью, проходящей через сторону основания CB и точку А на одном из ее боковых ребер QW.

№3.Построить сечение призмы QWERUYTI, так что бы плоскость сечения проходила через прямую a в плоскости нижнего основания призмы и точку A на одном из боковых ребер WT.

№4. Изобразите сечение параллелепипеда ABCDHGSF, проходящее через точки М, К, Р на его ребрах.

№5. Изобразите сечение параллелепипеда, проходящее через точки М, К, Р на его ребрах.

№6.* Построить сечение призмы ABCDFEGHKL плоскостью, проходящей через три произвольные точки X , Y и Z на поверхности (не на ребрах) призмы.

№7. * Сечение пирамиды SABCDE плоскостью, проходящей через точку M ребра AS параллельно грани SCD .

Повторение теоретического материала:

1.определение параллельных плоскостей;

2. признак параллельности двух плоскостей;

3.свойства параллельных плоскостей.

Решение задач по теме: Параллельность плоскостей

№51,52 стр.23 (устно) .

Ершов А.П.С-8 стр.22,с-6 стр.89.

№1. Даны параллельные плоскости α и β. Параллельные прямые пересекают плоскость α в точках А и В, а плоскость β – точках 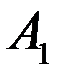и .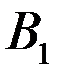

а) Докажите, что ;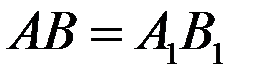

 б) Докажите, что .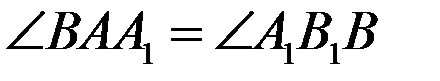

№2. Параллельные прямые a и b пересекают одну из двух параллельных плоскостей в точках 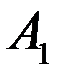и 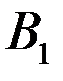, а другую - в точках 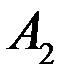и 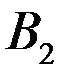соответственно.

Докажите, что .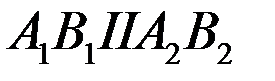

Найдите 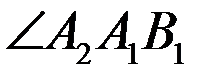, если .

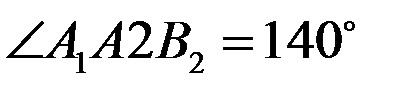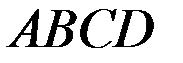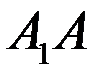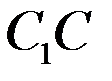№3. Через вершины Аи С параллелограмма проведены параллельные прямые  и , не лежащие в плоскости параллелограмма.

а) Докажите параллельность плоскосте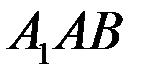й ( )и ( ).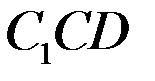

б) Докажите параллельность плоскосте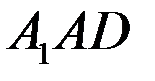й ( )и ( ).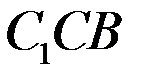

Дома:               повторить п.10-14,задачи №,54,№63(а).

№1. Постройте сечение треугольной пирамиды ABCD, так что бы плоскость сечения была перпендикулярна основанию и делила пополам стороны основания треугольной пирамиды.

№2. Построить сечение четырехугольной пирамиды QWBCE плоскостью, проходящей через сторону основания CB и точку А на одном из ее боковых ребер QW.

№3.Построить сечение призмы QWERUYTI, так что бы плоскость сечения проходила через прямую a в плоскости нижнего основания призмы и точку A на одном из боковых ребер WT.

№4. Изобразите сечение параллелепипеда ABCDHGSF, проходящее через точки М, К, Р на его ребрах.

№5. Изобразите сечение параллелепипеда, проходящее через точки М, К, Р на его ребрах.

№6.* Построить сечение призмы ABCDFEGHKL плоскостью, проходящей через три произвольные точки X , Y и Z на поверхности (не на ребрах) призмы.

№7. * Сечение пирамиды SABCDE плоскостью, проходящей через точку M ребра AS параллельно грани SCD .

Урок физики в 7 классе

Бортикова Галина Ивановна,

учитель физики

высшей квалификационной категории

Условия плавания тел

Цели урока :

На опыте выяснить условия, при которых тело плавает и при каких тонет.

Добиться усвоения учащимися условий плавания тел на основе изученного понятия об архимедовой силе.

Развивать умения учащихся определять архимедову силу с помощью мерного стакана, делать выводы по результатам экспериментальных заданий.

Показать использование условий плавания тел в технике, в народном хозяйстве.

Развивать творческую активность, творческие способности уча­щихся.

Методы обучения: Беседа. Фронтальные опыты. Де­монстрация слайдов. Логиче­ские выводы и интуитивные догадки школьников. Записи на доске и в тетрадях.

Оборудование: Лабораторное: стаканы  с водой, набор тел разной плотности, мензурка, пузырьки с водой, динамометр, клубень картофеля, стакан с раствором соли.

Демонстрационное: сосуд с водой, клубень картофеля, пластмассовая бутылка с водой и пробиркой (картезианский водолаз).

Общее: Компьютер, проектор, презентация, плакаты, фломастеры, раздаточные материалы (приложения 1 и 2),  

Литература: 1. Перышкин А.В., Родина Н.А. Физика 7.- М.: Просвещение 1989.

2. Методика преподования физики в 7 – 8 классах средней школы./ Под ред. А.В. Усовой. - М.: Просвещение, 1990.

Структура занятия:

1. Организационный момент

2. Актуализация знаний (проблемный опыт).

3. Изучение нового материала выяснение условий плавания тел (теоретическое и практическое доказательства). Практическая работа.

4. Физ. минутка.

5. Изучение нового материала (продолжение) проблемный опыт, теоретическое обоснование. Работа с таблицей. Флеш-анимация.

6. Закрепление изученного материала. ТЕСТ.

7. Домашнее задание. Проблемное. Картезианский водолаз.

8. Рефлексия.

Ход урока.

1. Организационный момент. 2 мин

- Здравствуйте ребята, уважаемые члены жюри. Меня зовут Бортикова Галина Ивановна. Урок физики сегодня буду проводить я.

Представьте, что наш кабинет – это лаборатория большого научно- исследовательского институт имени великого ученого Архимеда.

 СЛАЙД АРХИМЕД.

Основная цель института - познание законов природы и использование достижений физики на благо развития цивилизации.

Я - научный руководитель лаборатории «Плавания тел», а вы все мои сотрудники.

Начнём работу в нашем научно-исследовательском институте.

Стук в дверь. Депеша. Срочное сообщение. Дорогие сотрудники, на причале у Амура стоял танкер с нефтью, по непонятной причине произошел взрыв нескольких цистерн, нефть горит, разливается, причины катастрофы выясняются, нас просят помочь как можно быстрее подсказать способ тушения пожара.