При гармоническом воздействии на линейную цепь все токи и напряжения имеют форму гармонических колебаний, поэтому задача расчета цепи сводится к нахождению амплитуд и начальных фаз этих колебаний. В связи с этим был разработан метод комплексных амплитуд, основанный на представлении гармонических функций в виде проекций вращающихся векторов, которые выражаются аналитически в комплексной форме. Метод удобно сочетает аналитические расчеты с геометрическими представлениями.
Гармонические колебания согласно методу комплексных амплитуд могут быть представлены как проекции вектора U m на комплексной плоскости вращающегося против часовой стрелки с угловой частотой ω (рис. 5.1) на оси координат.
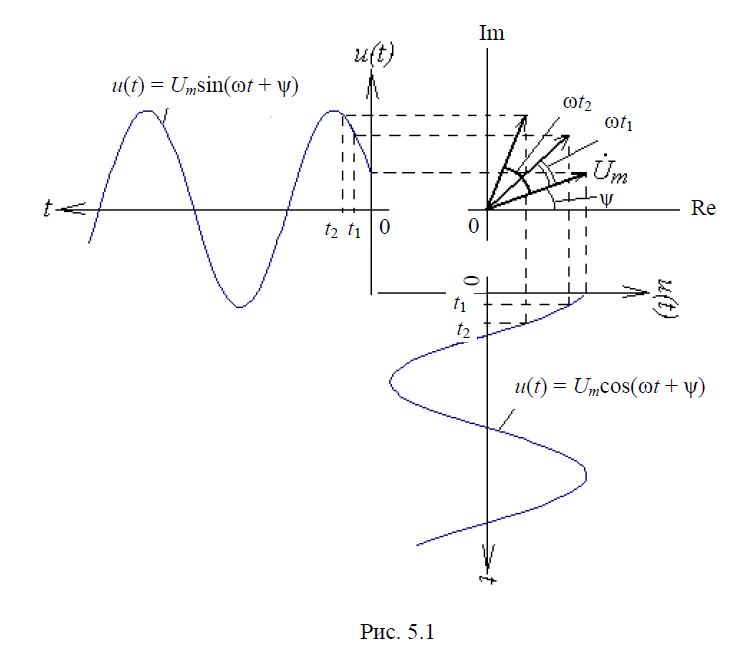
Проекция вектора на вещественную ось представляет собой мгновенное значение, выражаемое косинусоидальной функцией
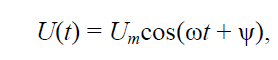
а на мнимую ось – синусоидальной функцией
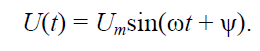
Символический вектор на комплексной плоскости математически может быть представлен в трех формах:
· алгебраической
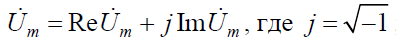
· показательной
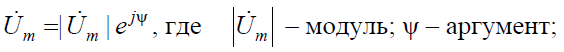
· тригонометрической
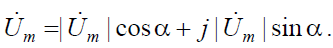
Модуль вектора
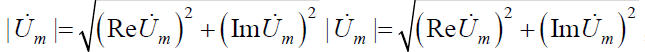
Аргумент
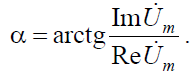
В случае гармонического колебания аргумент комплексного числа U m является функцией времени α = ω · t + ψ.
Поэтому число, символизирующее вращающийся вектор, выражается в показательной форме
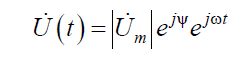
в тригонометрической форме
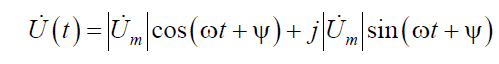
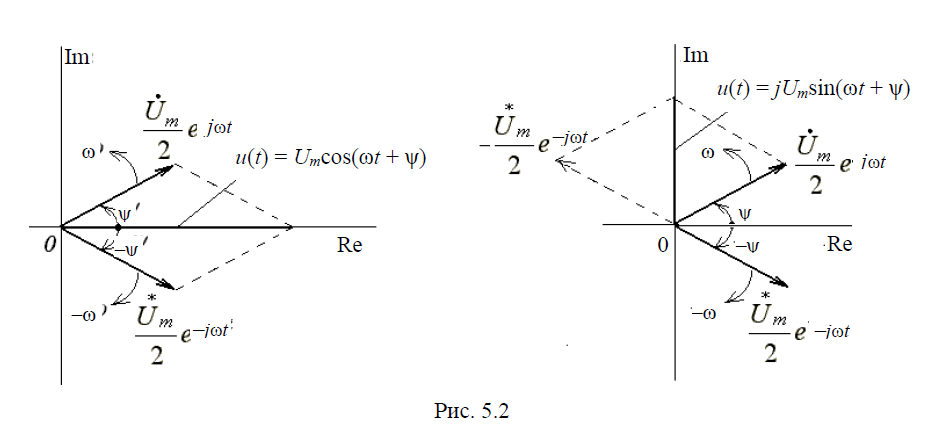
Кроме рассмотренного выше, возможен и несколько иной способ представления гармонических колебаний в виде двух вращающихся навстречу векторов (рис. 5.2).
На основании формулы Эйлера:
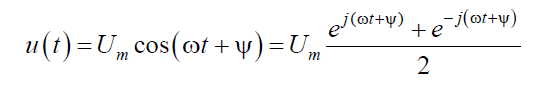
Или
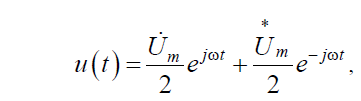
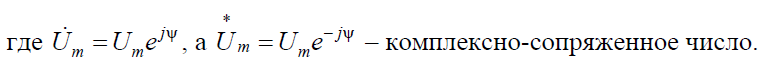
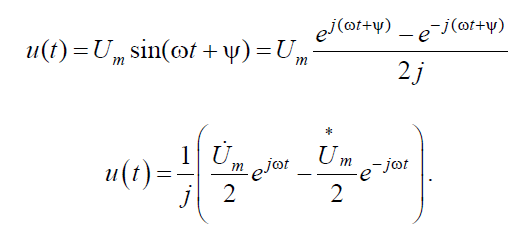
Вращение векторов в отрицательном направлении (по ходу часовой стрелки (рис. 5.2) связано с понятием отрицательной частоты, что, конечно, лишено физического смысла, однако позволяет упростить решение многих задач в радиотехнике и электронике.
Таким образом, при рассмотрении напряжений и токов в цепи при гармоническом воздействии может быть построена векторная диаграмма, представляющая собой совокупность радиус-векторов, отображающих комплексные амплитуды колебаний и вращающихся на комплексной плоскости против часовой стрелки с угловой скоростью ω.
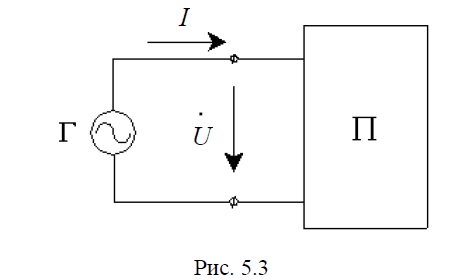
Поскольку взаимное расположение векторов на диаграмме не изменяется, то удобно рассматривать комплексные амплитуды напряжений и токов в момент времени t = 0.
На рис. 5.3 приведено схематическое изображение цепи переменного тока.
Генератор гармонических колебаний питает пассивный двухполюсник, состоящий из сопротивлений, индуктивностей и емкостей. Отношение комплексных амплитуд напряжения U и тока I на входе двухполюсника называется его комплексным входным сопротивлением:
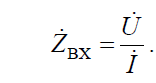
Величина, обратная комплексному сопротивлению, называется его комплексной проводимостью
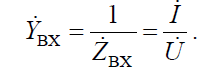
Учитывая, что
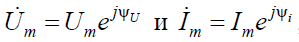
Получаем
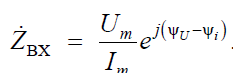
Отношение 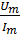 – полное входное сопротивление (модуль); ψU – ψi – сдвиг фаз между напряжением и током.
– полное входное сопротивление (модуль); ψU – ψi – сдвиг фаз между напряжением и током.
Как всякое комплексное число, комплексное сопротивление и комплексная проводимость могут быть представлены в показательной, алгебраической и тригонометрической формах:
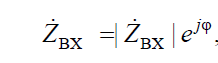
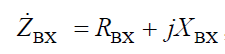
где Rвх – вещественная активная составляющая; Xвх – мнимая реактивная составляющая комплексного сопротивления
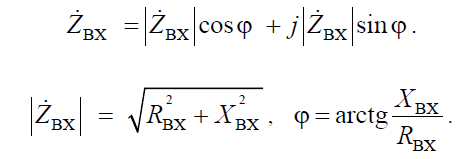
Дата: 2019-07-23, просмотров: 1262.