В общем случае искомые токи и напряжения в ветвях сложной цепи могут быть найдены в результате совместного решения системы уравнений, выражающих первый и второй законы Кирхгофа для заданной электрической цепи.

Пусть в схеме, содержащей p ветвей и q узлов, заданы величины элементов ветвей, ЭДС и токи источников. Необходимо найти токи во всех ветвях цепи.

По первому закону Кирхгофа записываются q – 1 независимых уравнений. Уравнение для q-го узла является следствием предыдущих, в качестве последнего – опорного – узла целесообразно выбрать узел, в котором сходится максимальное число ветвей.

По второму закону Кирхгофа записывается p – q + 1 независимых уравнений для независимых контуров (отличающихся друг от друга хотя бы одной ветвью).

Таким образом, для расчета электрической цепи с помощью законов Кирхгофа необходимо составить столько уравнений, сколько в цепи ветвей.

Решая систему уравнений, находятся искомые токи, а зная сопротивления ветвей, можно найти напряжения между узлами. Если ток в ветви получился со знаком (–), то направление его в действительности противоположно выбранному направлению.

Метод контурных токов

Для сокращения количества уравнений в расчетах токов в цепи часто используется метод контурных токов, являющийся модификацией метода Кирхгофа. При расчете токов этим методом вводят понятие контурного тока как тока в главной ветви независимого контура. Уравнения составляются по второму закону Кирхгофа для независимых контуров, т. е. получается система уравнений с меньшим числом переменных, что является преимуществом метода контурных токов.

Пример:

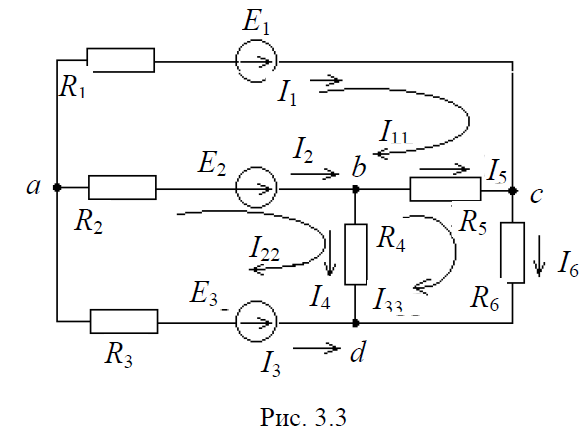
Для схемы (рис. 3.3) имеем:

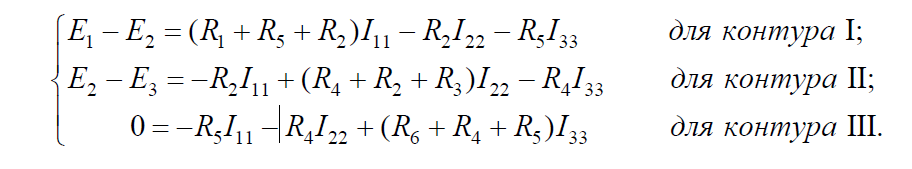
Определив контурные токи из полученной системы уравнений, найдем токи в ветвях:

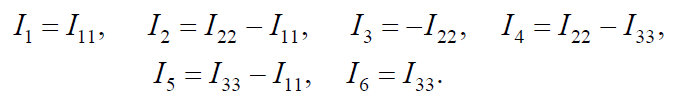
Следует отметить, что при одинаковом направлении контурных токов в системе уравнений суммы сопротивлений, принадлежащих каждому контуру – собственное сопротивление контуров, входят со знаком плюс, а общие сопротивления двух контуров входят со знаком минус.

В общем случае для n-контурной схемы получается n уравнений:

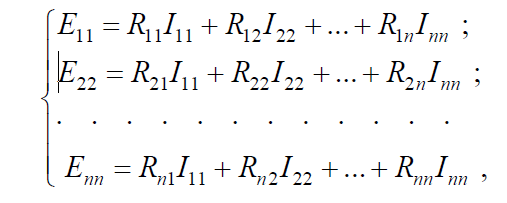
где R11, R22, ..., Rnn – собственное сопротивление контуров;

Rik, ..., Rki – общие сопротивления i-го и k-го контуров.

E11, E22, ..., Enn – контурные ЭДС, алгебраическая сумма ЭДС в каждом контуре.

Решая систему уравнений, находим значения контурных токов. Токи в ветвях находятся как алгебраическая сумма соответствующих контурных токов.

Метод наложения

Ток в любой k-й ветви сложной электрической цепи можно найти, составив уравнения по методу контурных токов, выбрав контуры так, чтобы k-я ветвь входила только в один контур. Тогда ток в k-й ветви будет равен контурному току:

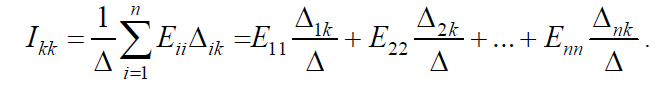
Каждое слагаемое в правой части представляет собой ток, вызванный в k-й ветви соответствующей контурной ЭДС. Например,

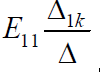 – составляющая тока k-й ветви, вызванная контурной ЭДС E11. Каждая же из контурных ЭДС есть алгебраическая сумма ЭДС ветвей, входящих в соответствующий контур.

Таким образом, ток в k-й ветви, создаваемый несколькими источниками ЭДС, включенными в разных участках схемы, равен алгебраической сумме токов, вызываемых каждой из ЭДС в отдельности. Это и есть принцип суперпозиции или наложения.

Этот принцип нашел применение в методе, получившем название «метод наложения». При расчете токов в ветвях цепи поступают следующим образом: поочередно рассчитывают токи, возникающие от действия каждой ЭДС, мысленно удаляя остальные ЭДС из схемы, но оставляя в схеме внутренние сопротивления источников. Ток в ветвях находят как алгебраическую сумму частичных токов от каждого источника.

Если в цепи заданы источники тока и ЭДС, то ток в любой ветви находится также как сумма токов от действия тех и других источников.

Принцип суперпозиции справедлив только для линейных цепей и называется принципом независимости действия, так как базируется на предположении, что каждое слагаемое сложного воздействия на линейную цепь вызывает свой отклик независимо от того, действуют ли в системе другие слагаемые.

Метод узловых напряжений

Метод узловых напряжений является наиболее общим и широко применяется для расчета электрических цепей, в частности в различных программах автоматизированного проектирования электронных схем.

Ток в любой ветви сложной цепи можно найти, определив разность потенциалов между узлами. Метод расчета, основанный на определении напряжений между узлами сложной цепи, называют методом узловых напряжений (узловых потенциалов).

Число неизвестных в этом методе определяется числом уравнений, которые необходимо составить по первому закону Кирхгофа, т. е. метод узловых напряжений тоже является модификацией метода Кирхгофа. Данный метод имеет преимущества по сравнению с методом контурных токов, когда количество узлов меньше числа независимых контуров сложной цепи. Приняв потенциал одного из узлов (базисного или опорного) равным нулю, получим некоторые напряжения остальных узлов относительно базисного, называемые узловыми напряжениями.

Определим токи во всех ветвях цепи (рис. 3.4), приведенной в примере.

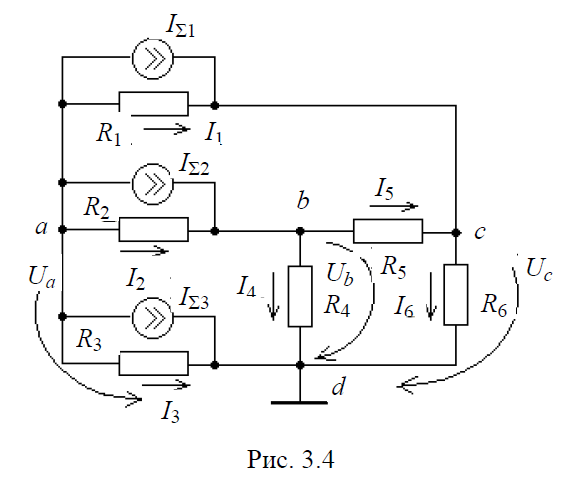
Для узлов a, b, с система уравнений, составленных по первому закону Кирхгофа, следующая

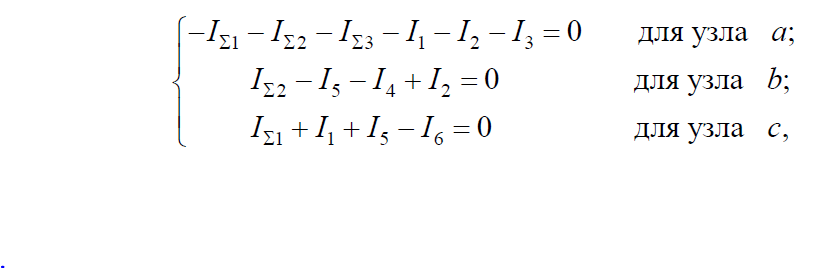
где IΣ1, IΣ2, IΣ3 – токи источников тока.

Токи, протекающие через сопротивления,

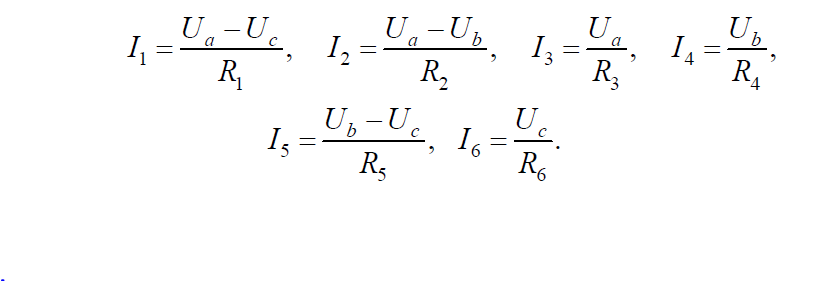
Подставив эти значения в последнюю систему уравнений, получим:

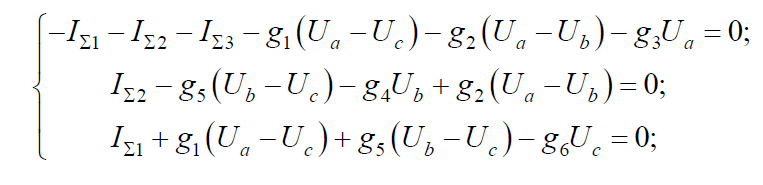
где gk = 1/Rk.

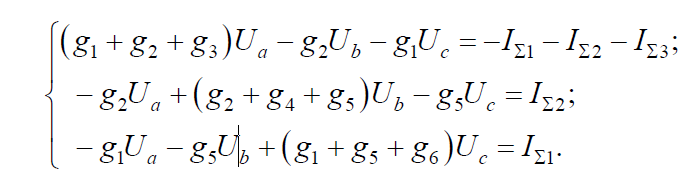
Величины, представляющие собой сумму проводимостей ветвей, сходящихся в данном узле, называются собственной проводимостью узла, величина, равная проводимости ветви между узлами, входящая со знаком минус в систему уравнений, называется общей проводимостью между узлами.

Решив данную систему уравнений, получим узловые напряжения и далее по закону Ома определим токи в ветвях.

В общем случае для сложной цепи, содержащей q узлов:

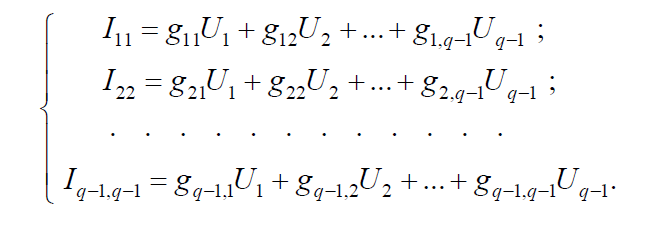
Здесь I11, I22, ..., Iq – 1,q – 1 – алгебраическая сумма токов источников, связанныхс узлами; gii – собственная проводимость i-го узла; gik – общая проводимость между i-м и k-м узлами, входящая со знаком (–) при выбранном направлении узловых напряжений к базисному узлу.

Решив систему уравнений с помощью определителей, получим:

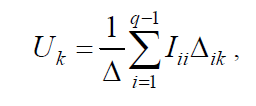
где Δ – определитель системы

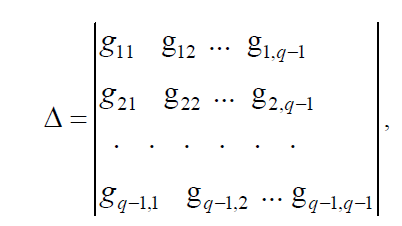
Δik – алгебраическое дополнение элемента gik, полученное из определителя Δ вычеркиванием k-го столбца и i-й строки и умножением полученного определителя на

 (– 1)(1 + k).

В развернутом виде:

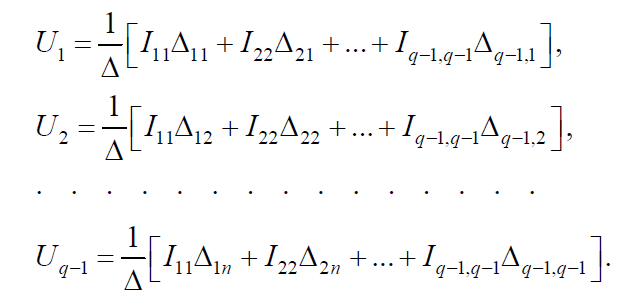
Из последних уравнений следует, что узловые напряжения определяются алгебраической суммой частных узловых напряжений, обусловленных действием каждого источника тока, т. е. как и в методе контурных токов, эти уравнения отражают принцип наложения, характерный для линейных электрических цепей.

Изложенные правила составления узловых уравнений справедливы и для цепей с зависимыми источниками тока, т. е. ИТУН и ИТУТ. В уравнениях появляются дополнительные слагаемые, обусловленные взаимной проводимостью между узлами через зависимые источники.