Параллельным колебательным контуром называется цепь (рис. 9.1), составленная из катушки индуктивности и конденсатора, подключенных параллельно к выходным зажимам источника.

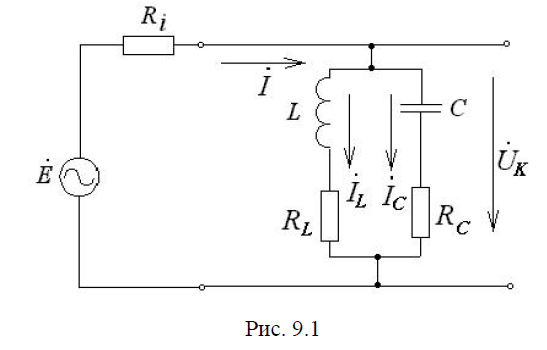
Если на входных зажимах действует источник с Ri = 0, то E =UK и согласно первому закону Кирхгофа I = IL + IC,

где

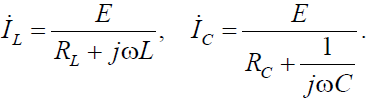
В зависимости от соотношения XL = ωL и X_C =1/ωC можно наблюдать

три режима работы контура.

При X_C> X_L ток в индуктивной ветви

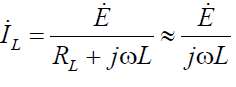
Этот ток отстает от напряжения на контуре на угол

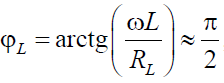
Ток в емкостной ветви

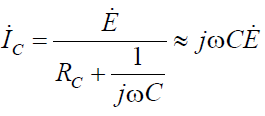
Ток IC опережает напряжение на контуре на угол

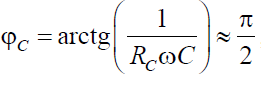
Очевидно, что ток IC > IL. Ток I в неразветвленной части цепи опережает напряжение на контуре на угол φ, т. е. реактивная составляющая входного сопротивления имеет емкостный характер.

Векторная диаграмма токов и напряжения на контуре для этого режима приведена на рис. 9.2, а.

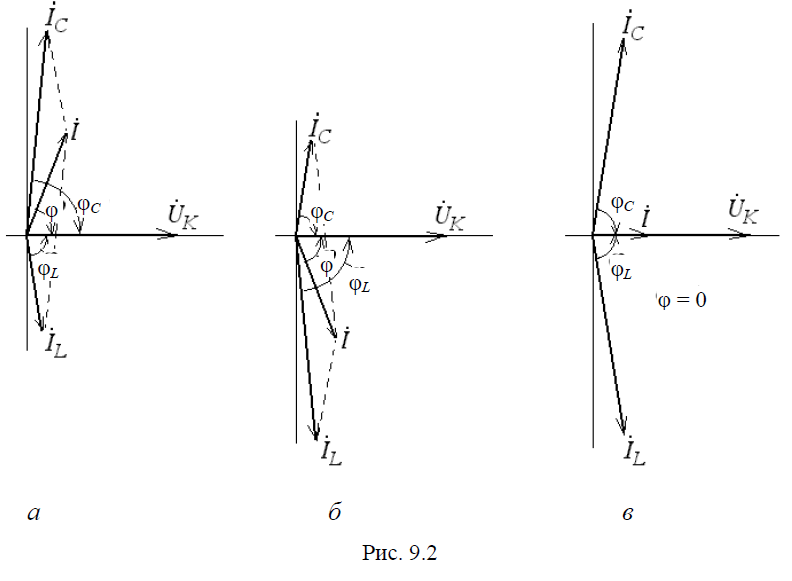
При ω L < 1/ ωC , I_C < I_L. Ток I в неразветвленной части цепи (рис. 9.2, б)отстает от напряжения на контуре на угол φ, т. е. реактивная составляющая входного сопротивления имеет индуктивный характер.

 При ω₀ L = 1/ω₀ C,  I_C ≈ I_L. Ток I в неразветвленной части цепи (рис. 9.2, в) совпадает по фазе с напряжением на контуре, т. е. реактивная составляющая входного сопротивления равна нулю. Режим цепи, при котором реактивная составляющая входной проводимости равна нулю, называется резонансом токов.

Резонансная частота с учетом RL и RC находится из условия равенства нулю реактивной составляющей входной проводимости

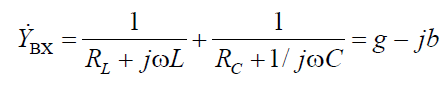
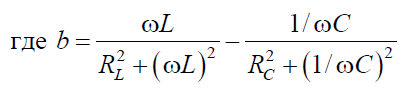
b = 0 при ω₀′ , определяемой из условия

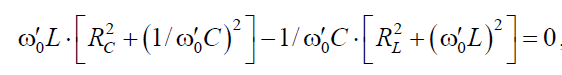
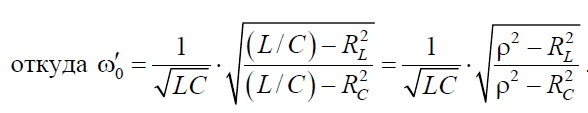
В случае идеального контура (RL = RC = 0) токи I_{L P} = I_CP в ветвях равны по величине и противоположны по фазе, следовательно, ток в неразветвленной цепи равен нулю. Контур не потребляет энергию от генератора и происходит периодическое колебание энергии между электрическим и магнитным полями конденсатора и индуктивности за счет первоначально внесенной энергии при подключении генератора.

Частотные характеристики параллельного контура

Комплексное входное сопротивление контура

при RL <<ωL  и RC << 1/ωC

,

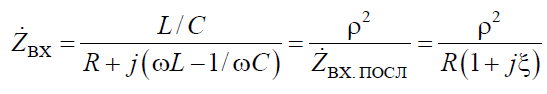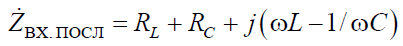 - входное сопротивление последовательного контура, составленного из тех же элементов

 Разделив вещественную и мнимую часть комплексного входного сопротивления, получим:

Модуль входного сопротивления

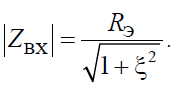
Амплитудно-частотная характеристика

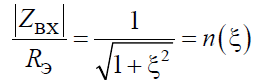
АЧХимеет

такой же вид, как и резонансная кривая последовательного контура; ФЧХ представляет собой зеркальное отображение ФЧХ последовательного контура.

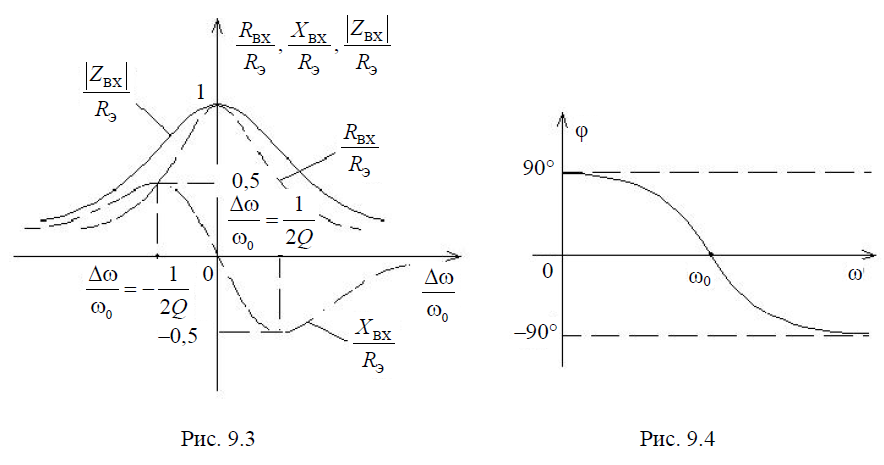
X_BX имеет максимум при

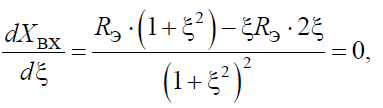
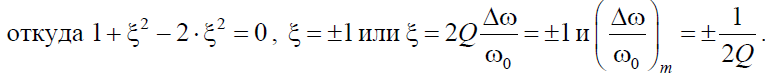
При питании контура от источника тока (источника с бесконечным внутренним сопротивлением) напряжение на контуре

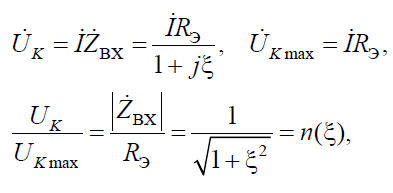
т. е. график функции 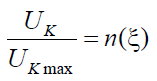имеет вид предельной резонансной кривой, зависящей от соотношений ρ и R, как в последовательном колебательном контуре.

Передаточные функции параллельного контура

Комплексные передаточные функции контура по току

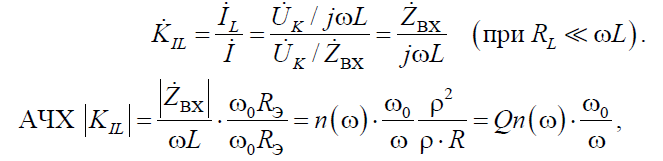
что аналогично АЧХ последовательного контура при выходном напряжении на емкости.

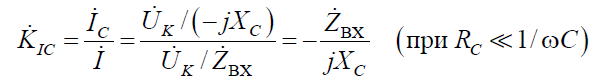
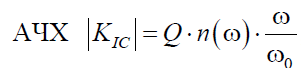что совпадает с выражением для передаточной

функции по напряжению последовательного контура, когда напряжение снимается с индуктивности.

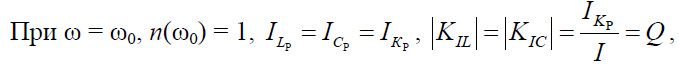
т. е. ток в контуре в Q раз больше тока в неразветвленной части цепи, поэтому явление резонанса называется резонансом токов.