Основы теории цепей
Электрическая цепь. Элементы электрической цепи. Электрические схемы замещения физических устройств идеализированными элементами цепи. Схема электрической цепи (ветвь, узел, контур). Граф цепи.
Электрической цепью называется совокупность устройств, предназначенных для прохождения электрического тока и описываемых с помощью понятий напряжения и тока. Электрическая цепь состоит из источников (генераторов) и потребителей электромагнитной энергии – приемников или нагрузки.
Источником называют устройство, создающее (генерирующее) токи и напряжения. В качестве источников могут выступать устройства (аккумуляторы, гальванические элементы, термоэлементы, пьезодатчики, различные генераторы и т. д.), преобразующие различные виды энергии (химической, тепловой, механической, световой, молекулярно-кинетической и др.) в электрическую энергию. К источникам относятся и приемные антенны, в которых не происходит изменение вида энергии.
Приемником называют устройство, потребляющее (запасающее) или преобразующее электрическую энергию в другие виды энергии (тепловую, механическую, световую и т. д.). К приемникам относятся и передающие антенны, излучающие электромагнитную энергию в пространство. В теории цепей различают активные и пассивные элементы. Активными элементами считаются источники электрической энергии: источники напряжения и источники тока. К пассивным элементам относятся сопротивления, индуктивности и емкости. Цепи, содержащие активные элементы, называются активными, цепи, состоящие только из пассивных элементов – пассивными.
Пассивные элементы. Сопротивлением называется идеализированный элемент цепи, характеризующий преобразование электромагнитной энергии в любой другой вид энергии (тепловую – нагрев, механическую, излучение электромагнитной энергии и др.), т. е. обладающий только свойством необратимого рассеяния энергии. Реальный элемент, приближающийся по своим свойствам к сопротивлению, называется резистором.
Индуктивностью называется идеализированный элемент электрической цепи, характеризующий запасаемую в цепи энергию магнитного поля.
Емкостью называется идеализированный элемент электрической цепи, характеризующий запасаемую в цепи энергию электрического поля. Емкостью между электродами называется отношение потока вектора электрического смещения к разности потенциалов U на зажимах.
Схема электрической цепи
Схемой электрической цепи называется графически изображенная модель ее (рис. 2.1), составленная из идеализированных пассивных (R, L, C) и активных (e, i) элементов. Основными понятиями, характеризующими геометрическую конфигурацию цепи, являются ветвь, узел, контур.
Ветвь – участок цепи, образованный последовательно соединенными элементами. Последовательным соединением элементов цепи называется такое соединение, при котором через них проходит один и тот же ток.
Узел – точка соединения трех и более ветвей.
Контур – любой замкнутый путь, проходящий по нескольким ветвям. Параллельным соединением элементов называется такое соединение, при котором на них действует одно напряжение.
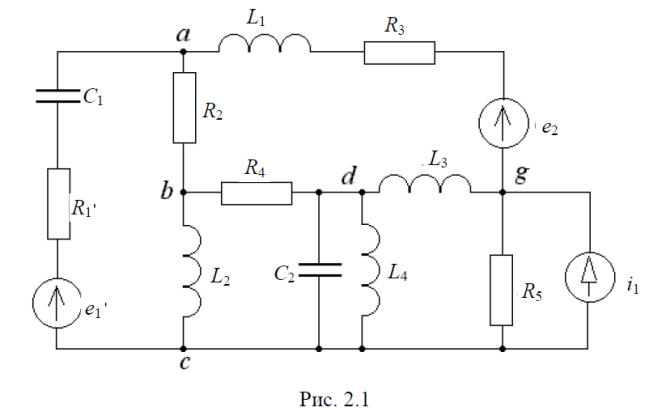
Ветви: ас – C1 R1 e1, аg – L1 R3 e2, ab – R2, bd – R4, dg – L3 и т. д.
Узлы: а, b, c, d, g.
Контуры: 1) a – b – c – a, 2) a – b – d – g – a, 3) b – d – g – c – b и т. д.
Граф цепи.
При исследовании процессов в сложных цепях существенное значение имеет геометрическая структура (топология), характеризуемая совокупностью узлов и ветвей, независимо от конкретных особенностей элементов.
В связи с этим наряду с понятием схемы цепи вводится понятие топологического графа или просто графа (как бы скелета схемы). Если на графе указывают направления токов, то граф называют направленным (рис. 2.2, б). Если граф не может быть изображен без пересечения ветвей, то он называется непланарным (рис. 2.2, в).
Очень важным понятием является так называемое дерево графа – любая система из минимального числа ветвей графа, соединяющая все узлы без образования контуров. Протекание тока по ветвям дерева исключается.
а) б) в)
Рис. 2.2
Таким образом, все ветви графа разбиваются на ветви дерева и не вошедшие в дерево – ветви связи (главные ветви или хорды).
Метод контурных токов
Для сокращения количества уравнений в расчетах токов в цепи часто используется метод контурных токов, являющийся модификацией метода Кирхгофа. При расчете токов этим методом вводят понятие контурного тока как тока в главной ветви независимого контура. Уравнения составляются по второму закону Кирхгофа для независимых контуров, т. е. получается система уравнений с меньшим числом переменных, что является преимуществом метода контурных токов.
Пример:
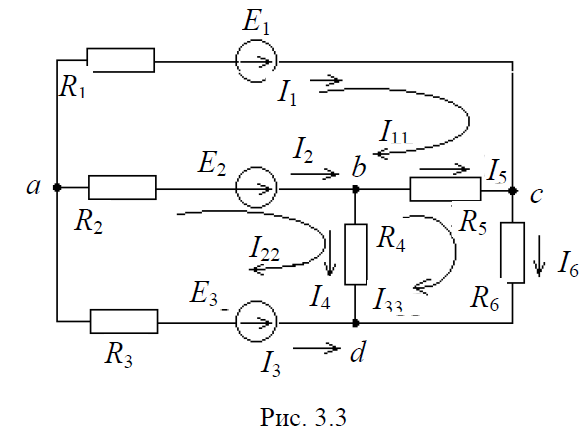
Для схемы (рис. 3.3) имеем:
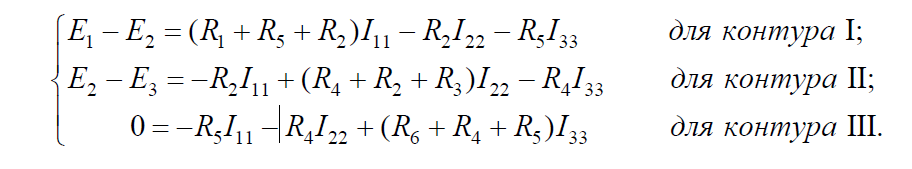
Определив контурные токи из полученной системы уравнений, найдем токи в ветвях:
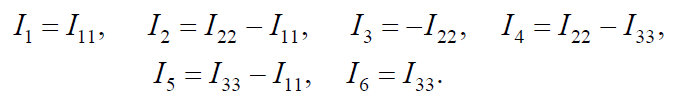
Следует отметить, что при одинаковом направлении контурных токов в системе уравнений суммы сопротивлений, принадлежащих каждому контуру – собственное сопротивление контуров, входят со знаком плюс, а общие сопротивления двух контуров входят со знаком минус.
В общем случае для n-контурной схемы получается n уравнений:
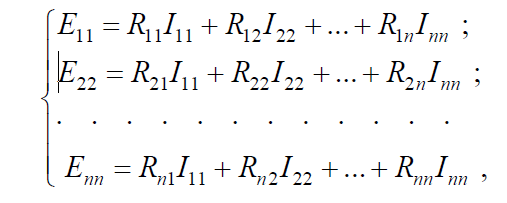
где R11, R22, ..., Rnn – собственное сопротивление контуров;
Rik, ..., Rki – общие сопротивления i-го и k-го контуров.
E11, E22, ..., Enn – контурные ЭДС, алгебраическая сумма ЭДС в каждом контуре.
Решая систему уравнений, находим значения контурных токов. Токи в ветвях находятся как алгебраическая сумма соответствующих контурных токов.
Метод наложения
Ток в любой k-й ветви сложной электрической цепи можно найти, составив уравнения по методу контурных токов, выбрав контуры так, чтобы k-я ветвь входила только в один контур. Тогда ток в k-й ветви будет равен контурному току:
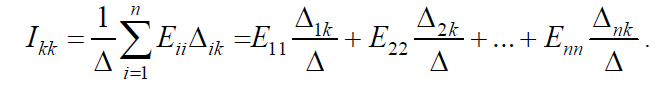
Каждое слагаемое в правой части представляет собой ток, вызванный в k-й ветви соответствующей контурной ЭДС. Например,
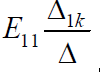 – составляющая тока k-й ветви, вызванная контурной ЭДС E11. Каждая же из контурных ЭДС есть алгебраическая сумма ЭДС ветвей, входящих в соответствующий контур.
– составляющая тока k-й ветви, вызванная контурной ЭДС E11. Каждая же из контурных ЭДС есть алгебраическая сумма ЭДС ветвей, входящих в соответствующий контур.
Таким образом, ток в k-й ветви, создаваемый несколькими источниками ЭДС, включенными в разных участках схемы, равен алгебраической сумме токов, вызываемых каждой из ЭДС в отдельности. Это и есть принцип суперпозиции или наложения.
Этот принцип нашел применение в методе, получившем название «метод наложения». При расчете токов в ветвях цепи поступают следующим образом: поочередно рассчитывают токи, возникающие от действия каждой ЭДС, мысленно удаляя остальные ЭДС из схемы, но оставляя в схеме внутренние сопротивления источников. Ток в ветвях находят как алгебраическую сумму частичных токов от каждого источника.
Если в цепи заданы источники тока и ЭДС, то ток в любой ветви находится также как сумма токов от действия тех и других источников.
Принцип суперпозиции справедлив только для линейных цепей и называется принципом независимости действия, так как базируется на предположении, что каждое слагаемое сложного воздействия на линейную цепь вызывает свой отклик независимо от того, действуют ли в системе другие слагаемые.
Метод узловых напряжений
Метод узловых напряжений является наиболее общим и широко применяется для расчета электрических цепей, в частности в различных программах автоматизированного проектирования электронных схем.
Ток в любой ветви сложной цепи можно найти, определив разность потенциалов между узлами. Метод расчета, основанный на определении напряжений между узлами сложной цепи, называют методом узловых напряжений (узловых потенциалов).
Число неизвестных в этом методе определяется числом уравнений, которые необходимо составить по первому закону Кирхгофа, т. е. метод узловых напряжений тоже является модификацией метода Кирхгофа. Данный метод имеет преимущества по сравнению с методом контурных токов, когда количество узлов меньше числа независимых контуров сложной цепи. Приняв потенциал одного из узлов (базисного или опорного) равным нулю, получим некоторые напряжения остальных узлов относительно базисного, называемые узловыми напряжениями.
Определим токи во всех ветвях цепи (рис. 3.4), приведенной в примере.
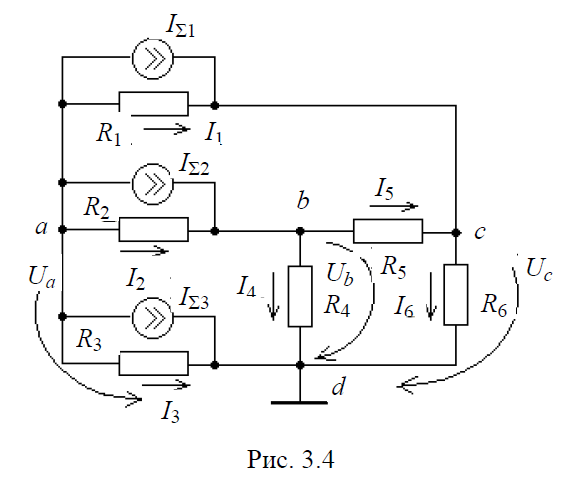
Для узлов a, b, с система уравнений, составленных по первому закону Кирхгофа, следующая
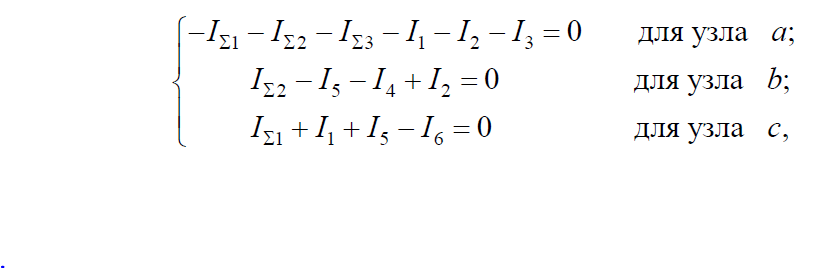
где IΣ1, IΣ2, IΣ3 – токи источников тока.
Токи, протекающие через сопротивления,
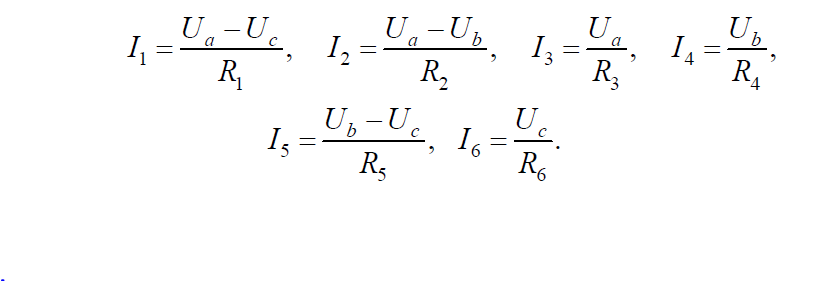
Подставив эти значения в последнюю систему уравнений, получим:
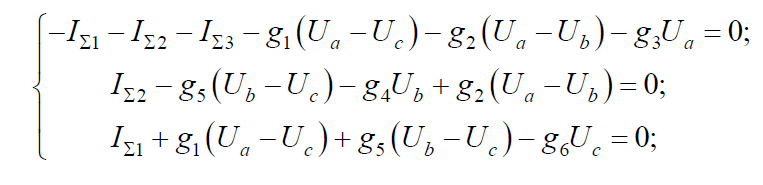
где gk = 1/Rk.
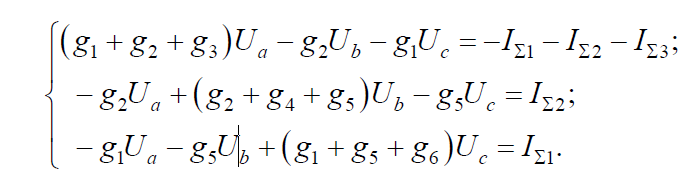
Величины, представляющие собой сумму проводимостей ветвей, сходящихся в данном узле, называются собственной проводимостью узла, величина, равная проводимости ветви между узлами, входящая со знаком минус в систему уравнений, называется общей проводимостью между узлами.
Решив данную систему уравнений, получим узловые напряжения и далее по закону Ома определим токи в ветвях.
В общем случае для сложной цепи, содержащей q узлов:
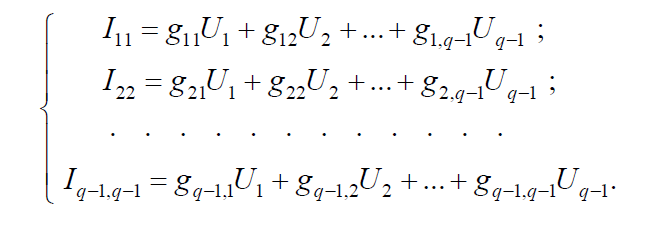
Здесь I11, I22, ..., Iq – 1,q – 1 – алгебраическая сумма токов источников, связанныхс узлами; gii – собственная проводимость i-го узла; gik – общая проводимость между i-м и k-м узлами, входящая со знаком (–) при выбранном направлении узловых напряжений к базисному узлу.
Решив систему уравнений с помощью определителей, получим:
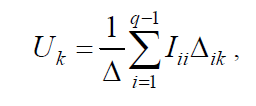
где Δ – определитель системы
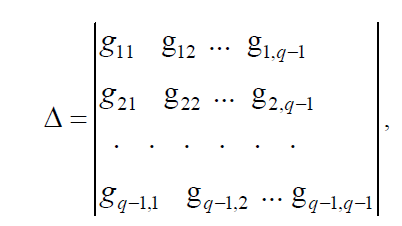
Δik – алгебраическое дополнение элемента gik, полученное из определителя Δ вычеркиванием k-го столбца и i-й строки и умножением полученного определителя на
(– 1)(1 + k).
В развернутом виде:
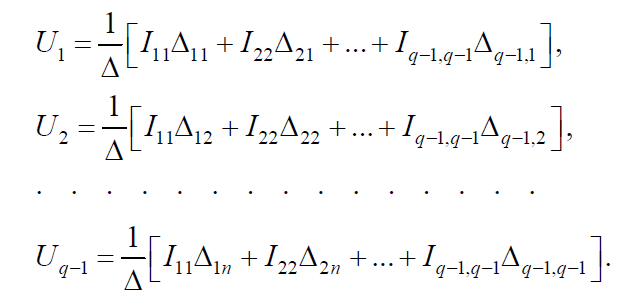
Из последних уравнений следует, что узловые напряжения определяются алгебраической суммой частных узловых напряжений, обусловленных действием каждого источника тока, т. е. как и в методе контурных токов, эти уравнения отражают принцип наложения, характерный для линейных электрических цепей.
Изложенные правила составления узловых уравнений справедливы и для цепей с зависимыми источниками тока, т. е. ИТУН и ИТУТ. В уравнениях появляются дополнительные слагаемые, обусловленные взаимной проводимостью между узлами через зависимые источники.
Активная мощность
Среднее значение мощности за период, равное активной мощности
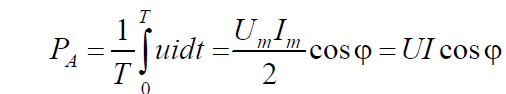
В отличие от цепи, содержащей только активное сопротивление, где
P A = UI = RI2, теперь P A < UI.
Таким образом, активная мощность равна произведению действующих
значений напряжения и тока, умноженному на cos φ, который носит название
коэффициента мощности. Чем ближе угол φ к нулю, ближе cos φ к единице,
тем большая активная мощность будет передаваться от источника к нагрузке
при заданном напряжении.
Реактивная мощность
Мгновенная скорость запасания энергии – реактивная мощность – име-
ет абсолютное значение
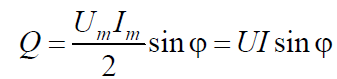
Знак Q свидетельствует о характере запасаемой энергии. Если Q > 0, то
энергия запасается в магнитном поле; если же Q < 0, энергия накапливается в электрическом поле цепи.
В отличие от чисто реактивной цепи, для которой 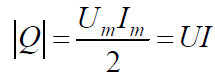 , всмешанной цепи
, всмешанной цепи
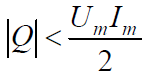
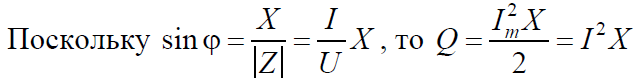
Реактивная мощность измеряется в вольт-амперах реактивных (ВАР).
Реактивная мощность, подводимая к индуктивности,
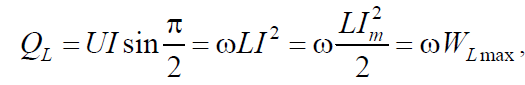
где WL max – максимальное значение энергии магнитного поля, запасаемой в
индуктивности.
Реактивная мощность, подводимая к емкости
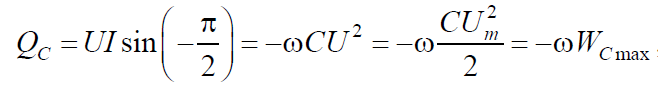
где WC max – максимальное значение энергии электрического поля, запасаемой
емкостью.
В цепи, содержащей индуктивность и емкость, реактивная мощность
Равна Q = ω(WL max - WC max )
Полная мощность
Величина, равная произведению действующих значений напряжения и тока на зажимах цепи S = UI, называется полной мощностью и измеряется в вольт-амперах (ВА).
Поскольку PA = UIcosφ = Scosφ, Q = UIsinφ = Ssinφ, то, очевидно
S2 = PA 2+ Q2 ; tgϕ = Q/PA
Энергетический расчет цепи гармонического тока может быть проведен и методом комплексных амплитуд, если воспользоваться следующим приемом.
Пусть через некоторое комплексное сопротивление Z под действием комплексной амплитуды напряжения
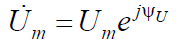
протекает ток с комплексной амплитудой 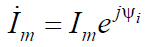
Найдем произведение из комплексной амплитуды напряженияи комплексного числа, сопряженного с комплексной амплитудой тока
Разделив полученное произведение на два, имеем
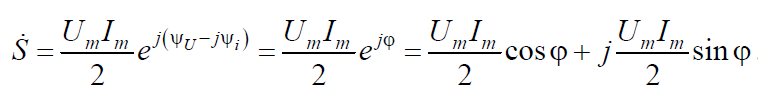
Таким образом, вещественная часть полученного произведения равнаактивной мощности PA, а мнимая часть реактивной мощности Q. На комплексной плоскости соотношение между мощностями может быть представлено в виде треугольника мощностей (рис. 7.3), подобного треугольнику сопротивлений.
Если комплексно-сопряженное напряжение умножить на комплексный ток и поделить полученное произведение на два, то получим:
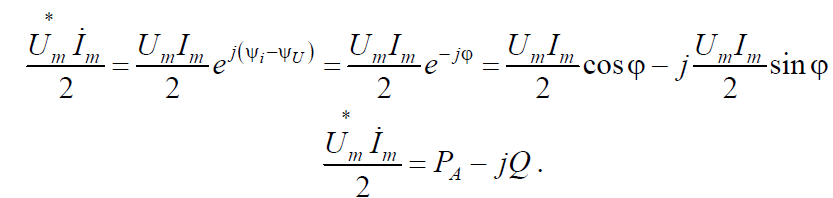
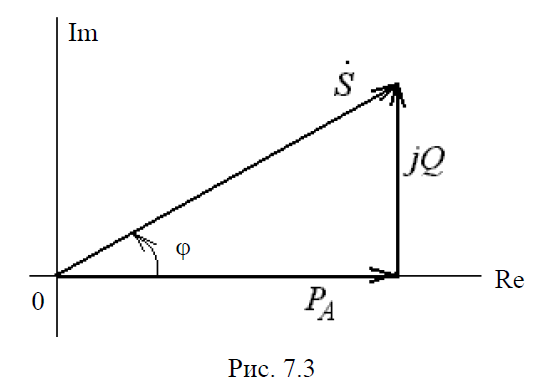
Отсюда следует, что активная и реактивная мощности могут быть записаны в виде
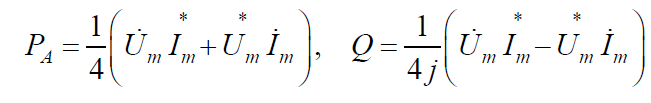
Для комплексов действующих значений напряжения и тока
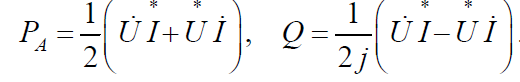
Частотные характеристики
При неизменных E, L, C, R зависимость тока от частоты
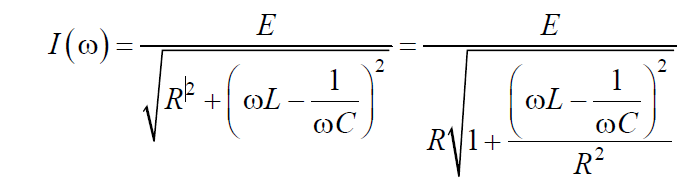
Безразмерное отношение
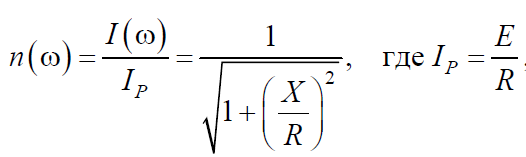
выражает закон изменения амплитуды тока в контуре при изменении частоты (АЧХ) для всех возможных соотношений между X и R и называется предельной нормированной частотной характеристикой контура.
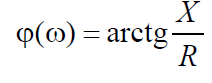 – фазочастотная характеристика контура.
– фазочастотная характеристика контура.
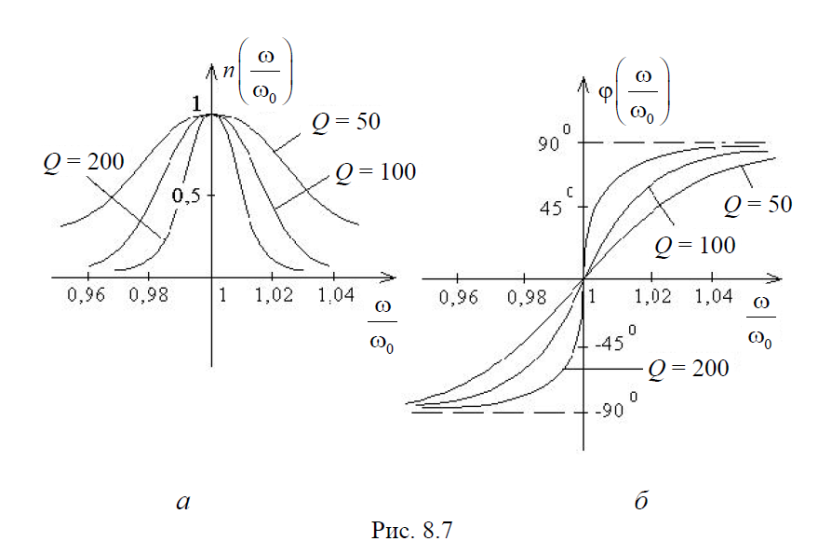
Часто при построении частотных характеристик пользуются нормированными аргументами, например относительной частотой ω/ω0. Тогда для различных соотношений между R и ρ, получим два семейства кривых
(рис. 8.7):
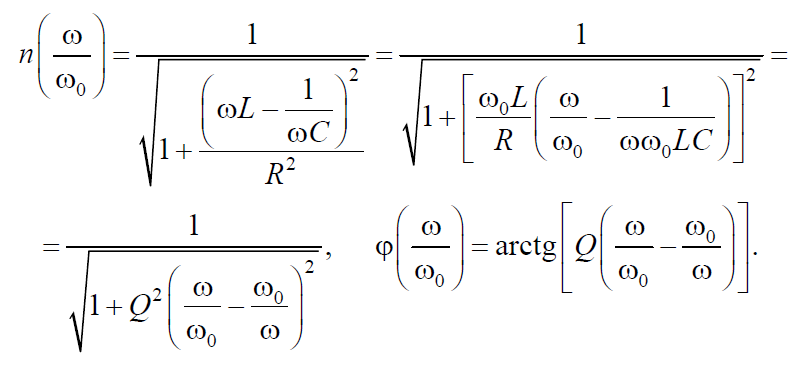
Мостовой четырехполюсник
При анализе и синтезе пассивных симметричных четырехполюсников широко используются мостовые четырехполюсники. Доказано, что для любого пассивного симметричного четырехполюсника можно найти эквивалентный мостовой (рис. 6. а).
Мостовой четырехполюсник можно представить как параллельное соединение двух простых четырехполюсников (рис. 6. б). Уравнения, связывающие напряжения и токи на зажимах этих четырехполюсников, имеют вид
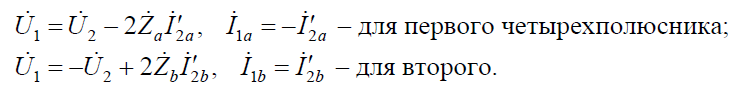
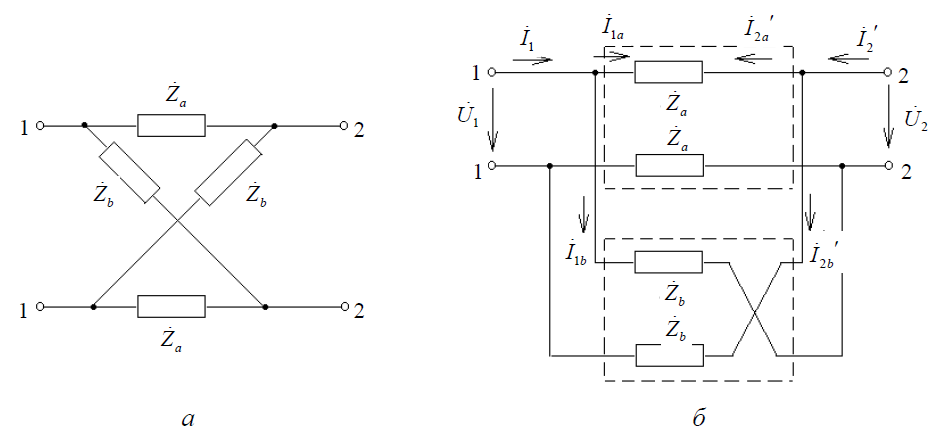
Рисунок 6
С учетом предыдущих выражении, можно получить уравнения для элементарных четырехполюсников
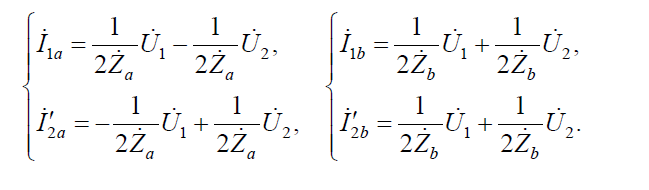
Матрица проводимости мостового четырехполюсника как сумма матриц проводимостей имеет вид
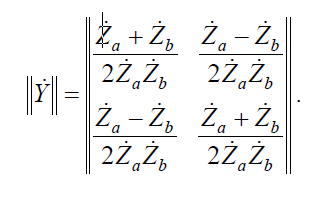
По известным коэффициентам матрицы проводимостей можно найти матрицу А -параметров
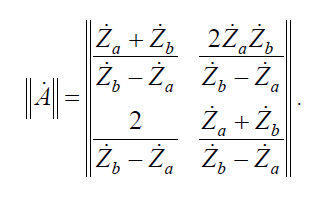
Характеристические параметры симметричного мостового четырехполюсника определяются по формулам:
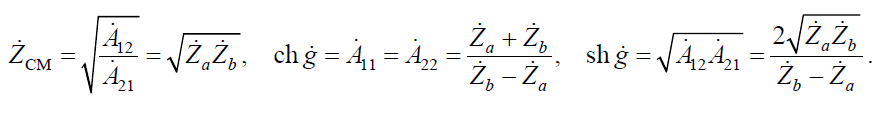
После несложных преобразований получаем
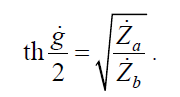
Коэффициент передачи по напряжению мостового четырехполюсника при согласованной нагрузке
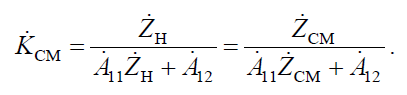
Подставив в эту формулу значения первичных параметров, получим:
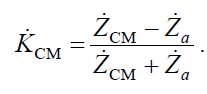
Мостовой четырехполюсник обладает интересными свойствами в том случае, когда элементы 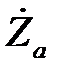 и
и 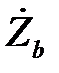 реактивны и имеют разные знаки. Характеристическое сопротивление при этом оказывается вещественным:
реактивны и имеют разные знаки. Характеристическое сопротивление при этом оказывается вещественным:
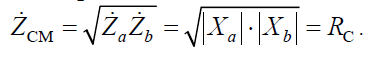
Коэффициент передачи по напряжению реактивного мостового четырехполюсника при согласованной нагрузке
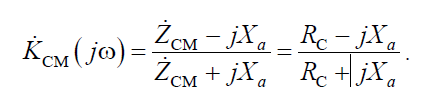
Отсюда видно, что модуль коэффициента передачи 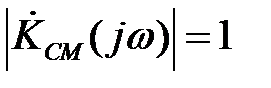 и, значит, такой четырехполюсник пропускает все частоты оез изменения их амплитуд.
и, значит, такой четырехполюсник пропускает все частоты оез изменения их амплитуд.
Фазовый сдвиг напряжений на входе и выходе определяется из формулы
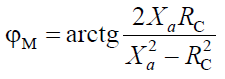
и, следовательно, является функцией частоты. Такие цепи называются четырехполюсниками чисто фазового сдвига и используются при синтезе цепей по заданным частотным характеристикам.
Электроника
По виду проводимости
· Электронные полупроводники (n-типа)
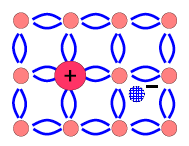
· Полупроводник n-типа
Термин «n-тип» происходит от слова «negative», обозначающего отрицательный заряд основных носителей. Этот вид полупроводников имеет примесную природу. В четырёхвалентный полупроводник (например, кремний) добавляют примесь пятивалентного полупроводника (например, мышьяка). В процессе взаимодействия каждый атом примеси вступает в ковалентную связь с атомами кремния. Однако для пятого электрона атома мышьяка нет места в насыщенных валентных связях, и он переходит на дальнюю электронную оболочку. Там для отрыва электрона от атома нужно меньшее количество энергии. Электрон отрывается и превращается в свободный. В данном случае перенос заряда осуществляется электроном, а не дыркой, то есть данный вид полупроводников проводит электрический ток подобно металлам. Примеси, которые добавляют в полупроводники, вследствие чего они превращаются в полупроводники n-типа, называются донорными.
Проводимость N-полупроводников приблизительно равна:
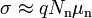
· Дырочные полупроводники (р-типа)
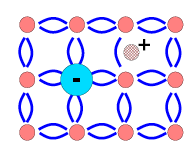
Полупроводник p-типа
Термин «p-тип» происходит от слова «positive», обозначающего положительный заряд основных носителей. Этот вид полупроводников, кроме примесной основы, характеризуется дырочной природой проводимости. В четырёхвалентный полупроводник (например, в кремний) добавляют небольшое количество атомов трехвалентного элемента (например, индия). Каждый атом примеси устанавливает ковалентную связь с тремя соседними атомами кремния. Для установки связи с четвёртым атомом кремния у атома индия нет валентного электрона, поэтому он захватывает валентный электрон из ковалентной связи между соседними атомами кремния и становится отрицательно заряженным ионом, вследствие чего образуется дырка. Примеси, которые добавляют в этом случае, называются акцепторными.
Проводимость p-полупроводников приблизительно равна:
Электронная проводимость
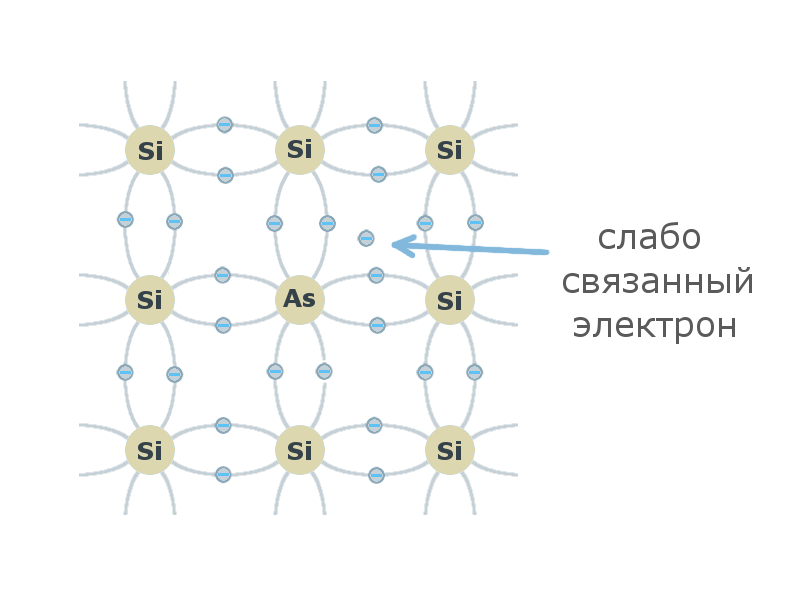
Добавим в полупроводник кремния пятивалентный атом мышьяка (As). Посредством четырех валентных электронов, мышьяк установит ковалентные связи c четырьмя соседними атомами кремния. Для пятого валентного электрона не останется пары, и он станет слабо связанным с атомом.
Под действием электромагнитного поля, такой электрон легко отрывается, и вовлекается в упорядоченное движение заряженных частиц (электрический ток). Атом, потерявший электрон, превращается в положительно заряженный ион с наличием свободной вакансии - дырки.
Несмотря на присутствие дырок в полупроводнике кремния с примесью мышьяка, основными носителями свободного заряда являются электроны. Такая проводимость называется электронной, а полупроводник с электронной проводимостью - полупроводником N-типа.
Дырочная проводимость
Введем в кристалл кремния трехвалентный атом индия (In). Индий установит ковалентные связи лишь с тремя соседними атомами кремния. Для четвертого «соседа», у индия не хватает одного электрона. Этот недостающий электрон может быть захвачен атомом индия из ковалентной связи соседних атомов кремния.
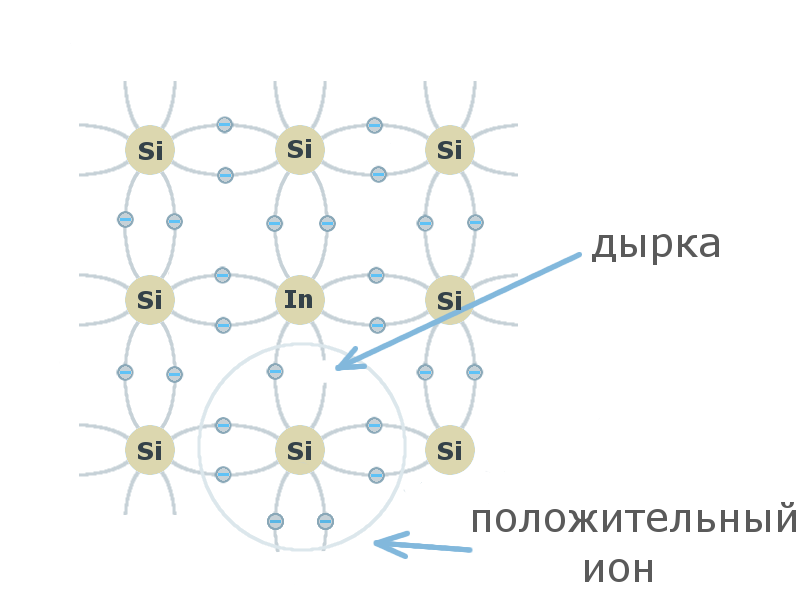
Атом индия превратиться в негативно заряженный ион, а в ковалентной связи соседних атомов образуется вакансия (дырка). В свою очередь, на это место может перескочить электрон из соседней ковалентной связи. В результате получается хаотическое блуждание дырок по кристаллу.
Если поместить полупроводник в электромагнитное поле, движение дырок станет упорядоченным, т.е. возникнет электрический ток. Таким образом, обеспечивается дырочная проводимость. Полупроводник с дырочной проводимостью называется полупроводником P-типа.
Классификация ИС:
По степени интеграции
Кол-во элементов на кристалле K = lg n , где n - число транзисторов
В зависимости от степени интеграции применяются следующие названия интегральных схем:
· малая интегральная схема (МИС) — до 100 элементов в кристалле, К<2
· средняя интегральная схема (СИС) — до 1000 элементов в кристалле,2<K<3
· большая интегральная схема (БИС) — до 10 тыс. элементов в кристалле,2<K<5
· сверхбольшая интегральная схема (СБИС) — более 10 тыс. элементов в кристалле.5<K<6
· ультрабольшая интегральная схема (УБИС) — до 1 млрд элементов в кристалле(K>6) и гигабольшая интегральная схема (ГБИС) — более 1 млрд
Применение
· общего
· специального назначения
Конструктивное исполнение
· корпусные
· безкорпусные
Технология изготовления ИС
Используется групповой метод и пленарная тех-гия.
Групповой - одновременно на одной пластине изгот большое кол-во ИС.
Пленарная тех-гия (плоскостная)- все элем-ты ИС и связи между ними формируются в одной плоскости(реже в 2х или нескольких).
1. Изготовление подложки из кремния
А) необходимо получить кремний и очистить его
Монокристаллические слитки кремнияполучают обычно путем кристаллизации из расплава – методом Чохралъского. При этом методе стержень с затравкой (в виде монокристалла кремния) после соприкосновения с расплавом медленно поднимают с одновременным вращением. При этом вслед за затравкой вытягивается нарастающий и застывающий слиток.
Б) резка слитка на пластины толщиной 0.5мм.
В) шлифование
Г) полировка (механическая, хим-ое травление)
Д) очистка и обезжиривание в органических растворителях
2. Эпитаксия
Эпитаксией называют процесс наращивания монокристаллических слоев на подложку, при котором кристаллографическая ориентация наращиваемого слоя повторяет кристаллографическую ориентацию подложки.
3. Термическое окисление
Окисление кремния – один из самых характерных процессов в технологии современных ИС. Получаемая при этом пленка двуокиси кремния (Si02) выполняет несколько важных функций, в том числе:
· функцию защиты – пассивации поверхности и, в частности, защиты вертикальных участков p–n-переходов, выходящих на поверхность;
· функцию маски, через окна которой вводятся необходимые примеси;
· функцию диэлектрика под затвором МОП-транзистора
4. Легирование
Внедрение примесей в исходную пластину (или в эпитаксиальный слой) путем диффузии при высокой температуре является исходным и до сих пор основным способом легирования полупроводников с целью создания диодных и транзисторных структур
5. Травление
- удаление поверхностного слоя кремния с помощью спец травителей(через маску)
Травители- щелочные(КОН,NaOH);кислотные(HF, HNO3)
Травление- изотропное и анизотропное
6. Фотолитография(масочная технология)
В технологии полупроводниковых приборов важное место занимают маски: они обеспечивают локальный характер напыления, легирования, травления, а в некоторых случаях и эпитаксии. Всякая маска содержит совокупность заранее спроектированных отверстий – окон. Изготовление таких окон есть задача литографии (гравировки). Ведущее место в технологии изготовления масок сохраняет фотолитография.
Фотолитография. В основе фотолитографии лежит использование материалов, которые называют фоторезистами. Это разновидность фотоэмульсий, известных в обычной фотографии. Фоторезисты чувствительны к ультрафиолетовому свету, поэтому их можно обрабатывать в не очень затемненном помещении.
Фоторезисты бывают негативные и позитивные. Негативные фоторезисты под действием света полимеризуются и становятся устойчивыми к травителям (кислотным или щелочным). Значит, после локальной засветки будут вытравливаться незасвеченные участки (как в обычном фотонегативе).
В позитивных фоторезистах свет, наоборот, разрушает полимерные цепочки и, значит, будут вытравливаться засвеченные участки.
7. Нанесение тонких пленок
Существуют три основных метода нанесения тонких пленок на подложку и друг на друга: термическое (вакуумное) напыление, ионно-плазменное напыление и электрохимическое осаждение. Ионно-плазменное напыление имеет две разновидности: катодное напыление и собственно ионно-плазменное.
8. Металлизация
В полупроводниковых ИС процесс металлизации используется для получения омических контактов со слоями полупроводника, а также дорожек проводников и контактных площадок. Основным материалом для металлизации служит алюминий.
9. Сборка и корпусирование.
После того как все основные технологические этапы (включая металлизацию) закончены, пластина кремния, содержащая сотни и тысячи ИС, поступает на операции тестового контроля электрических параметров.
На этом этапе отбраковываются и специальным лаком маркируются все ИС, параметры которых не соответствуют требуемым значениям.
После маркировки отбракованных ИС пластина кремния разделяется на отдельные кристаллы.
Разделение осуществляется методом скрайбирования, т. е., по сути, процарапыванием вертикальных и горизонтальных рисок в промежутках между соседними чипами.
Процарапывание осуществляют либо с помощью алмазного резца (наподобие того, как это делает стекольщик, разрезая стекло), либо с помощью лазерного луча. После скрайбирования пластину разламывают на отдельные кристаллы и годные чипы монтируются в корпусах. Сборка кристалла в корпусе начинается с операции, которую называют посадкой на ножку (под ножкой имеют в виду дно корпуса). При этом кристалл приклеивается или припаивается (легкоплавким припоем) в средней части ножки. Затем контактные площадки на кристалле соединяются со штырьками – выводами корпуса. Соединения осуществляются с помощью тонких (15–30 мкм) алюминиевых или золотых проволочек, которые одним концом закрепляются на контактных площадках, а другим – на торцах штырьков.
Надежный электрический контакт между металлическими деталями (в данном случае контакт проволочек со штырьками и контактными площадками) может быть обеспечен разными методами. Наибольшее распространение в настоящее время имеет метод термокомпрессии, т. е. сочетание достаточного давления (прижатия деталей друг к другу) с повышенной температурой (200–300 °С), способствующей взаимной диффузии атомов из одной детали в другую.
По окончании монтажа кристалла на ножке следует корпусирование, т. е. окончательное внешнее оформление транзистора. Ножка корпуса соединяется с крышкой (рис. 19.6) путем горячей или холодной сварки (последняя по существу близка к термокомпресии). Корпусирование предполагает также защиту кристалла от влияния внешней среды, поэтому его проводят либо в вакууме, либо в среде инертного газа (азот, аргон).
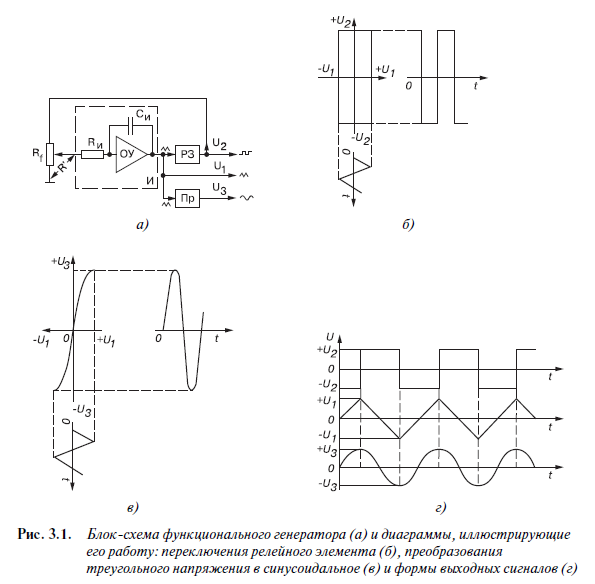
Функциональный генератор (ФГ) синусоидальных, треугольных и прямоугольных сигналов. Структурная и принципиальная схемы ФГ на ОУ.
Функциональными генераторами принято называть генераторы нескольких функциональных зависимостей (сигналов), например, прямоугольных, треугольных и синусоидальных, формируемых с одной перестраиваемой в достаточно широких пределах частотой [8,91). Разнообразие форм сигналов расширяет сферы применения таких генераторов и позволяет использовать их для тестирования, отладки и исследования самой разнообразной электронной аппаратуры.
В отличие от RC- и 1С-генераторов функциональные генераторы являются более широкодиапазонными — отношение максимальной частоты генерации к минимальной у них имеет нередко порядок 10s— 106и выше. Наиболее часто функциональные генераторы используются при отладке ВЧ. НЧ и сверхнизкочастотных устройств. В СВЧ- диапазоне частот эти устройства не используются, за исключением применения в качестве источников модулирующих сигналов.
Функциональные генераторы делятся на два широких класса:
Аналоговые функциональные генераторы на основе интегратора аналоговых сигналов в виде прямоугольных импульсов (меандра).
Цифровые функциональные генераторы на основе дискретных (цифровых) интеграторов.
Помимо простоты реализации, аналоговые функциональные генераторы имеют одно неоспоримое преимущество перед их цифровыми собратьями — отсутствие ступенек на участках роста и спада пилообразного и синусоидального выходных напряжений. Это особенно важно, если необходимо получение производной от выходного напряжения генератора. В этом случае ступеньки недопустимы, поскольку при переходе от одной ступеньки к другой производная устремляется к очень большим значениям.
Для реализации аналогового интегрирования применяют устройства заряда-раз- ряда конденсатора неизменным током и схемы со 100% отрицательной обратной связью (емкостные интеграторы на интегрирующих усилителях постоянного напряжения).
Широкое распространение аналоговые функциональные генераторы получили после разработки высококачественных интегральных операционных усилителей, на которых стало возможно построение прецизионных интеграторов. Они и составляют основу функциональных генераторов. К сожалению, максимальная частота у таких генераторов обычно не превосходит 1—3 МГц и ограничена частотными свойствами применяемых операционных усилителей. Функциональные генераторы на основе заряда- разряда конденсатора с одной заземленной обкладкой реализуют максимальные частоты до 20—30 М Гц.
Теория электрических связей
Спутниковая связь
Спутниковые линии (СЛ) используют сантиметровый диапазон волн. Отличие от РРЛ в том, что ретранслятор поднят на околоземную орбиту.
Все существующие спутники можно разделить на спутники низкой, средней околоземной орбиты и геостационарные спутники. Высота геостационарной орбиты составляют 36 000 км, на этой орбите спутник вращается с угловой скоростью Земли. Три спутника под углом 1200 способны обеспечить связью всю планету.
| Земля |
Рис. 9.15. – Охват Земли тремя геостационарными спутниками
Спутниковые линии связи применяют для:
- вещания ТВ программ;
- связи с удаленными труднодоступными районами (крайний Север, дальный Восток);
- для военных нужд.
Стоимость канала спутниковой линии достаточно высока, большую часть стоимости составляет запуск спутника.
Классификация спутников:
1. По зоне обслуживания:
- глобальные;
- региональные;
-национальные.
2. По типу услуг:
- стационарная служба связи (fixed service satellite - FSS);
- радиовещательная служба связи (broadcast service satellite - BSS);
- мобильная служба связи (mobile service satellite - MSS).
3. По характеру использования:
- коммерческие;
- военные;
- любительские;
-экспериментальные.
Классификация орбит:
1. По форме:
- круговая;
- эллиптическая.
2. По плоскости:
- экваторивальная;
- полярная;
- наклонная.
3. По высоте над уровнем моря:
- геостационарные околоземные орбиты (geostationary earth orbit - GEO);
- средние околоземные орбиты (medium earth orbit - MEO);
- низкие околоземные орбиты (low earth orbit - LEO).
Геостационарные спутники
Высота орбиты составляет 35863 км. Число геостационарных спутников на орбите достигло того, что спутники располагаются на орбите достаточно близко друг к другу. Круговая орбита проходит вдоль экватора Земли.
Достоинства геостационарной орбиты:
- отсутствие эффекта Доплера (изменение частоты сигнала при относительном движении спутника и антенн, т.к. спутник неподвижен относительно Земли);
- упрощенная процедура отслеживания;
- простота в покрытии больших территорий.
Недостатки геостационарной орбиты:
- серьезное ослабление сигнала (большие расстояния);
- полярные области северного и южного полюсов практически недоступны;
- большая задержка при прохождении сигнала, ок. 0,12 секунд в одном направлении и это только для абонентов на экваторе. На территории задержка больше;
- из-за большого охвата территории имеется низкое использование полосы частот. Т.е. всей полосой спутника пользуются все охватываемые им территории, что плохо для многоточечных приложений (телефонная связь), но хорошо для вещательных.
Большинство недостатков присущих спутникам работающим на геостационарной орбите лишены спутники работающие на средней и низкой околоземной орбитах.
Свойства дисперсии
Дисперсия постоянной величины с равна нулю.
Доказательство: по определению дисперсии
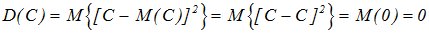
При прибавлении к случайной величине Х неслучайной величины с ее дисперсия не меняется.
D[X+c] = D[X].
Доказательство: по определению дисперсии
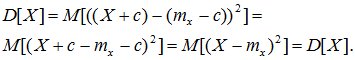 (6.12)
(6.12)
3. При умножении случайной величины Х на неслучайную величину с ее дисперсия умножается на с2.
Доказательство: по определению дисперсии
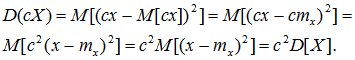 . (6.13)
. (6.13)
Для среднего квадратичного отклонения это свойство имеет вид:
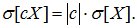 (6.14)
(6.14)
Действительно, при ½С½>1 величина сХ имеет возможные значения (по абсолютной величине), большие, чем величина Х. Следовательно, эти значения рассеяны вокруг математического ожидания М[сХ] больше, чем возможные значения Х вокруг М[X], т.е. 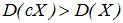 . Если 0<½с½<1, то
. Если 0<½с½<1, то 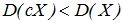 .
.
Правило 3s. Для большинства значений случайной величины абсолютная величина ее отклонения от математического ожидания не превосходит утроенного среднего квадратического отклонения, или, другими словами, практически все значения СВ находятся в интервале:
[ m - 3s; m + 3s; ].(6.15)
Коэффициент корреляции.
Величина cov(x;h) зависит от единиц измерения, в которых выражаются x и h. (Например, пусть x и h—линейные размеры некоторой детали. Если за единицу измерения принять 1 см, то cov(x;h) примет одно значение, а если за единицу измерения принять 1 мм, то cov(x;h) примет другое, большее значение (при условии cov(x;h)¹0)). Поэтому cov(x;h) неудобно принимать за показатель связи.
Чтобы иметь дело с безразмерным показателем, рассмотрим случайные величины
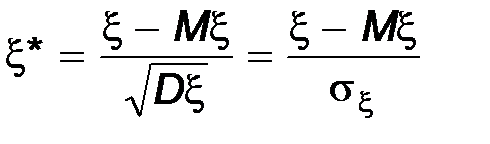 ;
; 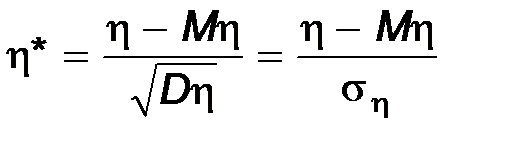
Такие случайные величины называются нормированными отклонениями случайных величин x и h.
Каждая из случайных величин x* и h* имеет центром (математическое ожидание) нуль и дисперсию, равную единице. Приведём доказательство для случайной величины x*.
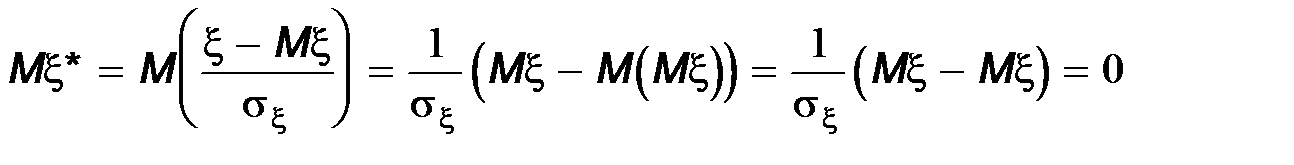
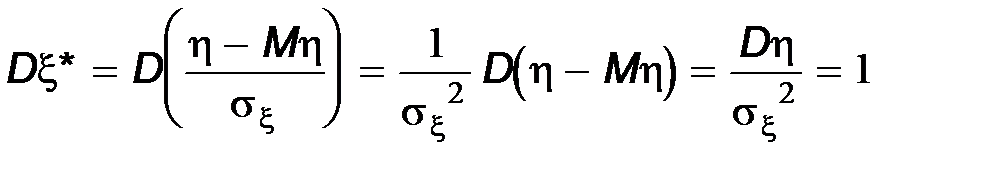
Ковариация x* и h* называется коэффициентом корреляции случайных величин x и h (обозначается rxh).
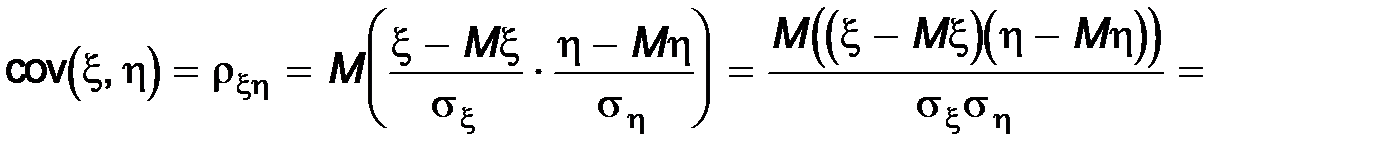
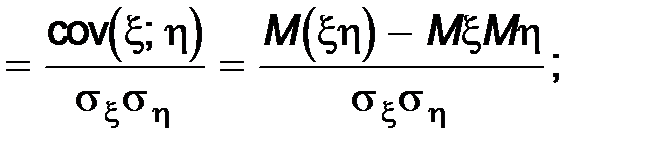
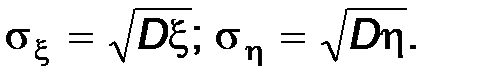
Для независимых x и h rxh=0, так как в этом случае cov(x;h)=0
Обратного заключения сделать нельзя. Случайные величины могут быть связаны даже функциональной зависимостью (каждому значению одной случайной величины соответствует единственное значение другой случайной величины), но коэффициент их корреляции будет равен нулю.
Свойства коэффициента корреляции.
1. –1£rx h£1
2. Если rx h=1, то h=kx+b, где k и b—константы, k>0.
3. Если rx h= –1, то h= kx+b, где k<0.
4. Если h=kx+b, (k ¹0) или x=k 1h+b1, то
rx h=1 при k>0
rx h= – 1 при k<0.
Коэффициент корреляции rx h достигает своих предельных значений –1 и 1 в том и только в том случае, если совместное распределение x и h все концентрируется на некоторой прямой в плоскости x; h, то есть между x и h имеется такая линейная зависимость.
Если êrxhê<1, то такой линейной зависимости нет. Все же по мере приближения êrxhê к единице совместное распределение x; h имеет тенденцию концентрироваться вблизи некоторой прямой линии и величину êrxhê можно считать мерой близости к полной линейной зависимости между x и h.
Помехи в каналах связи.
Помеха – посторонний электрический сигнал мешающий приему сигнала.
Сигнал на входе приемника = сигнал на выходе передатчика + помеха
Помехи делятся:
По источнику возникновения – внутренние, внешние
По спектру – со сплошным спектром, ……….
По структуре – флуктоационные (непрерывные), импульсные
По воздействию – Аддитивная, Мультипликативная
Аддитивная помеха – помеха складывается с сигналом
Мультипликативная помеха – помеха умножается с сигналом
Мультипликативная помеха и Аддитивная помеха могут сочитаться
AWGN (аддитивный белый гауссовский шум) – шум вызванный движением носителей заряда (любой металл является источником небольшой ЭДС) имеет сплошной спектр, закон распределения плотности вероятностей –нормальный (гауссовский).
Пропускная способность непрерывного канала связи с помехой.
| Канал связи |
x(t) y(t)
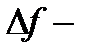 полоса частот канала сигналов x(t) и y(t).
полоса частот канала сигналов x(t) и y(t).
n=2 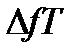 .
.
Скорость передачи для непрерывного сигнала определяется так же как и для дискретного:
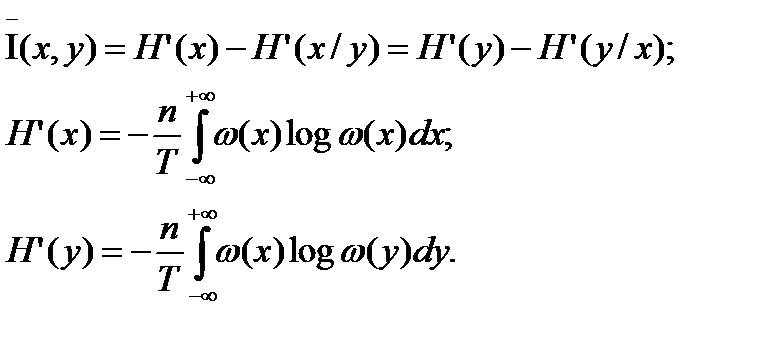
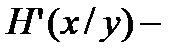 ненадёжность канала связи по времени.
ненадёжность канала связи по времени.
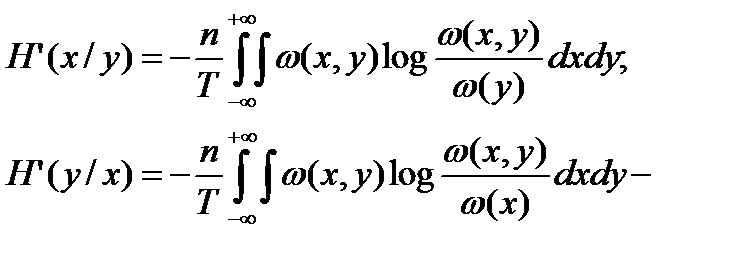
энтропия выходного сигнала относительно входного в единицу времени.
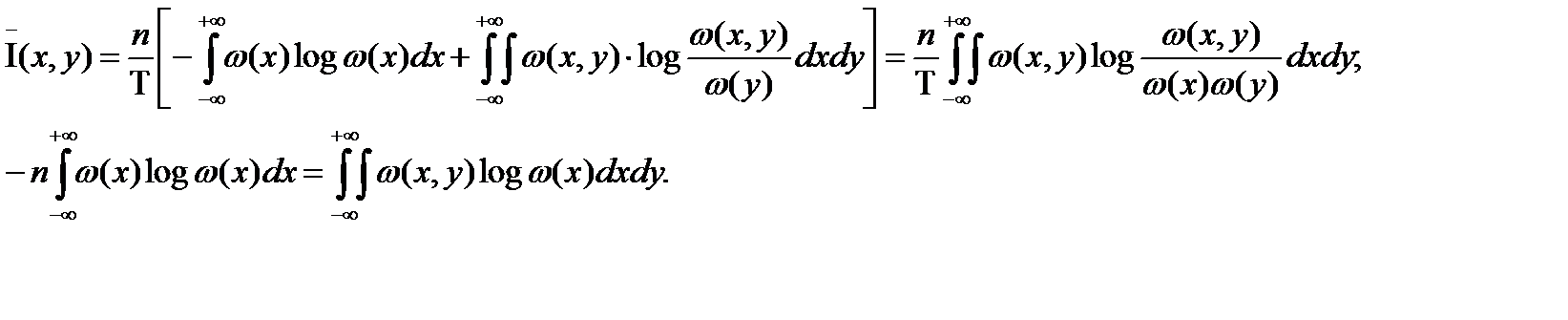
Максимизируем 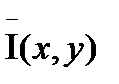 , чтобы получить пропускную способность:
, чтобы получить пропускную способность:
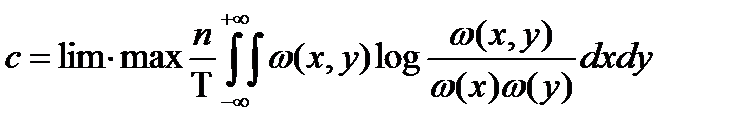 Þ пропускная способность канала равна 0, если входные и выходные сигналы независимы.
Þ пропускная способность канала равна 0, если входные и выходные сигналы независимы.
Если входной сигнал и помеха независимы и помеха является аддитивной, то скорость передачи равна энтропии выходного сигнала за вычетом энтропии помехи за единицу времени: 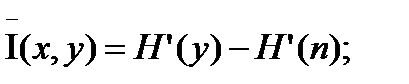
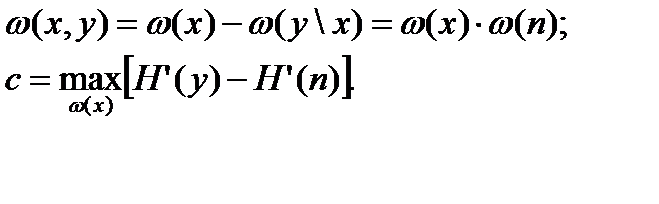
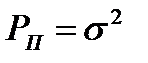 -мощность помехи.
-мощность помехи.
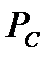
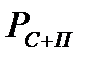
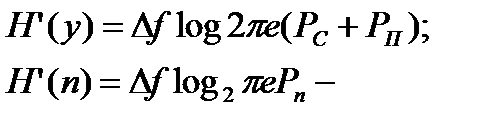
энтропия помехи.
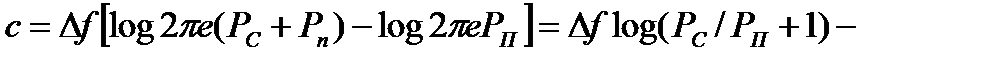 пропускная способность.
пропускная способность.
ПОЛУЧЕНИЕ
Для получения АМ колебаний самое простое это подавать модулирующий сигнал на усилитель, в который встроен свой генератор высокой частоты, который собственно и создает несущее колебание. Принципиальные схемы там вот кароче:
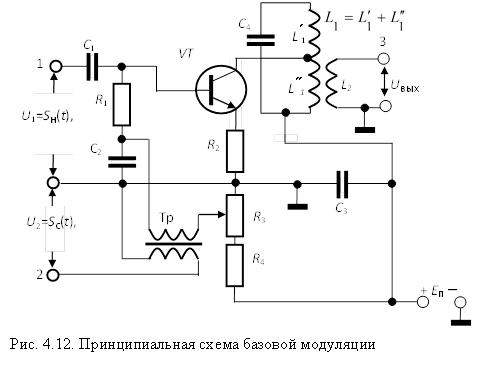
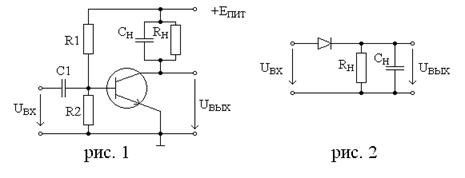
Кароче там вся херня заключается в том, что когда на базу подается какое-то напряжение или ток, карчое этот сигнал открывает транзистор пропорционально величине поданного напряжения или тока, ну и кароче через транзистор ток ебашит с амплитудой, зависящей от степени открытости транзистора. Типа того. Если кароче снимать выходной сигнал с коллектора, то там при закрытом транзисторе напряжение равно тому, которое подали на коллектор, а при открытом там транзистор превращается в короткое замыкание и напряжение падает. Кароче по сути получается инвертирование напряжения, но это не страшно.
Алсо через транзистор ебашит ток гармонический же там, синусоидой. Это реализуется колебательным контуром, вставленным как на схемах например.
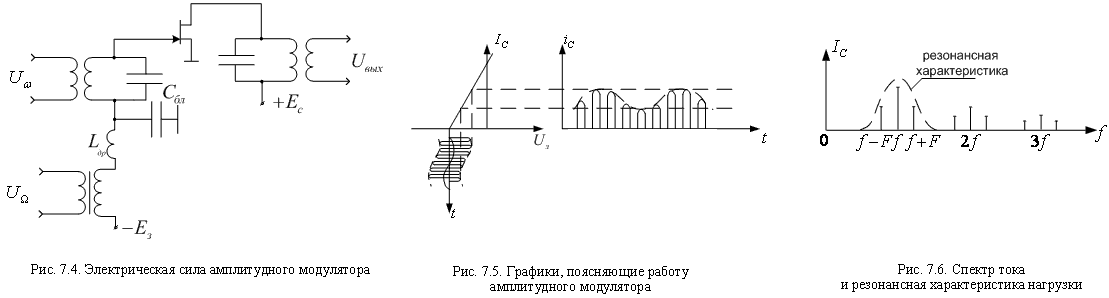
|
Ну кароче это вот собственно графики, показывающие то что там в подписи у них написано азазаза.
Ниже описывается такая фигня, как пороговое напряжение при открытии транзистора. НУ типа шобы его открыть надо определенной величины сигнал подать. Ну и там можно изначально подать дофига большое напряжение например, а транзистор не откроется, т.к. потенциал на базе изначально низкий слишком например. Поэтому его обычно выравнивают резисторами, шобы поданый сигнал там при минимальных значениях своих открывал транзюк. Ну и да кстати у транзюка есть своя амплитудная характеристика ну типа он же дофига бесконечно открываться не может. Если слишком сильный сигнал подать, у него будут скошеные верхние горбы дофига, что есть либо плохо, либо дисторшн для гитарки. Надо выбирать участок полинейнее.
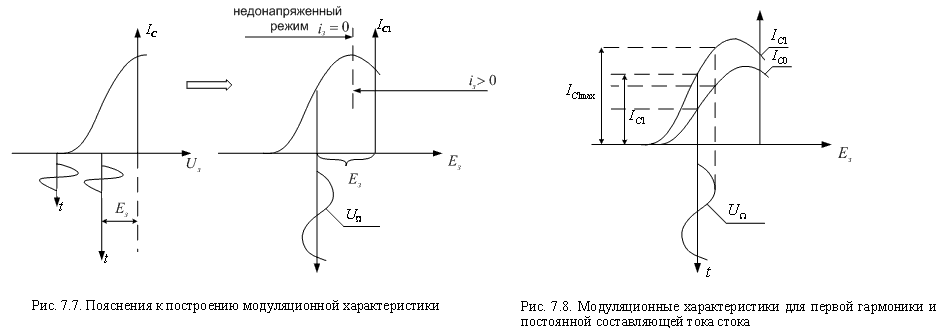
ДЕТЕКТИРОВАНИЕ
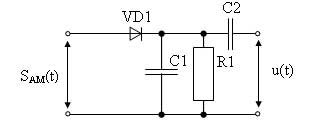
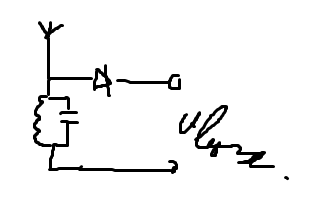
Рисунок 41 - Принципиальная электрическая схема некогерентного амплитудного детектора на диоде
Детектируется в простейшем случае херней на правом рисунке (на левом там с фильтром нижних частот еще (С1, R1)). Ну и кароче через антенну на колебательном контуре создаются колебания, и их амплитуда как раз изменяется по закону модулирующего сигнала. Диод кароче нужен ща скажу зачем:
На рисунках пониже есть график левый верний. На нем там типа гармоника с амплитудами сверху и снизу. Ну нам кароче нафиг не надо две зеркальные амплитуды и мы нижнюю отрезаем. Фильтр кароче нижних частот (как на рисунке сверху) нужен потому шо при отрезании нижних амплитуд сигнал множится по блин… забыл… по гармоникам чтоли. Ну и кароче это нафиг не надо. Надо нам только низкочастотный информационный сигнал. Мы его и пропускаем. Получается тупо низкочастотный сигнал, НО с постоянно составляющей, ибо поднят выше нуля постоянно. В этом нам помогает конденсатор С2, который это дерьмо выпиливает. Получаем инфу изначальную. 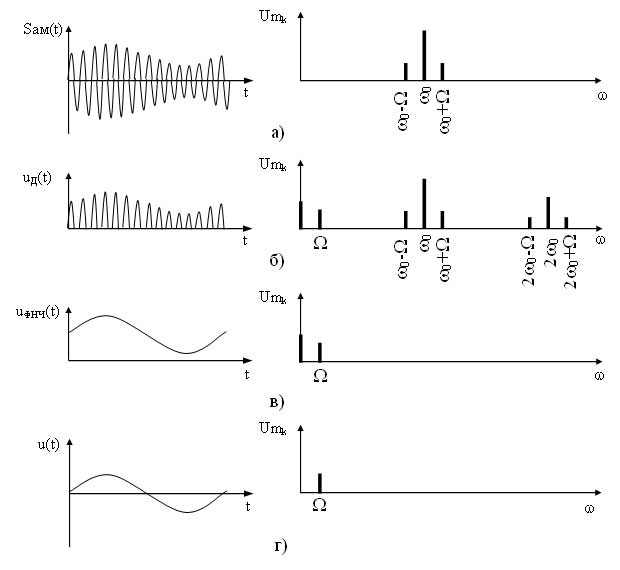 Рисунок 42 - Процесс детектирования АМ сигналов
Рисунок 42 - Процесс детектирования АМ сигналов

Рисунок 42 - Процесс детектирования АМ сигналов
Детектирование ЧМ сигналов
Кароче как вариант: принимать ЧМ сигнал АЧМ детектором. Как говорится, вот он:
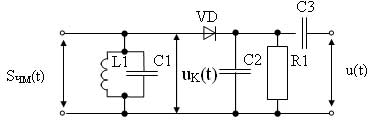
Рисунок 46 - Принципиальная электрическая схема однотактного частотного детектора
Кароче говоря все пляшет от АЧХ контура. Обозначена на рисунке ниже горбом интересным:
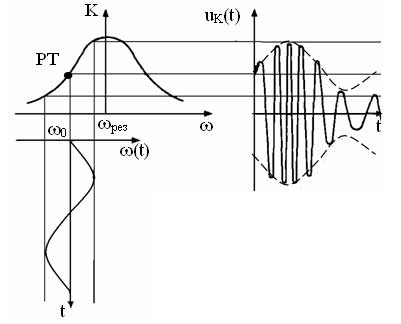
Рисунок 47 - Временные диаграммы частотного детектора
Если карчое частота сигнала чутка отклоняется от частоты контура, то он какбе это сигнал и пропускает поменьше, выдавая какбы ту же регонансную гармонику, но с другой амплитудой. Таким образом ФМ сигнал перелопачивается в АМ ну и там дальше АМ детектором детектируется.
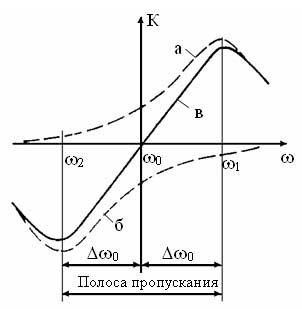
Детекторная характеристика этого детектора является нелинейной и приутствуют некоторые нелинейные искажения, для устранения которых используют двухтактную схему частотного детектора с двумя контурами, расстроенными чутка относительно друг друга. Ну и сложение их АЧХ там уже выдает более линейную общую АЧХ типа.
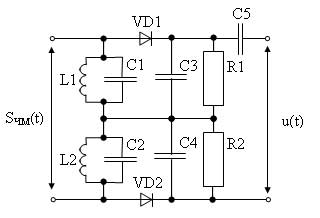
| 
|
| Рисунок 49 - балансный частотный детектор | Рисунок 50 - Частотная зависимость колебательных контуров балансного детектора |
При ЦАМ
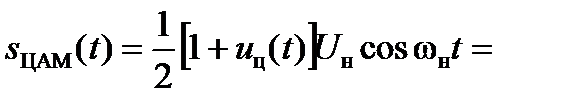
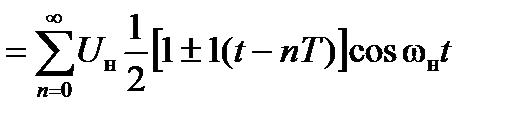 , (3.15)
, (3.15)
При ЦФМ
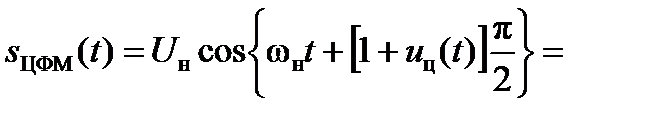
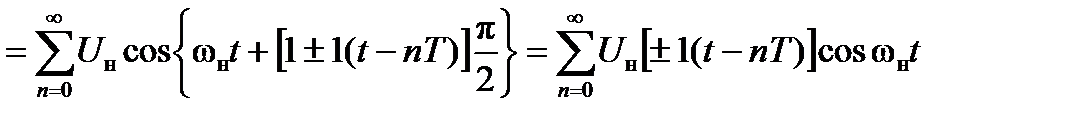
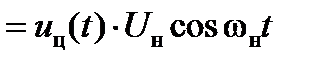 , (3.16)
, (3.16)
При ЦЧМ
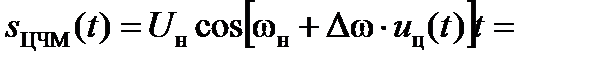
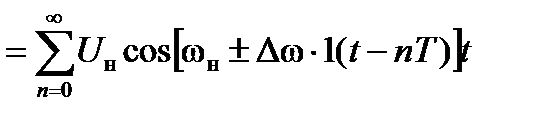 , (3.17)
, (3.17)
где девиацию частоты Dw выбирают из условия обеспечения ортогональности сигналов s0(t) и s1(t).
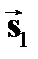 ЦАМ ЦЧМ ЦФМ
ЦАМ ЦЧМ ЦФМ
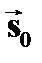 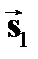 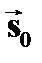 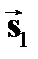 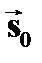 0 0 0
Рис. 3.47. Векторы
0 0 0
Рис. 3.47. Векторы 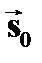 и и 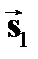 при цифровой модуляции при цифровой модуляции
|
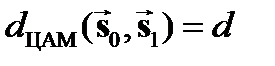 ,
, 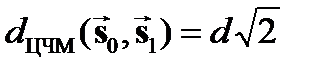 ,
, 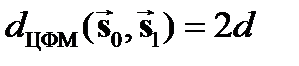 .
.
Очевидно, что чем больше расстояние между сигналами, тем они надёжнее различаются при приёме на фоне помех. Следовательно, наибольшей помехоустойчивостью обладает ЦФМ, а наименьшей ЦАМ. Реализация модуляторов сигналов с ЦМ не вызывает сложностей и вытекает из аналитиче ских выражений соответствующих Общим недостатком рассмотренных простых видов ЦМ является низкая скорость передачи 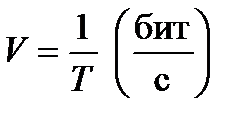 . Для её повышения прибегают к увеличению объёма алфавита кода m
. Для её повышения прибегают к увеличению объёма алфавита кода m
Импульсная модуляция.
Часто в качестве переносчика используют периодическую последовательность сравнительно узких импульсов. Последовательность прямоугольных импульсов одного знака v 0 ( t ) характеризуется параметрами (рис. 3.22.1): амплитудой импульсов V , длительностью (шириной) импульсов τи; частотой следования (или тактовой частотой) fT =1/ T, где Т – период следования импульсов (ωT = 2πfT ); положением (фазой) импульсов относительно тактовых (отсчетных) точек. Отношение T /τи называется скважностью импульса.
Рис. 3.22.1. – Последовательность прямоугольных импульсов
По закону передаваемого первичного сигнала можно изменять (модулировать) любой из перечисленных параметров импульсной последовательности. При этом модуляция называется импульсной.
Рис. 3.22.2. а, б, в, г, д – Варианты импульсной модуляции
В зависимости от того, какой параметр модулируется первичным сигналом s ( t ), различают: амплитудно-импульсную модуляцию (АИМ), когда по закону передаваемого сигнала (рис. 3.22.2. а) изменяется амплитуда импульсов (см. рис. 3.22.2. б); широтно-импульсную модуляцию (ШИМ), когда изменяется ширина импульсов (рис. 3.22.2. в); частотно-импульсную модуляцию (ЧИМ) - изменяется частота следования импульсов (рис. 3.22.2. г); фазо-импульсную модуляцию (ФИМ) – изменяется фаза импульсов, т.е. временное положение относительно тактовых точек (рис. 3.22.2. д). Модуляцию ФИМ и ЧИМ объединяют во временно-импульсную (ВИМ). Между ними существует связь, аналогичная связи между фазовой и частотной модуляцией синусоидального колебания.
В качестве примера на рис. 3.22.3 показан спектр АИМ-сигнала при модуляции импульсной последовательности сложным первичным сигналом s ( t ) с полосой частот от 0 до Ω. Он содержит спектр исходного сигнала s ( t ), все гармоники тактовой частоты ωT (т.е. частоты 2ωТ, ЗωТ, 4ωТ и т.д.) и боковые полосы частот около гармоник тактовой частоты.
Рис. 3.22.3. – Спектр АИМ-сигнала
Спектры сигналов ШИМ, ЧИМ и ФИМ имеют еще более сложный вид.
Импульсные последовательности, изображенные на рис. 3.22.2. а, б, в, г, д, называются последовательностями видеоимпульсов. Если позволяет среда распространения, то видеоимпульсы передаются без дополнительных преобразований (например, по кабелю). Однако по радиолиниям передать видеоимпульсы невозможно. Тогда сигнал подвергают второй ступени преобразования (модуляции).
Модулируя с помощью видеоимпульсов гармоничное несущее колебание достаточно высокой частоты, получают радиоимпульсы, которые способны распространятся в эфире. Полученные в результате сочетания первой и второй ступеней модуляции сигналы могут иметь названия АИМ-АМ, ФИМ-АМ, ФИМ-ЧМ и др.
Каналы связи. Канал с аддитивным шумом. Линейный стационарный (фильтровой) канал. Линейный нестационарный канал. Случайный линейный канал. Канал со случайными затуханием и задержкой. Канал с многолучевым распространением. Нелинейный канал. Дискретно-непрерывные каналы. Дискретные каналы.
Классификация каналов

 Канал с аддитивным шумом
Канал с аддитивным шумом 
Канал со случайными затуханием и задержкой ( на примере оптического канала связи)

Канал с многолучевым распространением.

Дискретные каналы


Дискретно-непрерывные каналы

Линейные и нелинейные модели каналов связи
Cвязь сигналов (в общем случае многомерных, векторных) на входе x(t) и выходе y(t).
Пишем просто формулу без хрени справа

Система стационарна, если её отклик на выходе не зависит от того, в какой момент времени поступает входной сигнал. Стационарные системы называют системами с постоянными во времени параметрами.
Если свойства системы зависят от того, в какой момент времени поступает входной сигнал, систему называют нестационарной (системой с переменными во времени параметрами или параметрической системой).
Важнейший принцип классификации систем (каналов) основан на том, что различные системы по-разному реагируют на сумму нескольких сигналов.

Детерминированная безынерционная одномерная нелинейная модель — сигналы на выходе y(t) и входе канала x(t) связаны соотношением:

ДНА. Виды и параметры ДН.
ДН по полю называют зависимость амплитуды поля от пространственных углов 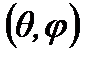 при неизменных условиях наблюдения и возбуждения. Нормированная ДН.
при неизменных условиях наблюдения и возбуждения. Нормированная ДН.
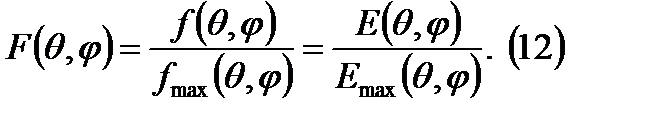
ДН по мощности называется зависимость плотности потока излучаемой мощности от пространственных углов 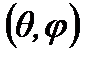 при неизменных условиях наблюдения и возбуждения. Нормированная ДН.
при неизменных условиях наблюдения и возбуждения. Нормированная ДН.
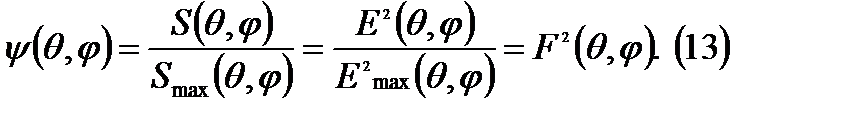
Нормированная ДН обеспечивает облегчение сравнения направленных свойств различных антенн.
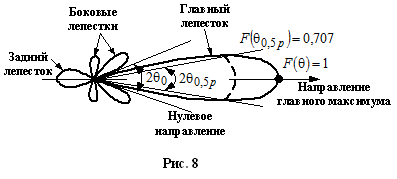 ДН имеет сложную многолепестковую структуру.
ДН имеет сложную многолепестковую структуру.
ДН характеризуют формой главного лепестка и шириной ДН в двух взаимно перпендикулярных плоскостях.
К параметрам ДН любой антенны мы можем отнести:
1) Вид ДН
2) Ширину ДН в двух ортогональных плоскостях
3) Уровень боковых лепестков.
Ширину ДН могут измерять по уровню половинной мощности 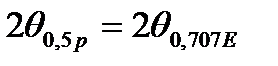 (0,707 по Амплитуде) или по нулевому уровню
(0,707 по Амплитуде) или по нулевому уровню 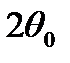 . Как правило ширину ДН измеряют по
. Как правило ширину ДН измеряют по 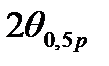 .
.
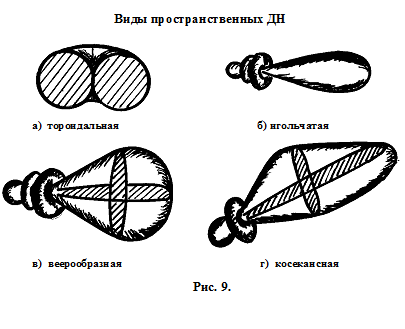 Тороидальная(если вращать элементарный электрический или симметричный вибратор)
Тороидальная(если вращать элементарный электрический или симметричный вибратор)
Игольчатая – как ручка(ширина в обеих плоскостях одинаковая).
Веерная - в одной плоскости широкая в другой узкая. Используется в дальномерах.
Косекансная(спец вида) используется в радиолокации.
От выбора ДН зависит выбор способа обзора пространства.
Уровень боковых лепестков снижает мощность, скрытность, электромагнитную совместимость, помехозащищенность. Ширина ДН влияет на точность измерения координат и на разрешающую способность.
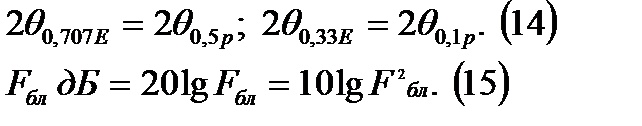
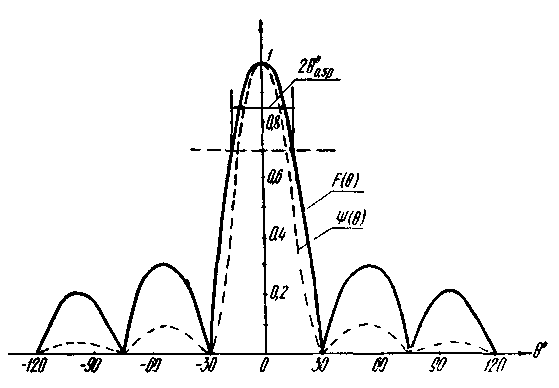
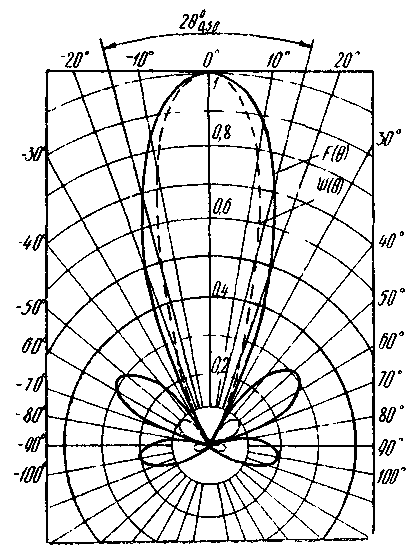
Ниже изображены ДН в прямоугольной системе координат, в полярной системе координат и реже отображают ДН картографическим способом.

Фазовая ДН- называют зависимость начальной фазы поля от пространственных углов 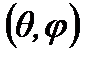 при неизменных условиях наблюдения(фиксированного расстояния от начала координат) и возбуждения. Для характеристики фазы удобно рассматривать эквифазные поверхности которые тесно связаны с фазовой ДН. Эквифазная поверхность(фронт волны) представляет собой поверхность в пространстве во всех точках которой в данный момент времени фаза одинакова.(16) уравнение эквифазной поверхности,
при неизменных условиях наблюдения(фиксированного расстояния от начала координат) и возбуждения. Для характеристики фазы удобно рассматривать эквифазные поверхности которые тесно связаны с фазовой ДН. Эквифазная поверхность(фронт волны) представляет собой поверхность в пространстве во всех точках которой в данный момент времени фаза одинакова.(16) уравнение эквифазной поверхности, 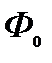 начальная фаза тока,
начальная фаза тока, 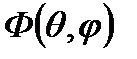 фазовая ДН.
фазовая ДН.
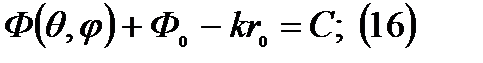
Решаем относительно 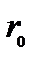 получаем уравнение сферы.
получаем уравнение сферы.
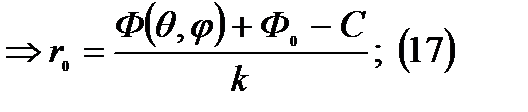
В отличии от амплитудной ДН, фазовая ДН зависит от положения начала координат на антенне. Если сместить начало координат на 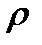 ,то в новой фазовая ДН будет определяться:
,то в новой фазовая ДН будет определяться:
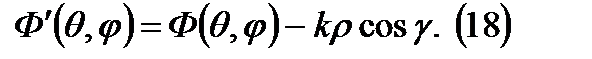
Если можно найти такое положение начала координат в антенне, где фазовая ДН=const или меняется скачком от одного лепестка к другому, то говорят что начало координат совпадает НК совпадает с фазовым центром антенны. В этом случае фронт волны представляет собой часть сферы хотя бы в пределах ДН, следовательно, антенна имеет фазовый центр. Также, Если в пределах ДН получаем сферическую волну и фаза там либо постоянна либо меняется скачком на п при переходе от одного главного луча на другой, то имеется фиктивный фазовый центр.
Облучатель помещаем в фазовый центр, если фазового центра нет то можно совместить облучатель с фокусом параболоида, тем самым обеспечить в пределах ДН сферическую волну, эту точку принимаю за фиктивный(условный) фазовый цент антенны.
Коэффициент усиления.
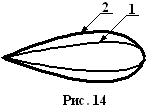 КУ характеризует степень выигрыша антенны с учетом потерь в ней. Подводимые мощности одинаковы, ДН разные. У 1й антенны потери больше чем во второй. Потери характеризуются КПД.
КУ характеризует степень выигрыша антенны с учетом потерь в ней. Подводимые мощности одинаковы, ДН разные. У 1й антенны потери больше чем во второй. Потери характеризуются КПД. 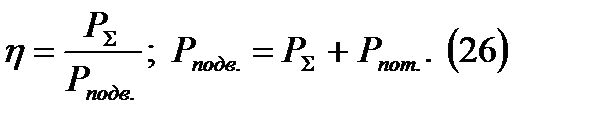
КУ показывает во сколько раз мощность подводимая к изотропной антенне не имеющей потерь должна быть мощности подводимой к рассматриваемой антенне при условии равенства полей возбуждаемых этой антенной в направлении углов 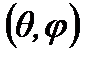 .
.
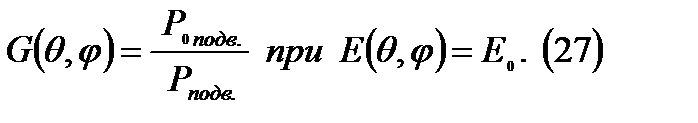
Домножим числитель и знаменатель на 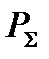 :
: 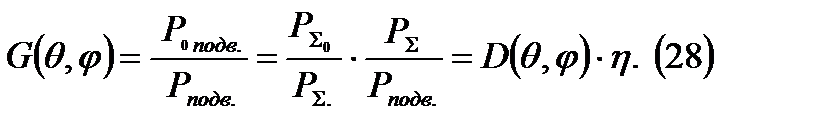
Замечание: Для УКВ диапазона 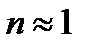 , следовательно
, следовательно 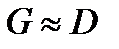 .
.
Поляризационная ДН. Величины 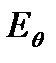 и
и 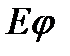 напряженность электрического поля в азимутальной и угломестной плоскостях имеют различные амплитуды и как правило сдвинуты по фазе. Поле антенны будет поляризовано элептически. Рассмотрим поляризационный эллипс.
напряженность электрического поля в азимутальной и угломестной плоскостях имеют различные амплитуды и как правило сдвинуты по фазе. Поле антенны будет поляризовано элептически. Рассмотрим поляризационный эллипс.
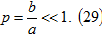
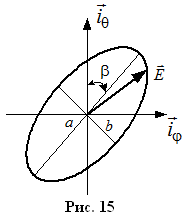 Вводится параметр называем коэффициентом поляризации.
Вводится параметр называем коэффициентом поляризации.
(меньше либо равен)
Характеризуется углом наклона большей оси эллипса и направлением вращения вектора Е. При переходе из одной точки в другую, параметры поляризационного эллипса меняются.
Зависимость коэффициента поляризации поляризационного эллипса от пространственных углов 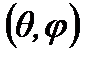 называют поляризационной ДН. В общем случае у нас линейная поляризация, на приемном конце нужно ставить антенну с такой же поляризацией.
называют поляризационной ДН. В общем случае у нас линейная поляризация, на приемном конце нужно ставить антенну с такой же поляризацией.
Частотный диапазон.
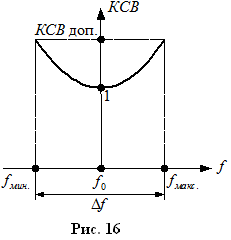 Для обеспечения режима бегущих волн регистрируем коэффициент стоячих волн, на центральной частоте он должен быть равен 1. КСВ=1.2 влево и вправо. (Допускается для наземных станций КСВ=1.15, воздушный КСВ=1.2) Зафиксировав данные значения, получили диапазон частот в котором антенна не теряет своих качеств.
Для обеспечения режима бегущих волн регистрируем коэффициент стоячих волн, на центральной частоте он должен быть равен 1. КСВ=1.2 влево и вправо. (Допускается для наземных станций КСВ=1.15, воздушный КСВ=1.2) Зафиксировав данные значения, получили диапазон частот в котором антенна не теряет своих качеств.
Интервал частот, в котором заданные параметры антенны не выходят из заданных границ, называют рабочим диапазон частот антенны, те полосой пропускания.
Рабочий диапазон определяют по изменению входного сопротивления антенны. В режиме бегущих волн выходное сопротивление передатчика согласовано с длинной линией и входным сопротивлением антенны(на передачу). Сопротивление антенны должно быть согласовано с волновым сопротивлением тракта передачи и входным сопротивлением приемника(на прием). Если есть рассогласование, но в пределах указанного, это покажет и сопротивление(должно быть чисто активным, и = волновому). Антенна выполняет роль пространственного фильтра(ДН), частотного фильтра, поляризационного фильтра.
Ширина полосы пропускания:
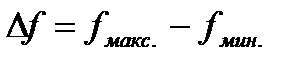
Вводится коэффициент перекрытия по частоте:
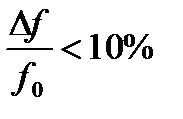 - узкополосная;
- узкополосная; 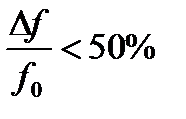 - широкополосная;
- широкополосная;
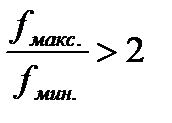 диапазонная. Вводится коэффициент перекрытия диапазона.
диапазонная. Вводится коэффициент перекрытия диапазона.
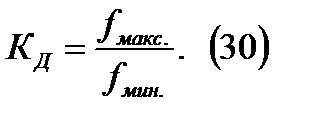 ,
, 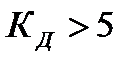 частотно независимые антенны(логопериодические антенны).
частотно независимые антенны(логопериодические антенны).
Допустимая величина излучаемой мощности. При напряженности поля более 30кВ/см вблизи антенны будет диэлектрический пробой.: Предельно допустимая определяется из E<30кВ/см, рабочую мощность антенны выбирают как правило в 2-3 раза меньше чем предельно допустимая. Величина предельно допустимой мощности излучения уточняется экспериментально.
Антенны, КИП, КНД, КУ, КПД.
Мощность в нагрузке:
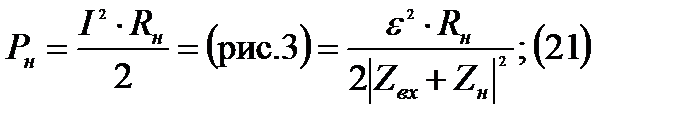 (правая часть из (4))
(правая часть из (4))
Максимальная мощность будет в том случае когда 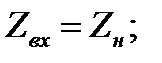
Мощность нагрузки согласованной: 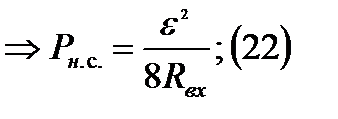
Рассмотрим отношение: 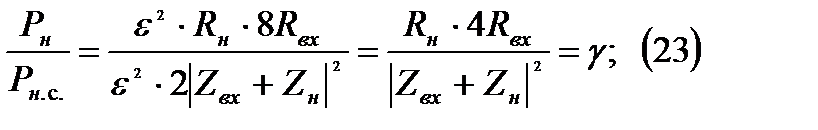
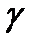 - коэффициент согласования, характеризует степень согласования антенны с нагрузкой. Далее преобразуем данное выражение:
- коэффициент согласования, характеризует степень согласования антенны с нагрузкой. Далее преобразуем данное выражение: 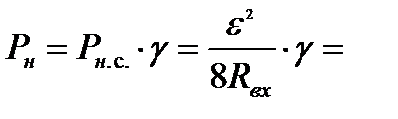 раскроем эдс из(15)
раскроем эдс из(15)
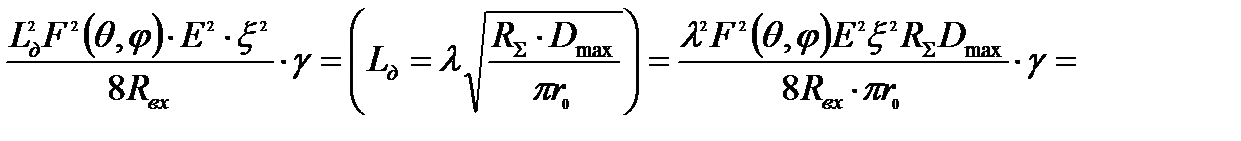 выделим отношение
выделим отношение 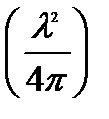
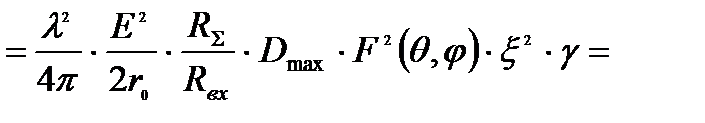 где
где 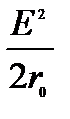 =S(плотность потока мощности),
=S(плотность потока мощности),
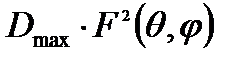 - текущий КНД.
- текущий КНД.
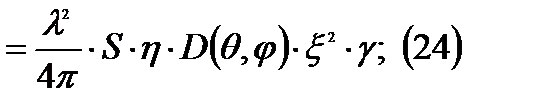
Полагаем что: 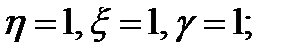
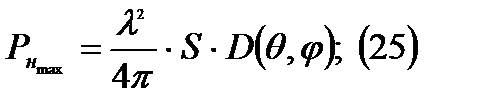 где
где 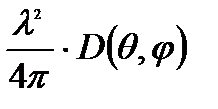 =
= 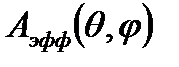 , тогда
, тогда 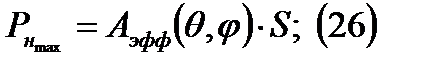
Соответственно:
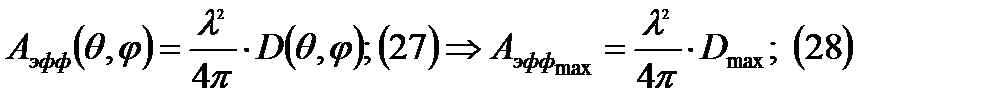
Т.к для УКВ диапазона 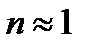 то:
то:
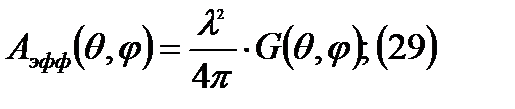
Здесь же применяется коэффициент использования поверхности.
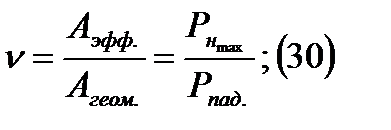 Показывает долю мощности, которую антенна извлекает из мощности падающей волны и передает в нагрузку, обычно он лежит в предела от 0,2 до 0,8.
Показывает долю мощности, которую антенна извлекает из мощности падающей волны и передает в нагрузку, обычно он лежит в предела от 0,2 до 0,8.
Понятие о дискретной системе излучателей. Поле системы излучателей. Теорема перемножения диаграммы направленности антенны (ДНА).
Пусть имеется некоторая дискретная система (набор дискретных излучателей) расположенных произвольным образом в пространстве. Определить поле в точке Р.
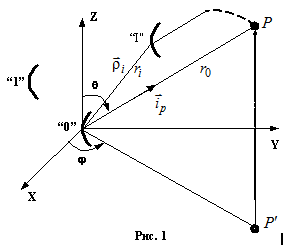 В законы электродинамики все параметры входят в первой степени, значит они линейны, следовательно, принцип суперпозиции применим. Разобьем антенну на элементарные излучатели, тогда поле в точке Р.
В законы электродинамики все параметры входят в первой степени, значит они линейны, следовательно, принцип суперпозиции применим. Разобьем антенну на элементарные излучатели, тогда поле в точке Р.
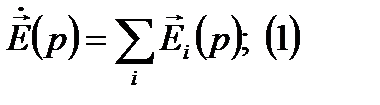
Поле центрального излучателя:
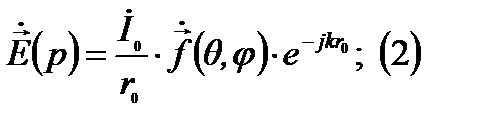
Соответственно поле i-го излучателя:
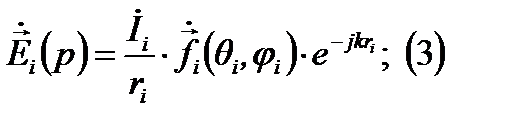
Комплексная векторная ДН определяется:
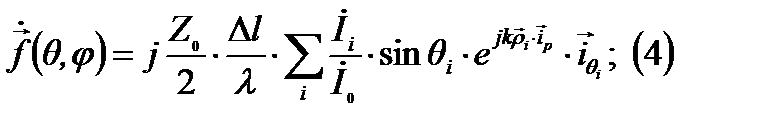
Т.к. источники идентичны то и их ДН идентичны:
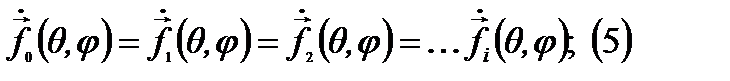
Т.о. поле в точке наблюдения можно записать:
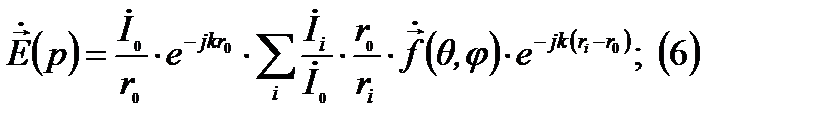 А так как поле мы рассматриваем в дальней зоне, то
А так как поле мы рассматриваем в дальней зоне, то 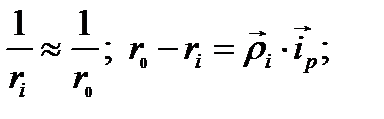 (справа из прошлой темы).
(справа из прошлой темы). 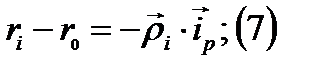
Проанализируем выражение(6) преобразованное с учетом (5) и (7):
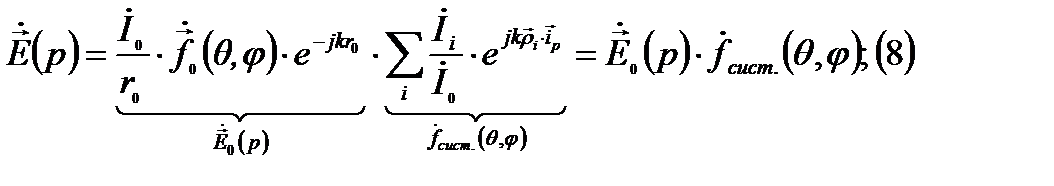
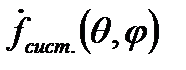 -множитель системы.
-множитель системы.
Правило перемножения диаграмм(правило Бонч-Бруевича)
Проведем математические преобразования:
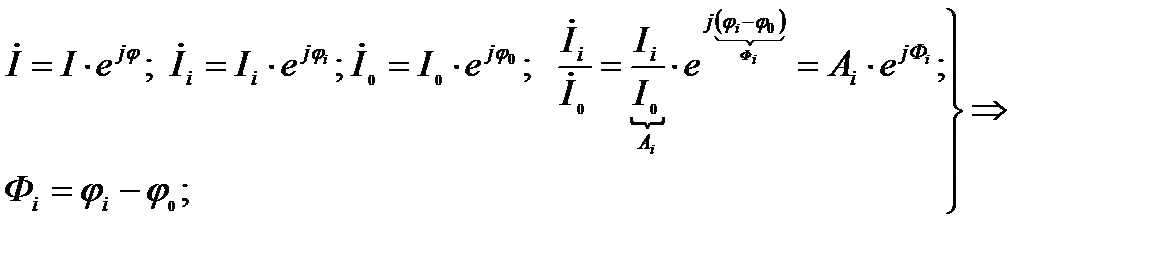 (8)
(8) 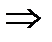
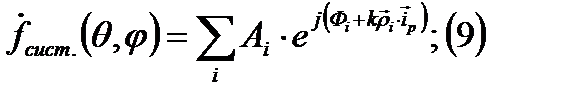
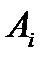 - амплитудное распределения в системе токов или полей.
- амплитудное распределения в системе токов или полей. 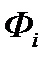 -фазовое распределение токов или полей.
-фазовое распределение токов или полей.
Мы можем записать:
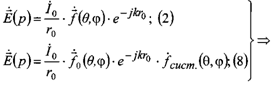
Соответственно:
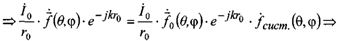
Отсюда и вытекает правило перемножения диаграмм. Если нам необходимо определить ДН системы дискретных излучателей мы должны взять ДН центрального излучателя и умножить на множитель системы. Условия применения: идентичные излучатели, одинаково ориентированы, одна поляризация.
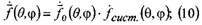
Физический смысл множителя системы - состоит в том, что он описывает пространственную, интерференционную картину излучения(комплексную ДН), системы изотропных излучателей с тем же амплитудно-фазовым распределением что и в антенне.
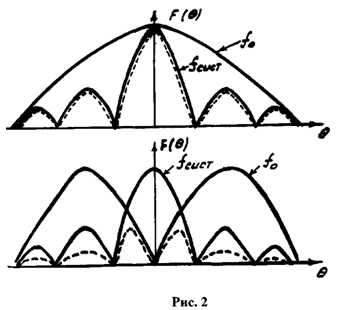 Графическая интерпретация правила перемножения диаграмм.
Графическая интерпретация правила перемножения диаграмм.
Результирующая ДН изображена пунктиром.
В основном ДН определяет множитель системы.
При перемножении не должно быть чтобы макс множителя системы совпадал, с мин ДН центрального излучения.
Анализ множителя линейной дискретной системы. Направление главных максимумов и ширина ДН. Условие единственности главного максимума. Направление нулевого излучения и боковые лепестки. Коэффициент направленного действия.
Рис 4
Запитка синфазная, отличается только фазовый множитель. Т.к. электромагнитную энергию лучше передавать одним лепестком (лучше помехозащищенность и скрытность, электромагнитная совместимость). Считаем что антенна является синфазной(каждый элемент запитан в одной фазе). Получим условие единственности главного лепестка в виде:
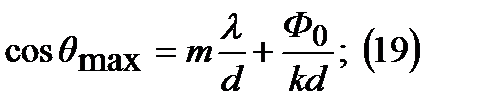
Замечание:
Максимум излучения идет по нормали(так как элементарный вибратор). Если учитывать угол от оси решетки к нормали то будет cos если наоборот то sin.
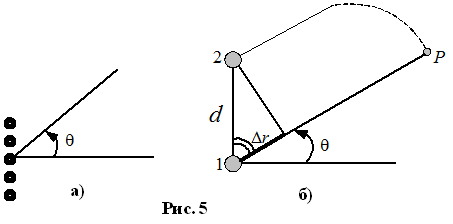 Анализируем поле в точке P. Разность хода будет:
Анализируем поле в точке P. Разность хода будет:
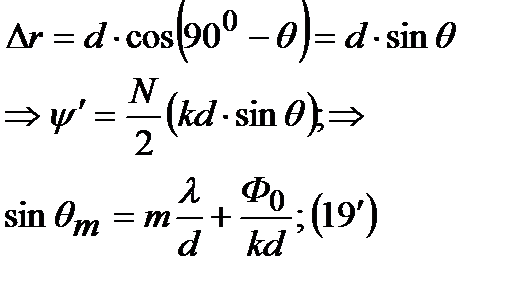
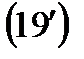 Условие единственности главного лепестка.
Условие единственности главного лепестка.
Рассмотри размеры рабочей области, в общем случае: 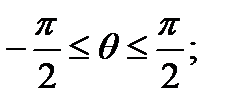 (оласть реальных урлов) должен лежать в таких пределах;
(оласть реальных урлов) должен лежать в таких пределах; 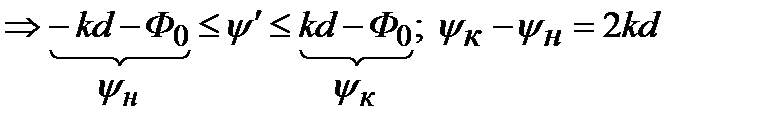 (н-начала, к-конца) Отсюда:
(н-начала, к-конца) Отсюда:
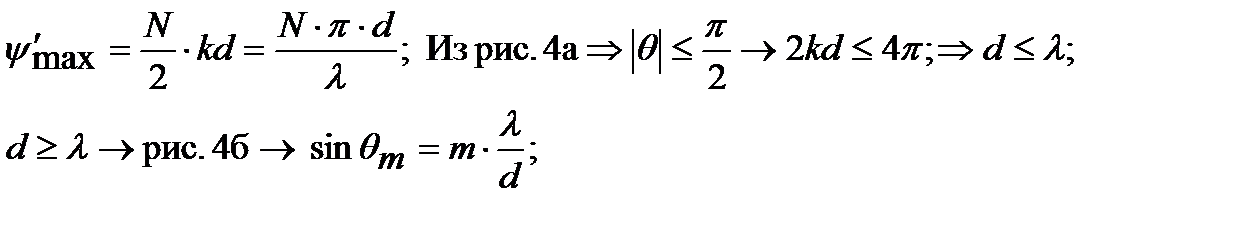
Рассмотри рисунок(тоже что и рис 4), но рабочая зона смещена из за несинфазной запитки.
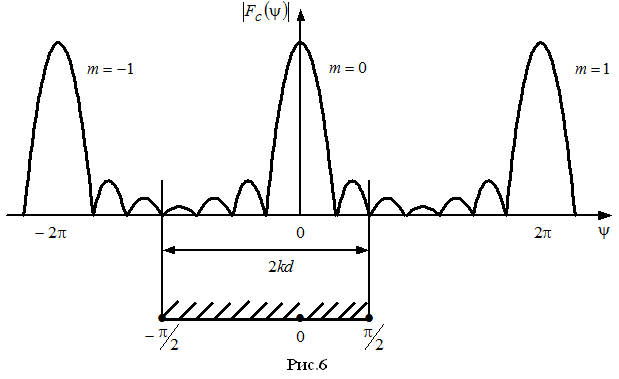
Меняя фазовое распределение обеспечивается сканирование лучом ДН в пространстве. При сканировании ДН область рабочих углов смещается, а в области реальных углов ДН смещается. Не нарушим ли мы условие единственности лепестка, и что мы должны учитывать при вращении ДН в пространстве. Будем исходить из условия ед гл лепестка
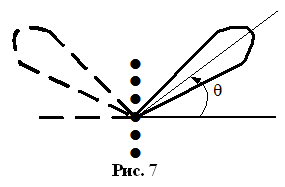
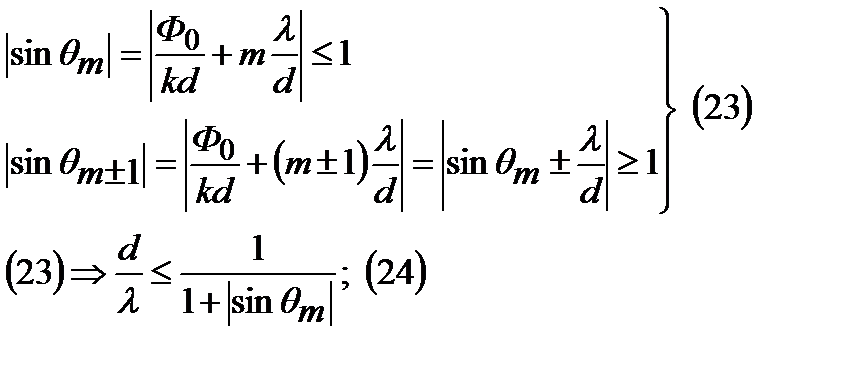
Учитываем излучатели: 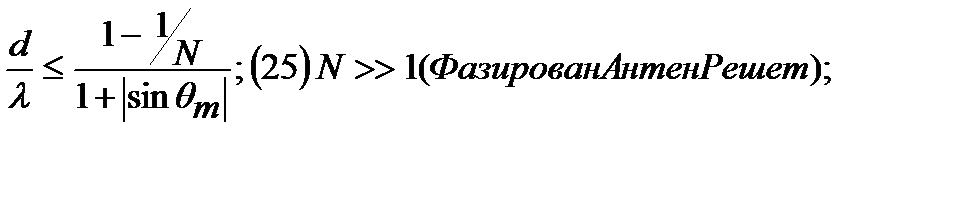
Соответственно условие ед. гл. лепестка при сканировании: 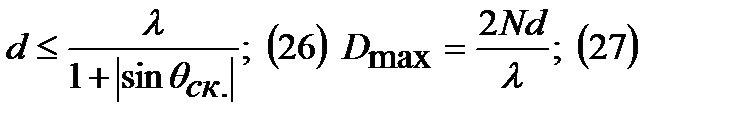
Пример: Построим множитель системы 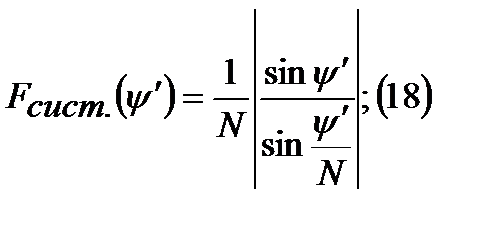 . Построим числитель: Функция периодическая, а так N=4, то построим 4п, амплитуда соответственно
. Построим числитель: Функция периодическая, а так N=4, то построим 4п, амплитуда соответственно 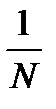 . График ниже знаменателя синусоида расширенная в 4 раза. Дальше третий график числитель разделим на знаменатель ,неопределенность 0/0 дает максимум. Затем считаем вещественный угол. Далее рисуем максимум главного луча, и боковые лепестки. Самый нижний рисунок при не синфазной запитке.
. График ниже знаменателя синусоида расширенная в 4 раза. Дальше третий график числитель разделим на знаменатель ,неопределенность 0/0 дает максимум. Затем считаем вещественный угол. Далее рисуем максимум главного луча, и боковые лепестки. Самый нижний рисунок при не синфазной запитке.

Круглый излучающий раскрыв.
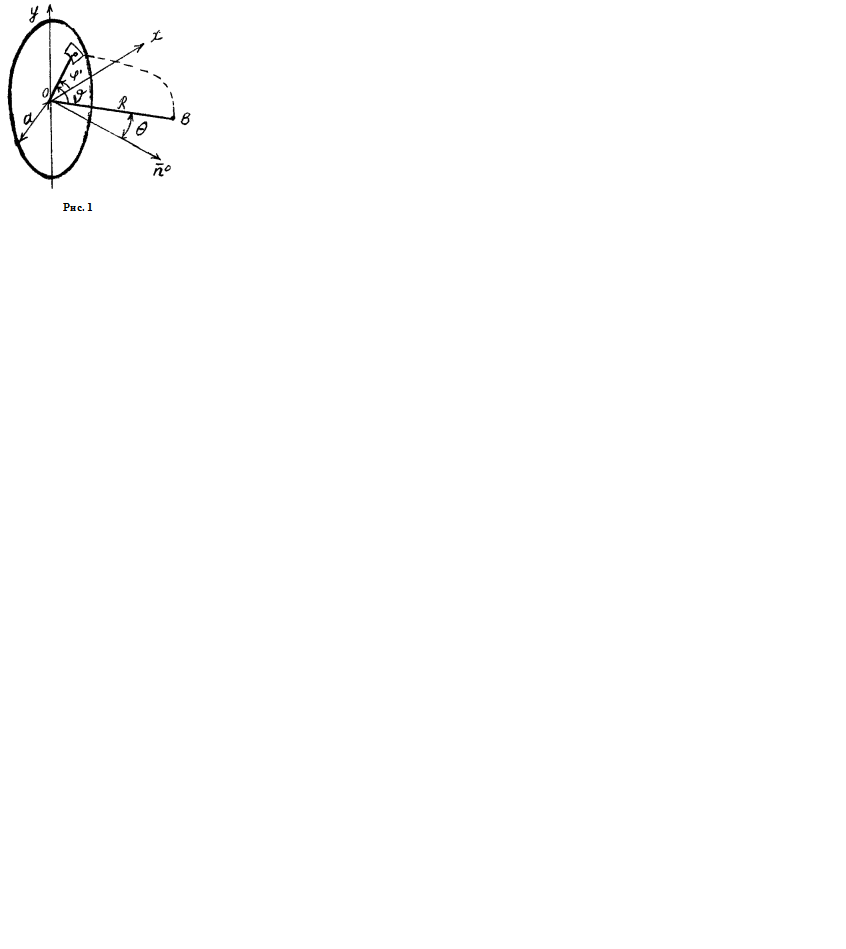 Рассмотрим круглый излучающий раскрыв. Поместим
Рассмотрим круглый излучающий раскрыв. Поместим
начало координат в центр раскрыва и выразим амплитудно-фазовое распределение через полярные координаты раскрыва и подставим их в выражение (3).
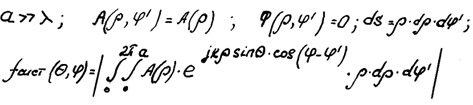
Наиболее часто используются синфазные раскрывы с амплитудным распределением, не зависящим от радиуса  также введем некоторые обозначения, получим:
также введем некоторые обозначения, получим:
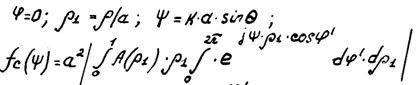
Используя представление для функции Бесселя нулевого порядка:
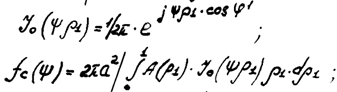
Как это следует из физических соображений, множитель системы от 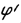 не зависит, является вещественной функцией. Последнее означает, что раскрыв излучает сферическую волну. Фазовый центр находится в центре антенны. В случае равномерного амплитудного распределения:
не зависит, является вещественной функцией. Последнее означает, что раскрыв излучает сферическую волну. Фазовый центр находится в центре антенны. В случае равномерного амплитудного распределения:
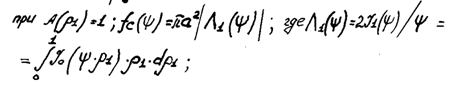
При: 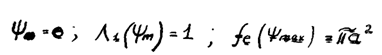
Нормированная ДН:
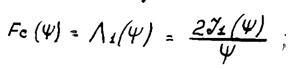
Ширина ДН, уровень боковых лепестков, КНД, и коэффициент использования поверхности:
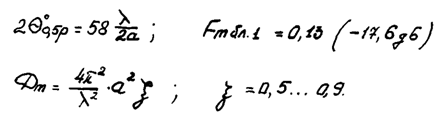
Таким образом, видно, что при переходе от прямоугольно раскрыва к круглому приводит снижению уровня боковых лепестков и расширению главного лепестка.
Замечание:
Максимум излучения идет ортогонально оси вибратора, вдоль своей оси вибратор не излучает. Полученный выше результат можно найти другим путем:
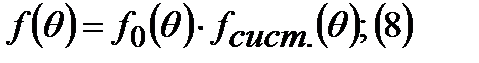 ДН элементарно излучатели известна:
ДН элементарно излучатели известна: 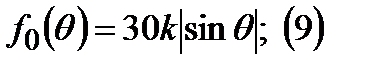
Получим множитель системы:
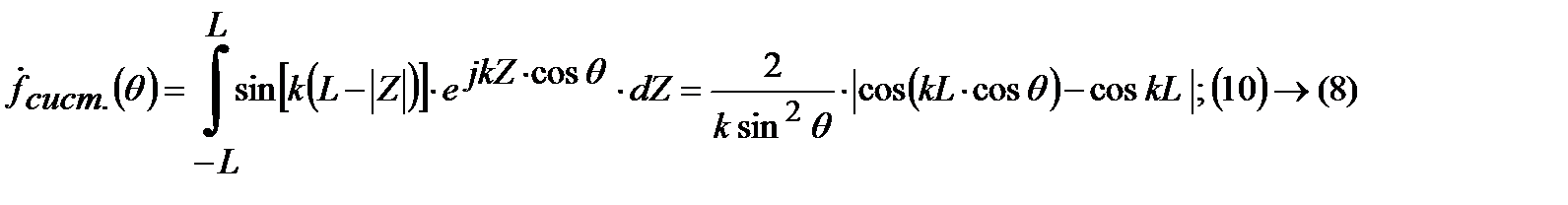
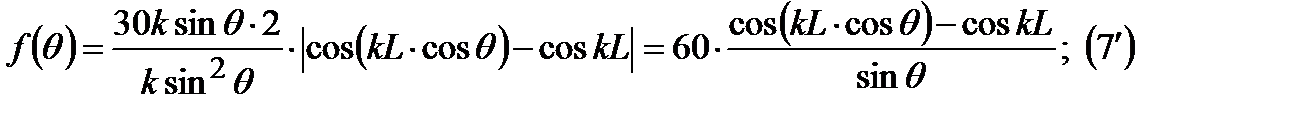
Получим нормированную ДН:
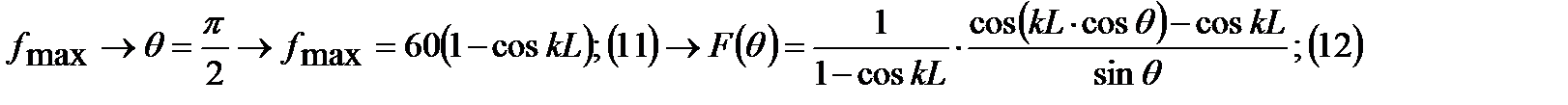
Т.к. мы рассматриваем полуволновый вибратор:
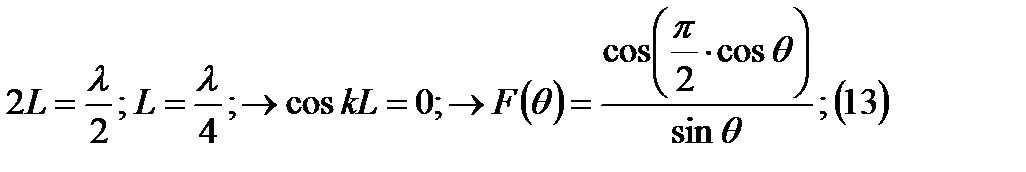
А если отсчет угла будет вестись от нормали к оси то:
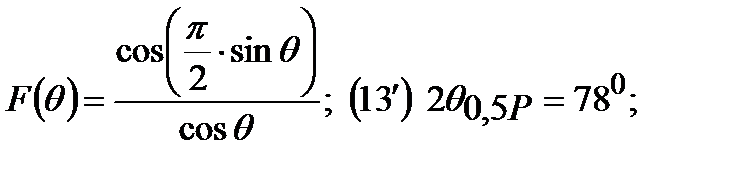
Вид ДН в зависимости от отношения L к длине волны:
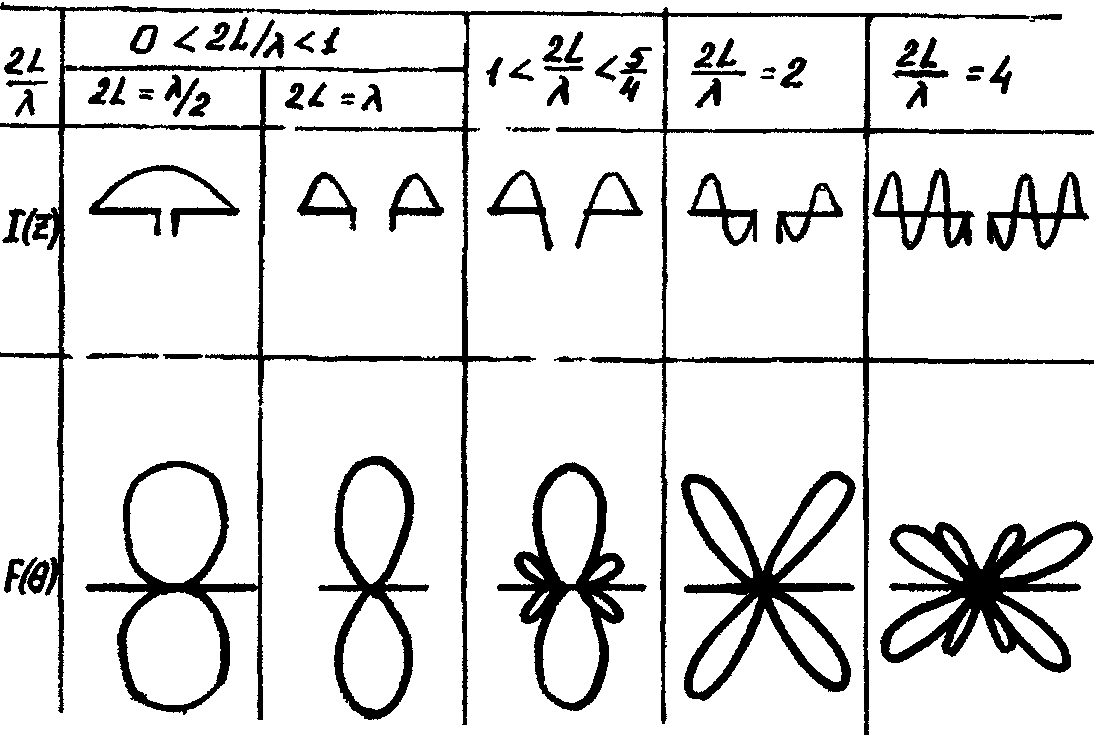
При увеличении длинны антенны, ДН сужается, но растет уровень боковых лепестков.
Сопротивление излучения симметричного вибратора затабулирована:
 КНД:
КНД:
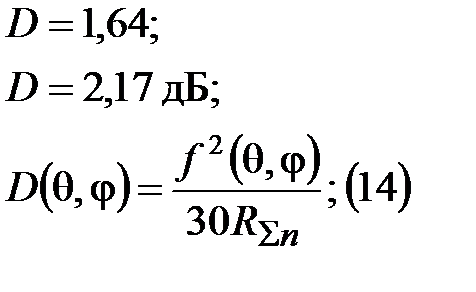
Компенсационный способ.
К симметричному полуволновому вибратору подключается короткозамкнутый отрезок длинной линии(стакан). Реактивное сопротивление на волнах близких к резонансной очень великой, что равносильно его отключению. На других волнах реактивное сопротивление вибратора и компенсатора имеют противоположные знаки поэтом происходи их компенсация.
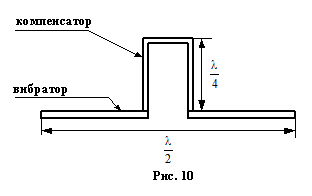
4)Комбинированный способ.
Реализован в вибраторах Брауде.
 1 способ увеличение площади вибратора
1 способ увеличение площади вибратора
2.Компенсационный способ.
E - cекториальный рупор.
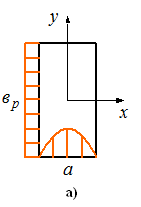
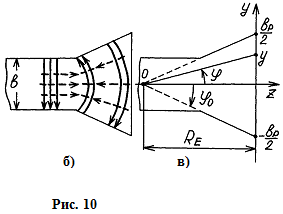
Плавно расширяется узкая стенка волновода.
АФР:
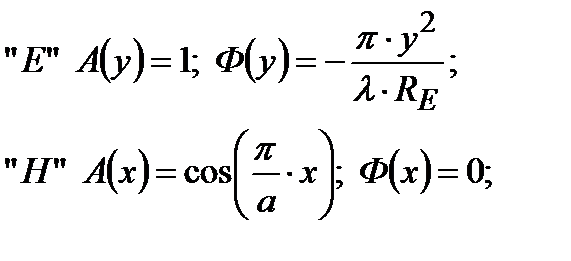
Множитель системы:
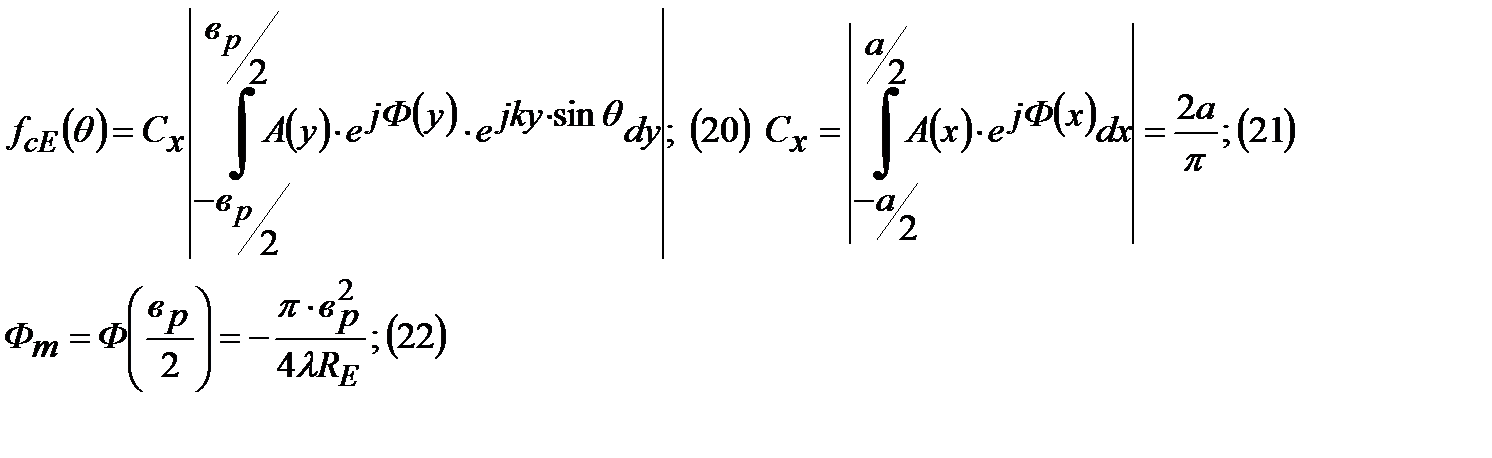
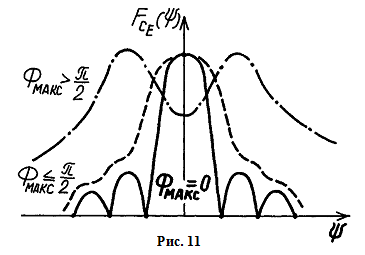 ДН:
ДН:
Фазовое распределение сказывается сильнее чем в H- секториальном рупоре.
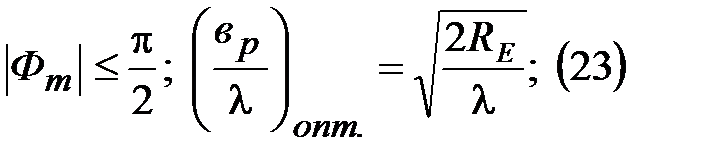
Результат расчетов параметров E- Зависимость КНД от отношения 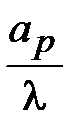 .
.
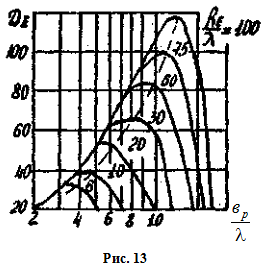 секторального рупора. (веерная ДН)
секторального рупора. (веерная ДН)
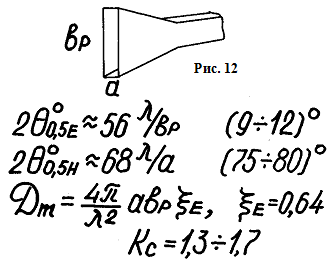
Для того чтобы улучшить согласование с окружающим пространством, сформировать игольчатую ДН используют рупорные антенны.
Пирамидальный рупор
Пирамидальным рупором называют такой рупор, у которого увеличиваются размеры в обеих плоскостях
Пирамидальный рупор можно рассматривать как сочетание Е и Н секториальных рупоров. Следует различать остроконечный рупор у которого продолжение ребер пересекаются в одной точке то есть RE=RH=R и клиновидный рупор у которого RE ≠RH
Приблизительно можно считать, что структура поля в пирамидальном рупоре примерно такая же, как и в исходном волноводе. В остроконечном рупоре фронт волны сферический, в клиновидном поверхность двойной кривизны. При удалении от вершины фазовая скорость волны в рупоре стремится к скорости света. Волна становится поперечно , а волновое сопротивления стремится к волновому сопротивлению свободного пространства.
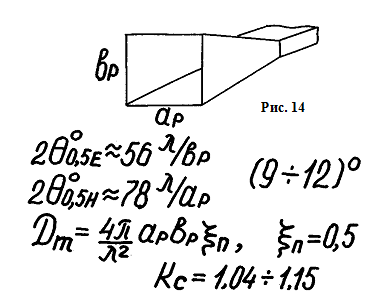
КНД считают используя ряд практических формул:
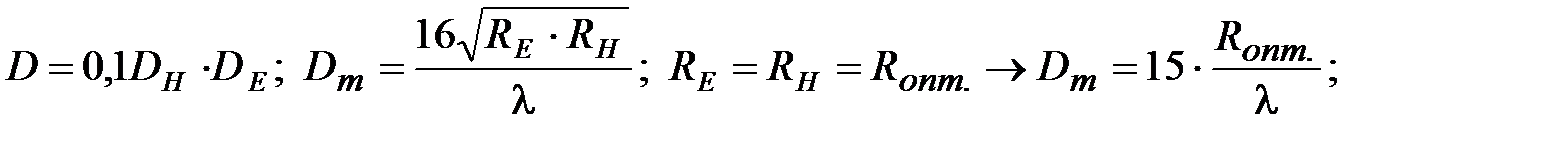
Вид ДН: 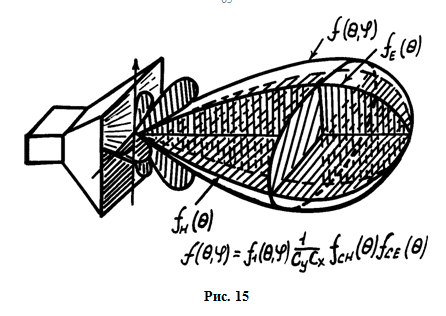
Конический рупор.
Довольно активно в системах спутниковой связи используют конический рупор
Конический рупор – это рупор с расширяющимся круглым поперечным сечением.
Для конического рупора, возбуждаемого круглым волноводом с волной Н11 можно следующие выводы. Амдитудное распределение в раскрыве примерно такое же как и у круглого волновода, а фаза изменяется по квадратичному закону.
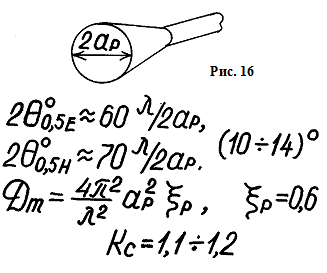
Рупорные антенны можно использовать и как самостоятельные антенны и как облучатели более сложных антенн например зеркальных антенн.
Сканирование ДН.
В антенных решетках применяются 2 основных способа качания электрического луча: фазовый (изменение фазы с помощью фазовращателей) и частотный (изменение частоты источника питания). Цель – добиться линейного фазового распределения. Иногда выделяют амплитудный метод качания, который реализуется путем коммутации входов в многолучевых антенных решетках, или линзах Люниберга. Временной способ реализуется в широкополосных АР с помощью линии задержки.
Фазовый способ:
Фазовое управление наиболее часто используется. От излучателя к излучателю фаза меняется. (3) множитель дискретной системы излучателей. (4) условие единственности главного лепестка. Скорость нарастания линейно фазового распределения и характеризует скорость отклонения ДН. 
Частотный способ
При изменении несущей частоты генератора направление главного максимума перемещается в соответсвии с выражением (4). Это выражение характеризует эффективность и называется углочастотной зависимостью
Частотный метод, для изменения направления ДН, используется изменение частоты. Соответственно радиопередающее устройство должно иметь довольно большой диапазон перестройки частот. Также синхронно передатчику должен переключатся и приемник.
Углочастотная зависимость характеризует отклонение луча в градусах на 1 % отклонения частоты. Современные СВЧ генераторы допускают перестройку по частоте в пределах нескольких процентов от несущей. Для того, чтобы при таком изменении частоты осуществить перемещение луча в достаточно широком секторе величина qдолжна быть порядка 10° на %, иногда и больше.
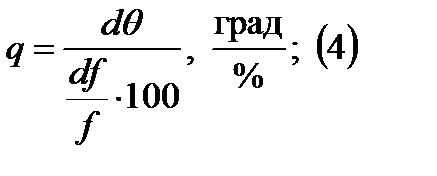
Последовательная схема, передатчик подключен к волноводной системе. Эквидистантное расстояние(расстояние между) излучателями d.
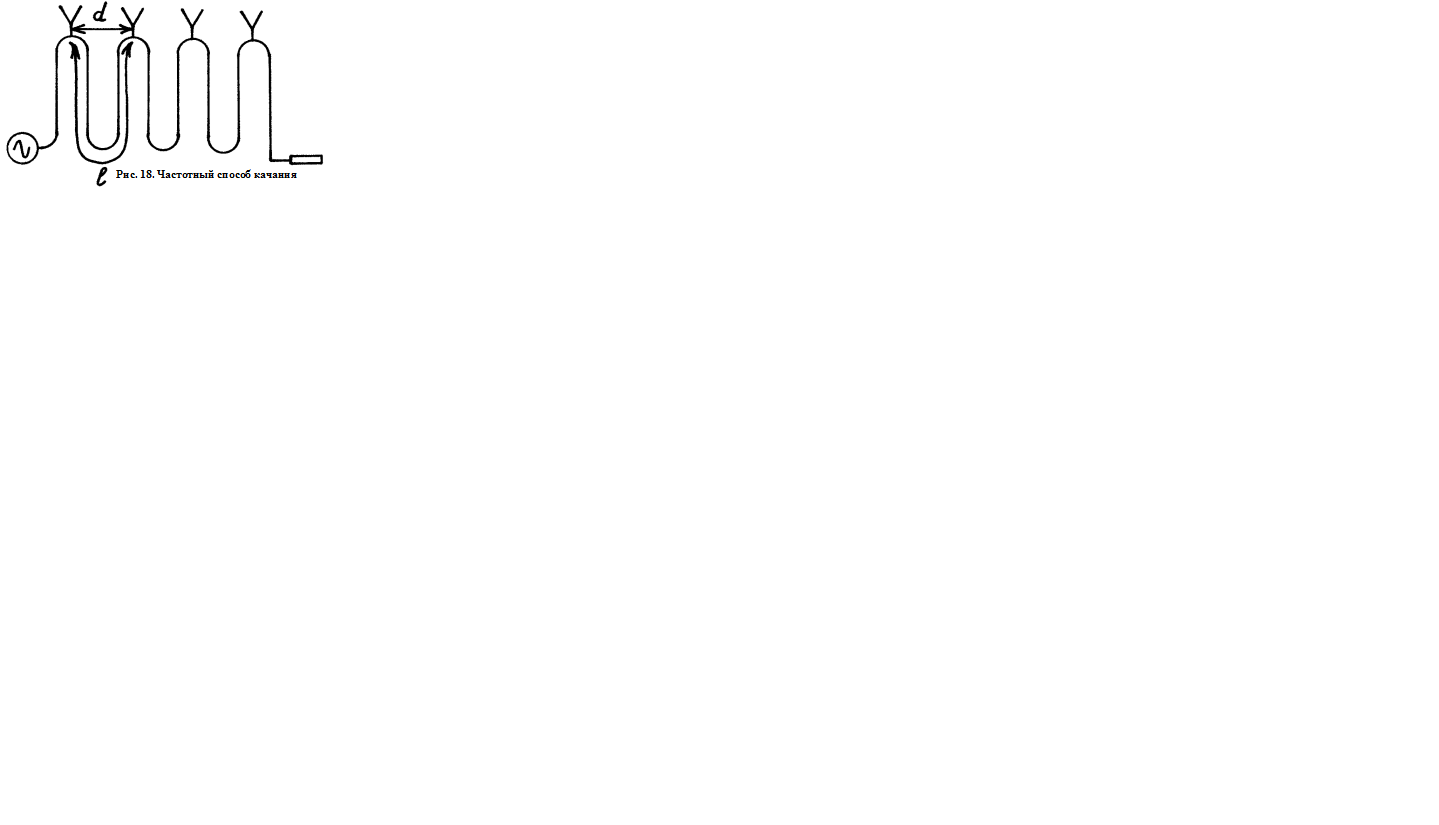
Выясним от чего зависит фаза. Продифференцируем выражение (4).
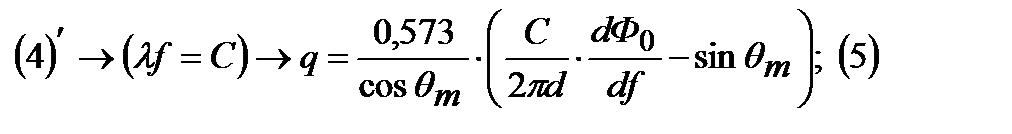
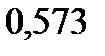 -возник при переходе от радиан к градусам. Анализ этого выражения показывает, что увеличить мы можем увеличением сомножителя. Более резкая смена фаз при заданном изменению частоты приводит к большему изменению величины q и большему отклонению луча.
-возник при переходе от радиан к градусам. Анализ этого выражения показывает, что увеличить мы можем увеличением сомножителя. Более резкая смена фаз при заданном изменению частоты приводит к большему изменению величины q и большему отклонению луча.
Т.к.физический смысл производной это скорость, второй сомножитель в скобках, это скорость изменения фазы при изменении частоты.
Фазу можно записать(как в кольцевом мосте):
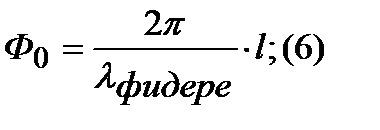
Продифференцируем (6):
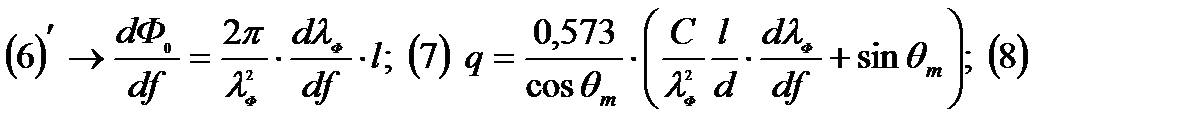 - выражение (5) преобразуется в (8).
- выражение (5) преобразуется в (8).
Из выражения (8) можно выделить два пути увеличения углочастотной зависимости: использование фидеров с резко выраженной дисперсией (зависимостью параметров среды от частоты) - 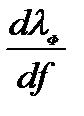 ; увеличение отношение Lк d, т.е. геометрического замедления в системе.
; увеличение отношение Lк d, т.е. геометрического замедления в системе.
Таким образом изменяя 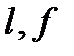 мы можем изменять фазу, т.е имеется возможность частотного управление ДН ФАР.
мы можем изменять фазу, т.е имеется возможность частотного управление ДН ФАР.
Параллельный способ

Пример с изменением длины:
Специальные типы антенн.
Для того чтобы излучить и принять сигнал с круговой поляризацией использую(самый простой вариант) турникетные антенны, которые представляют собой сочетание горизонтального и вертикального вибратора подключенных к одному передатчику по пути l1 и l2.
Условие круговой поляризации(набег фаз на 90 градусов осуществляется за счет разности l1-l2):
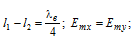
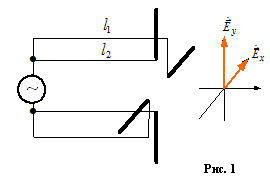
Алгоритм работы данной системы:
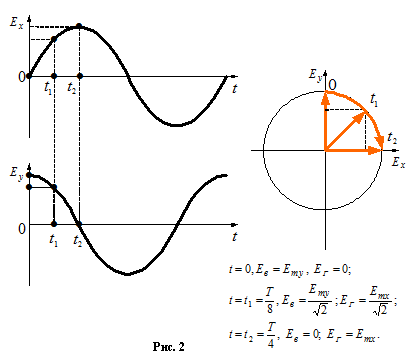
ДН данной турникетной антенны:
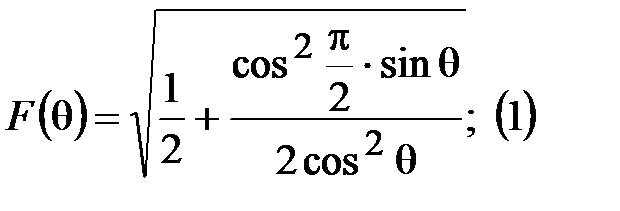
Вид ДН:

Ширина данной ДН большая, соответственно КНД небольшой. Для сужения ДН используется метод увеличения количества излучателей.

Чтобы сузить ДН в двух плоскостях используют многоэтажные турникетные антенны. Вертикальный вибратор схематично показан слева.

Спиральные антенны
Часто используются спиральные антенны. Направителями спиральных антенн являются отрезки волноводов.

В простейшем случае антенна выполняется из цилиндрической проволочной спирали, протяженностью несколько длин волн. Диаметр 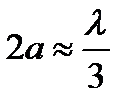 .
.
Определим амплитудное распределение. В этой антенне распространяются волны T типа.
В данном случае гибридные H и E волны их обозначают:
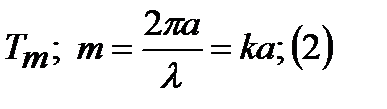 - характеризует число длин волн, укладывающихся на одном витке спирали. Обычно в спиральных антеннах возбуждаются волна типа T`1, которая обеспечивает режим осевого излучения.
- характеризует число длин волн, укладывающихся на одном витке спирали. Обычно в спиральных антеннах возбуждаются волна типа T`1, которая обеспечивает режим осевого излучения.
Распределение комплексных амплитуд тока:
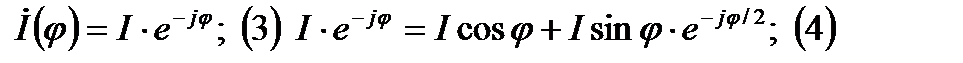
В спиральной антенне можно представить движение волны как суперпозицию двух стоячих волн (по закону косинуса и синуса), которые сдвинуты по фазе на π/2.
Фактически каждый виток спирали представляет собой 4 вибратора, которые попарно ориентированы вдоль взаимоперпендикулярнах осей и запитаны со сдвигом 90°.
В результате указанные вибраторы вдоль оси спирали возбуждают поле круговой поляризации. При отклонении точки наблюдения от оси спирали поле имеет эллиптическую поляризацию.

Если длинную линию свернуть в кольцо, мы получим тоже самое что и на рис. 7.


При достаточно большом числе витков ДН определяется множителем системы.
Если шаг намотки списали меньше длины волны:
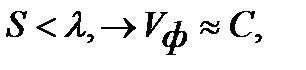 Токи в соседних виткахсинфазныт.е. замедление в данной системе мало. Распространяется слабозамедленная волна.
Токи в соседних виткахсинфазныт.е. замедление в данной системе мало. Распространяется слабозамедленная волна.
Каждый виток мы можем считать излучателем, тогда:
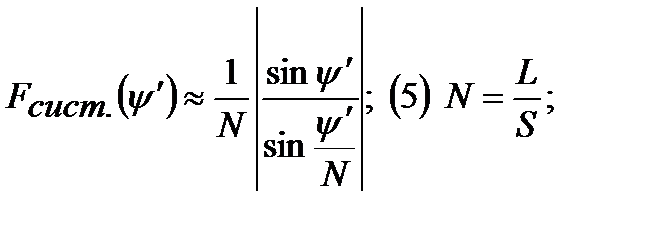
Обобщенный угол:
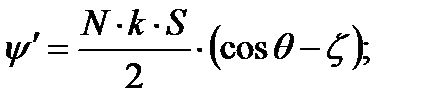 коэффициент замедления
коэффициент замедления 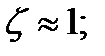 Спиральная антенна возбужденная волной Т1 представляет собой антенну бегущей волны с осевым излучением.
Спиральная антенна возбужденная волной Т1 представляет собой антенну бегущей волны с осевым излучением.
Диаметр отражателя(рефлектора):
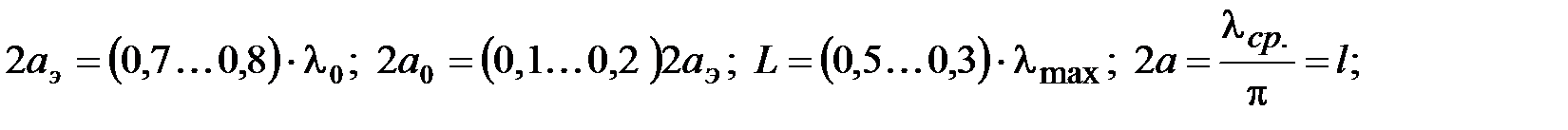 Зависимость ДН от отношения
Зависимость ДН от отношения 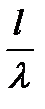

Как правило:
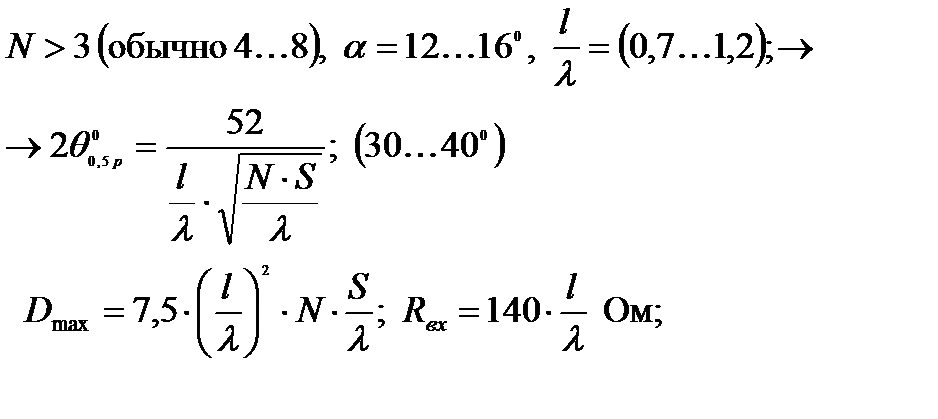
- Ширина ДН
- КНД
Кперектрытия по частоте =1,6…1,8.
Для сужения ДН используются решетки:
Рис. 11
Для того что антенна работала в большем диапазоне частот применяют антенны форм:

Рис. 12
Коэффициент перекрытия соответственно больше.
Кп (кон.) = 2…5, Кп (лог.) до 20.
Волноводная антенна.
Рупорная антенна с управляемой вращающейся поляризацией. В большей степени используется в качестве облучателей.

Состав:
1 - Питающий волновод;2- переходная секция; 3-фазирующая секция; 4 - пирамидальный рупор.
Питающий волновод 1 повернут относительно фазирующей секции 3 на угол близкий к 450, благодаря этому в переходной секции полем основной волны питающего волновода H10, возбуждаются электромагнитные волны других типов. Размеры широкой и узкой стенки фазирующей секции подбираются таким образом, что бы в ней могли распространяться два типа волн H10 иH01,аэти волны имеют взаимно перпендикулярные плоскости поляризации (ПЕРВОЕ УСЛОВИЕ СУЩЕСТВОВАНИЯ КРУГЛОПОЛЯРИЗОВАННЫХ ВОЛН). Подбирая угол 1 относительно 3, и размеры 3 мы добиваемся равенства амплитуд взаимно перпендикулярных составляющих поля (второе условие). Рассчитав размер L, можно получить сдвиг фазы между H10 иH01 на 900. Таким образом, мы выполнили два условия существования круговой поляризации:
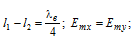
Получение фазового сдвига обусловлено тем, что фазовые скорости H10 иH01 различны:
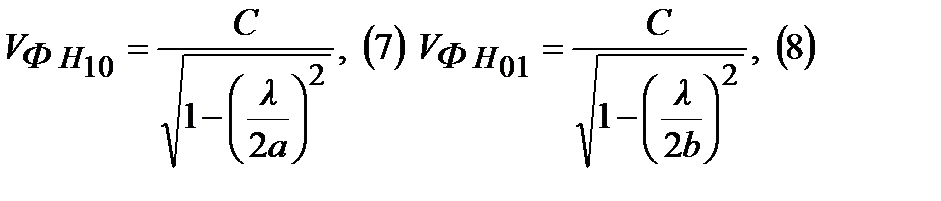
На выходе фазирующей секции с продольным размером L, разность фаз:
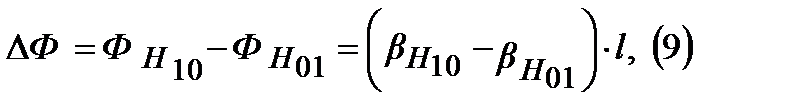
Где коэффициенты фазы:
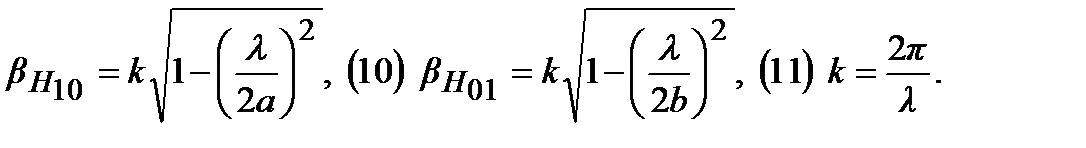
Подбирая L, получим разность фаз:
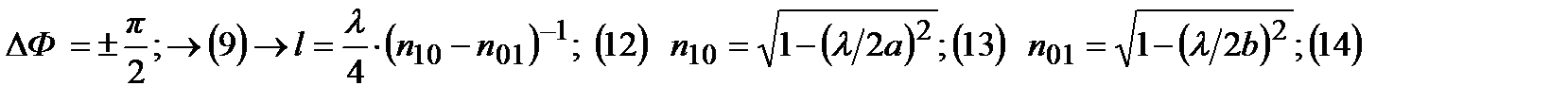 n-показатель преломления. Таким образом, данная антенна будет получать и принимать кругло поляризованные волны.
n-показатель преломления. Таким образом, данная антенна будет получать и принимать кругло поляризованные волны.
Рис. 2
Модуль отражения при горизонтальной поляризации близок к 1. Фаза изменяется, ей пренебречь нельзя и необходимо учитывать.
При вертикальной поляризации:
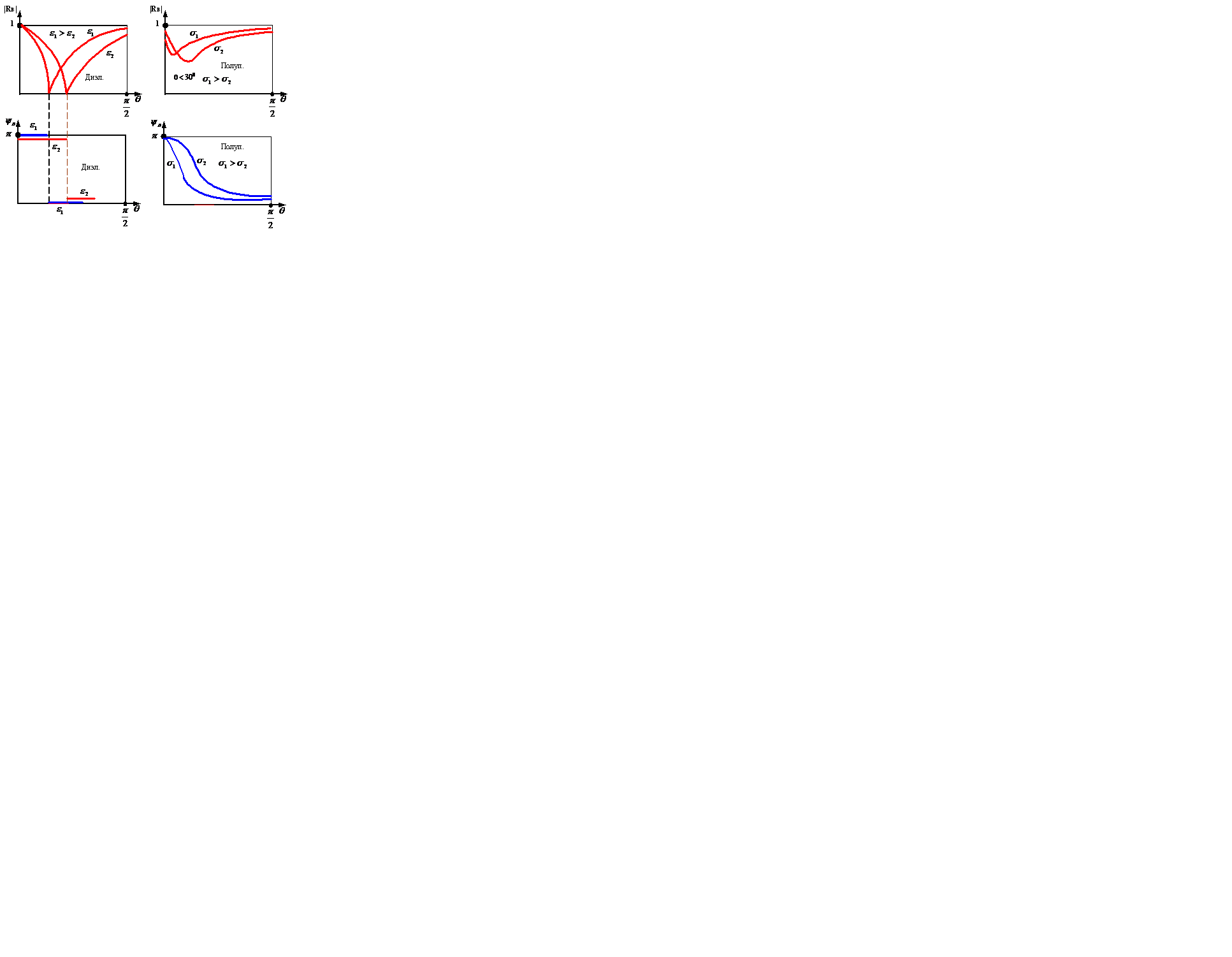
Модуль коэффициента отражения сильно изменяется(равен 0 при угле Брюстера). Для полупроводника при углах Брюстера наблюдается уменьшение модуля коэффициента отражения. Фаза изменяется скачком.
Учитывая эти данные запишем мощность прямой волны:

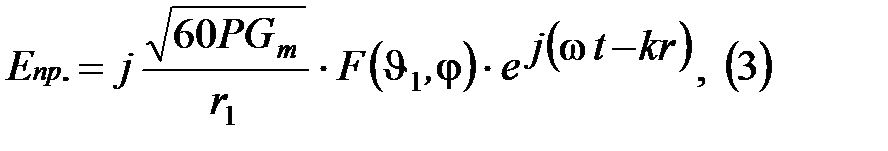
Для отраженной волны:
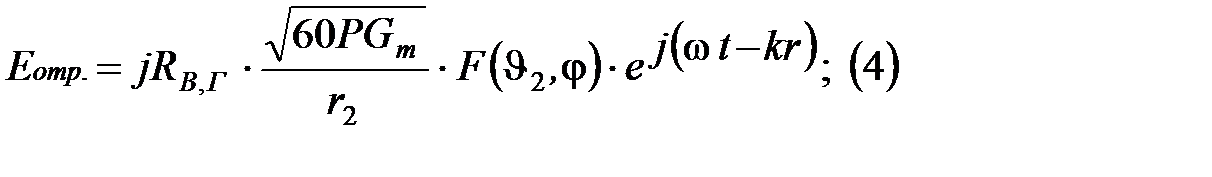
Предположим что ДН игольчатая:
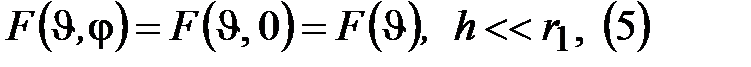 -условие дальней зоны.
-условие дальней зоны.

Дальней(Фраунгоферовой) зоной называют зону в которой лучи идущие от источника можно считать параллельными.
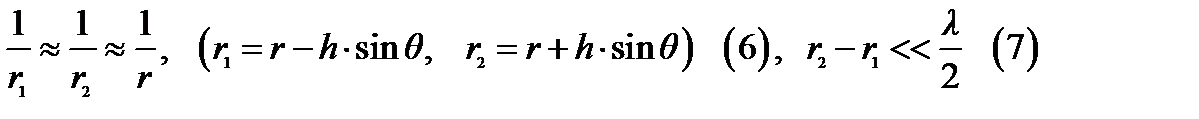
Критерий дальней зоны:
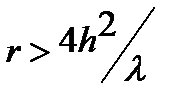
Т.к. диаграмма симметричная:
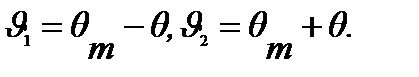
Учтем упрощения и запишем:
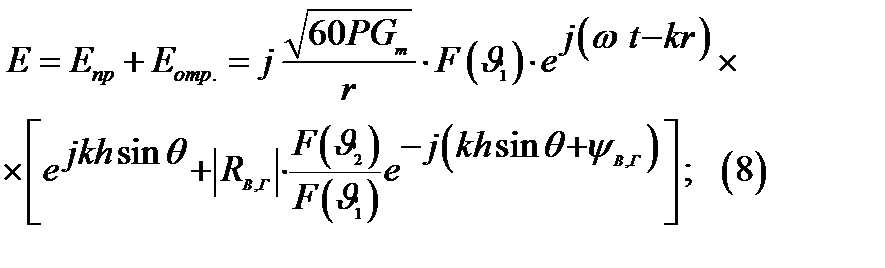
Выражение (8) представляет собой поле в свободном пространстве умноженному на множитель называемый, интерференционный множителем земли.
Модуль интерференционного множителя земли:
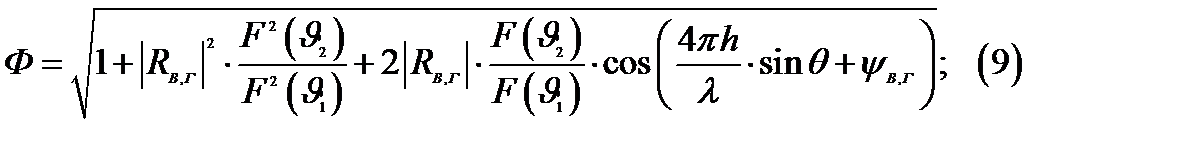
Отсюда поле в точке наблюдения:
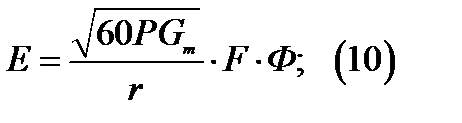
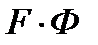 -характеристика направленности антенны, с учетом земной поверхности.
-характеристика направленности антенны, с учетом земной поверхности.
Интерференционный множитель земли характеризирует интерференционную картину лучей отраженных от земной поверхности.
Рассмотрим, как влияет интерференционный множитель земли и как его необходимо учитывать.
Рассмотрим как зависит интерференционный множитель земли от угла возвышения:
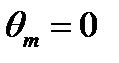 считаем, что ДН является симметричной:
считаем, что ДН является симметричной:
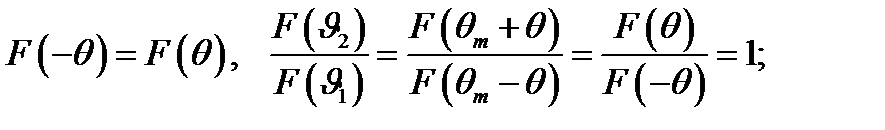

Следовательно ИМЗ(интерференционный множитель земли) приобретает вид:
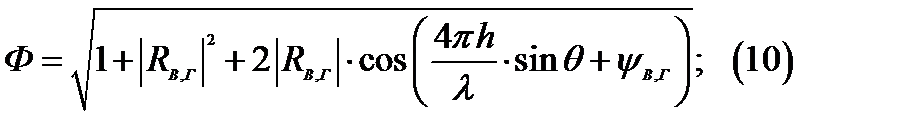
Пусть:
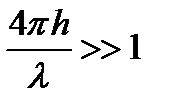 основное изменение будет определяться cos, т.к. cos при изменении угла
основное изменение будет определяться cos, т.к. cos при изменении угла 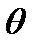 быстрее меняется, чем модуль коэффициента отражения, как при вертикально, так и при горизонтальной поляризации. Нас интересуют точки, где ИМЗ принимает максимальное и минимальное значение:
быстрее меняется, чем модуль коэффициента отражения, как при вертикально, так и при горизонтальной поляризации. Нас интересуют точки, где ИМЗ принимает максимальное и минимальное значение:
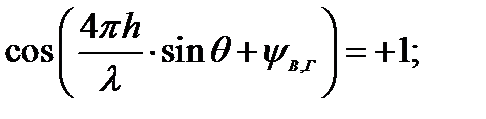 -макс.
-макс. 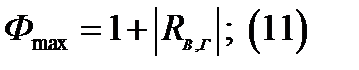
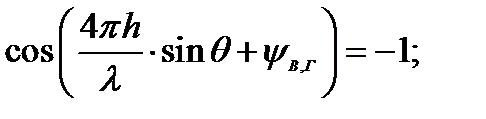 -мин;
-мин; 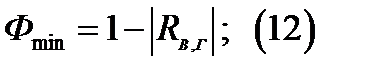
Далее нам необходимо учитывать поляризацию, т.к. из графиков приведенных выше на расчеты накладываются определенные условия, исходя из вида поляризации.
Горизонтальная поляризация. 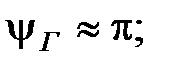
Углы в которых ИМЗ принимает максимальные и минимальные значения.
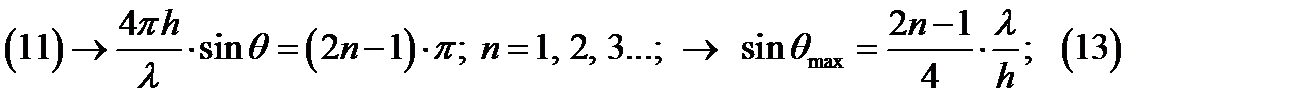
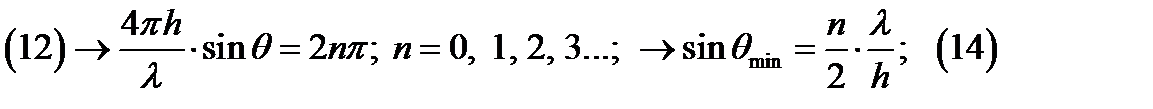
Анализируя (13) и (14) видно, что ИМЗ имеет лепестковый характер. Число лепестков можно определить по числу максимальных значений:
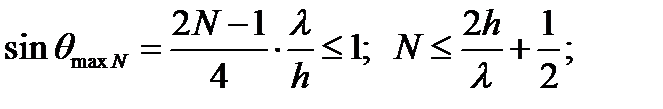
Число лепестков равно числу полуволн укладывающихся на высоте h.
Пример: 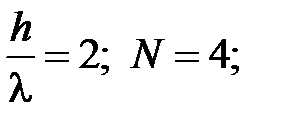
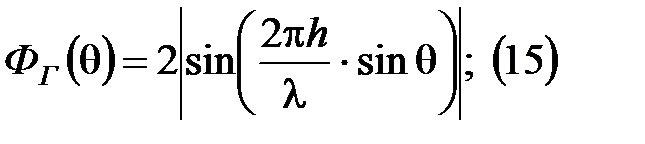

Анализ рис.7 показывает, чтобы увеличить дальность радиосвязи необходимо антенну поднимать.
Вертикальная поляризация:
При данной поляризации происходит скачек фазы, который необходимо учитывать.
ДН вертикального диполя:
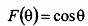
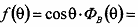
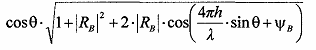
Проводник:
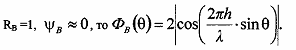
Отсюда рассматривая направления максимумов и минимумов и считая количество лепестков, получим, что количество лепестков определяется:
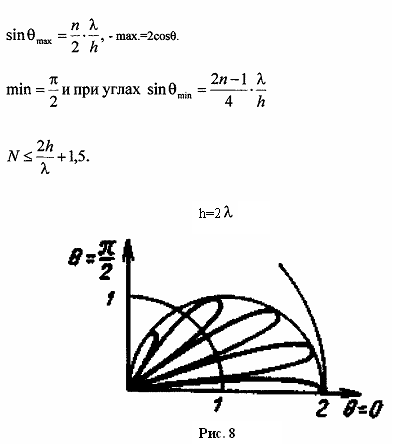
Из рис.8 видим, что нижний лепесток прижимается к земле, поэтому если нет возможности поднять антенну повыше, то лучше использовать вертикальную поляризацию(с точки зрения ИМЗ) но необходимо учитывать препятствия.
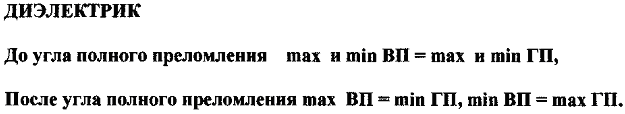
Для полупроводника также необходимо исходить из точных формул (11) и (12).
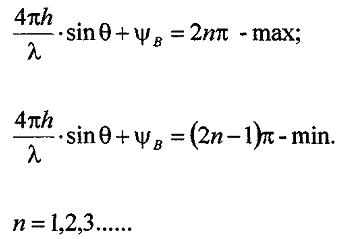
В данном случае модуль коэффициента отражения:
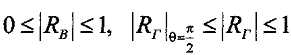
Вывод:
1)Поскольку ИМЗ при вертикальной и горизонтальной поляризациях описывается функция cos sin соответственно, то направление минимума ИМЗ при горизонтальной поляризации соответствуют направления максимумов при вертикальной поляризации и наоборот.
2) С увеличение высоты подъема антенны углы 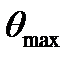 и
и 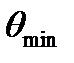 уменьшаются, т.е. лепестки ДН сильнее прижимаются к земле, и тем самым можно увеличить дальность радиосвязи.
уменьшаются, т.е. лепестки ДН сильнее прижимаются к земле, и тем самым можно увеличить дальность радиосвязи.
Общие сведения о физике ионосферы. Образование ионизированных слоев атмосферы. Простой ионосферный слой.
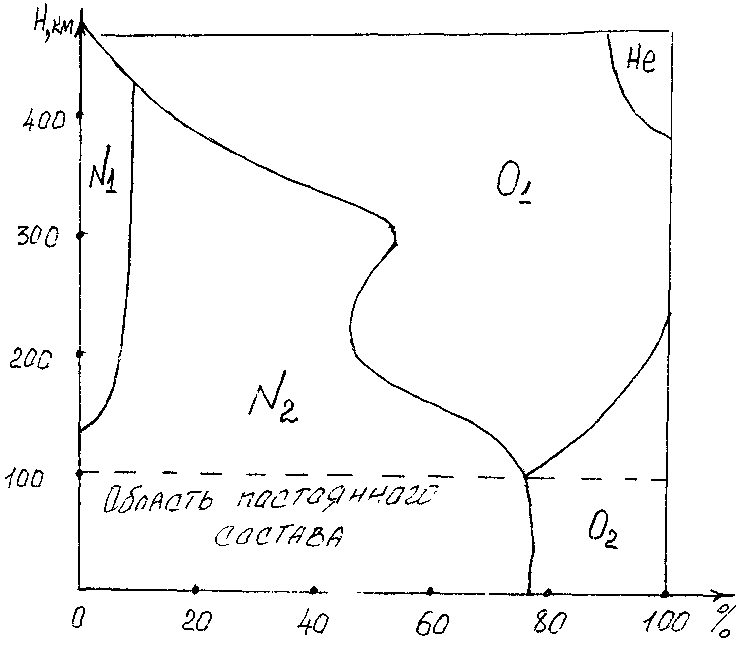 Ионосфера-ионизированный слой атмосферы, начинается с высоты 60 км, верхняя граница не имеет четкого выделения, примерно на 15 -20 тыс.км ионизированный слой плавно переходит в межпланетный газ. Ионосфера представляет собой диспергирующую, неоднородную, нестационарную, анизатропную среду.
Ионосфера-ионизированный слой атмосферы, начинается с высоты 60 км, верхняя граница не имеет четкого выделения, примерно на 15 -20 тыс.км ионизированный слой плавно переходит в межпланетный газ. Ионосфера представляет собой диспергирующую, неоднородную, нестационарную, анизатропную среду.
. В ионосфере:
Азот – 78%, кислород – 21%, аргон, гелий, криптон, ксенон – 0,9%, озон, радон, и др. - 0,1%.
В разряженной атмосфере под воздействием солнечной радиации происходит диссоциация кислорода и азота. Молекулы кислорода и азота расщепляются(кислород на кислород атомарный, а азот на азот атомарный) при поглощении кванта лучистой энергии расщепляются:
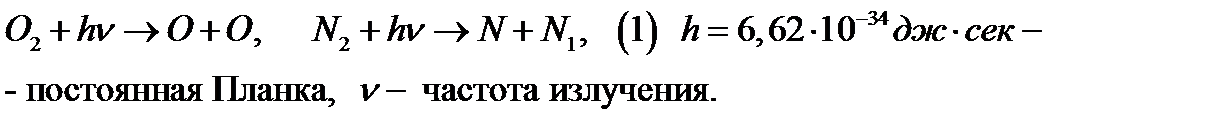
Энергия фотона, при которой происходит диссоциация кислорода, соответствует длине волны 0,24мкМ. Для азота 0,128мкМ. Спектр видимого света ограничен от 0,4 до 0,75мкМ, следовательно, диссоциация молекул кислорода и азота может происходить только под действие ультрафиолетового и рентгеновского излучения. Реакция диссоциации азота в 108 менее эффективна, чем диссоциация кислорода, поэтому наличие азота в верхних слоях атмосферы оно обусловлено другими более сложными фотохимическими реакциями. Диссоциация кислорода происходит с высот порядка 90км, а реакции, приводящие к образованию атомарного азота с высоты порядка 200км.
Ионизация, образование положительных и отрицательных ионов и свободных электронов из электрически нейтральных атомов и молекул. Механизм ионизации – заключается в отрывании электронов от наружной оболочки атомов, после чего он обретает заряд. Что бы совершить работу по ионизации, необходимо затратить энергию. В данном случае особый интерес представляют фото-ионизация и ударная ионизация. Если конкретный газ подвергается действию лучистой энергии с энергией фотонов 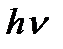 , работа по ионизации
, работа по ионизации 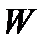 , то ионизация может произойти при соблюдении условия:
, то ионизация может произойти при соблюдении условия:
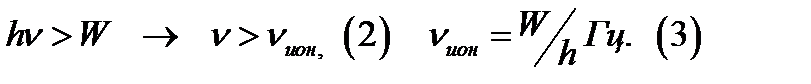
Неравенство (2) показывает, что ионизация рассматриваемого газа происходи, под воздействием излучения, частота которого превышает некоторое критическое значение, это кр. значение называют частотой ионизации. Ни какое увеличение интенсивности излучения( количества фотонов), частота которых не превышает частоту ионизации не может совершить работу по ионизации газа. При малых скоростях выбиваемых электронов, когда можно некоторыми поправками пренебречь, общий баланс энергии выражается равенством:
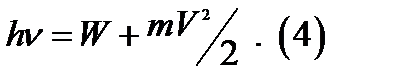 Увеличение частоты излучения при неизменно числе фотонов приводит к увеличению скорости выбиваемых электронов.- Фото-ионизация
Увеличение частоты излучения при неизменно числе фотонов приводит к увеличению скорости выбиваемых электронов.- Фото-ионизация
При ударной ионизации непосредственной причинно вырывания электрона является попадание в молекулу или атом частицы(корпускулы) обладающей достаточным запасом кинетической энергии. Условие ионизации запишется в виде:
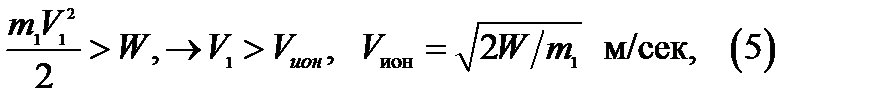
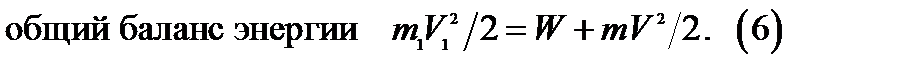
m1, V1 - масса и скорость ионизирующей частицы, m, V - масса и скорость выбитого электрона.
Связь между кинетической энергией и работой ионизации:
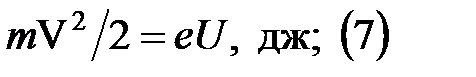 е – заряд электрона, U- разность потенциалов (В).
е – заряд электрона, U- разность потенциалов (В).
учитывая, что 1эв = 1,60207·10 –19 дж получим:
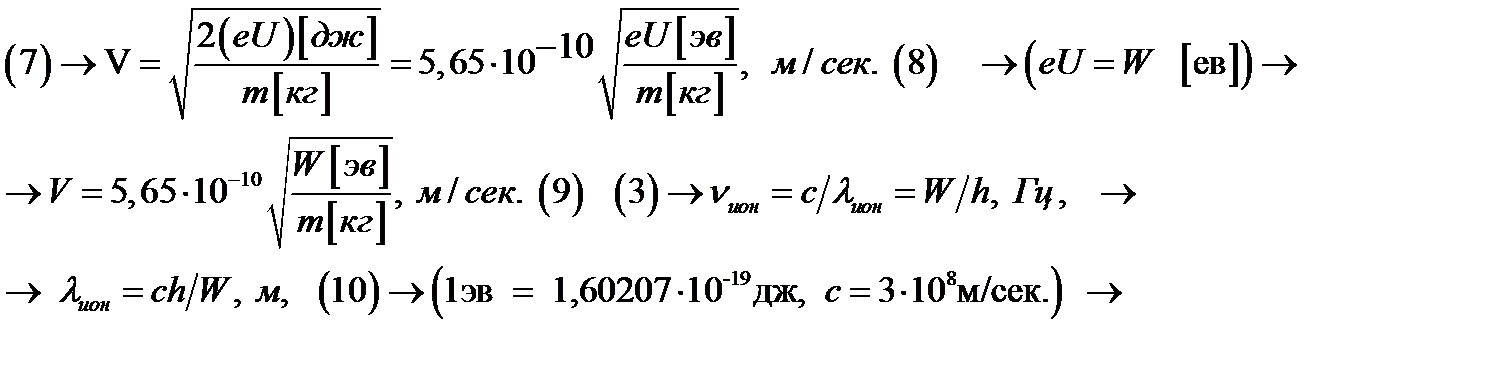
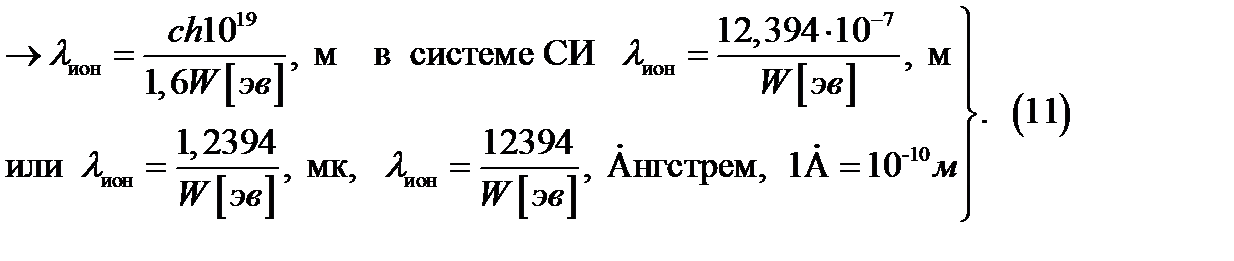

Таблица №1.
Зависимость концентрации электронов от высоты ионосферы. На больших высотах, плотность ионосферы мала, внизу плотность велика, но уже энергия солнца мала, потому что она растрачивается на ионизацию более верхних слоев.Таким образом наиболее ионизированным оказывается средний слой. Данное явление отображается на рисунке 2-простой ионосферный слой, где представлена зависимость концентрации ионов (N) от высоты. Т.о. максимум ионизации на высоте Zm-300-400км.

В реальной ионосфере различаются несколько слоев. D – возникает в дневное время суток. Периодически возникает спорадический слой Es. В ночное время D и F1 исчезают, остаются только Е и F2-электронная концентрация которых тоже меняется с наступлением темноты.

 Рис. 4. Предполагаемая зависимость кинетической температуры Атмосферы от высоты а). Ориентировочное распределение Электронной концентрации по высоте б).
Рис. 4. Предполагаемая зависимость кинетической температуры Атмосферы от высоты а). Ориентировочное распределение Электронной концентрации по высоте б).
В таблице нас интересует изменение электронной концентрации.
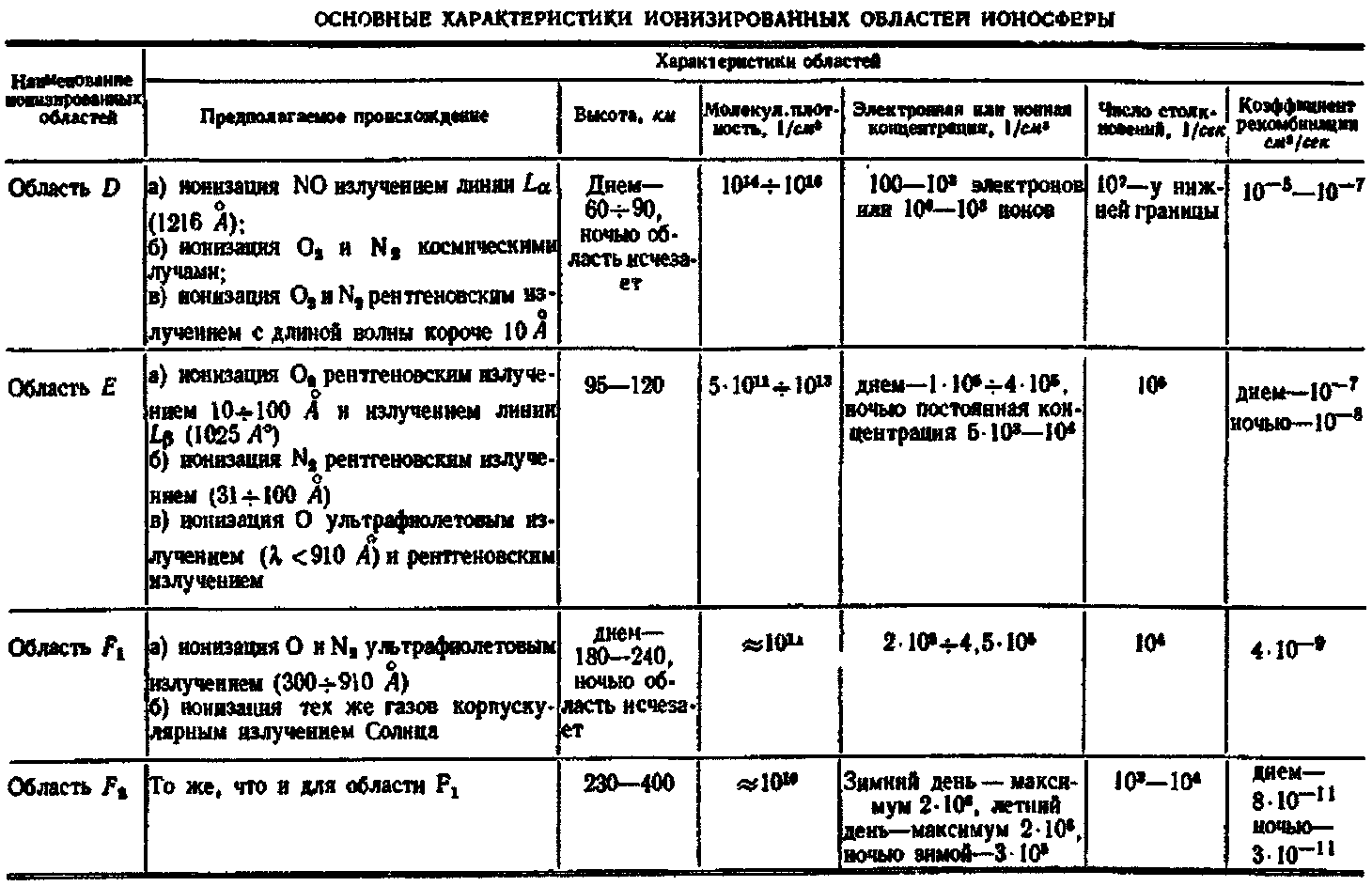
Основы теории цепей
Электрическая цепь. Элементы электрической цепи. Электрические схемы замещения физических устройств идеализированными элементами цепи. Схема электрической цепи (ветвь, узел, контур). Граф цепи.
Электрической цепью называется совокупность устройств, предназначенных для прохождения электрического тока и описываемых с помощью понятий напряжения и тока. Электрическая цепь состоит из источников (генераторов) и потребителей электромагнитной энергии – приемников или нагрузки.
Источником называют устройство, создающее (генерирующее) токи и напряжения. В качестве источников могут выступать устройства (аккумуляторы, гальванические элементы, термоэлементы, пьезодатчики, различные генераторы и т. д.), преобразующие различные виды энергии (химической, тепловой, механической, световой, молекулярно-кинетической и др.) в электрическую энергию. К источникам относятся и приемные антенны, в которых не происходит изменение вида энергии.
Приемником называют устройство, потребляющее (запасающее) или преобразующее электрическую энергию в другие виды энергии (тепловую, механическую, световую и т. д.). К приемникам относятся и передающие антенны, излучающие электромагнитную энергию в пространство. В теории цепей различают активные и пассивные элементы. Активными элементами считаются источники электрической энергии: источники напряжения и источники тока. К пассивным элементам относятся сопротивления, индуктивности и емкости. Цепи, содержащие активные элементы, называются активными, цепи, состоящие только из пассивных элементов – пассивными.
Пассивные элементы. Сопротивлением называется идеализированный элемент цепи, характеризующий преобразование электромагнитной энергии в любой другой вид энергии (тепловую – нагрев, механическую, излучение электромагнитной энергии и др.), т. е. обладающий только свойством необратимого рассеяния энергии. Реальный элемент, приближающийся по своим свойствам к сопротивлению, называется резистором.
Индуктивностью называется идеализированный элемент электрической цепи, характеризующий запасаемую в цепи энергию магнитного поля.
Емкостью называется идеализированный элемент электрической цепи, характеризующий запасаемую в цепи энергию электрического поля. Емкостью между электродами называется отношение потока вектора электрического смещения к разности потенциалов U на зажимах.
Схема электрической цепи
Схемой электрической цепи называется графически изображенная модель ее (рис. 2.1), составленная из идеализированных пассивных (R, L, C) и активных (e, i) элементов. Основными понятиями, характеризующими геометрическую конфигурацию цепи, являются ветвь, узел, контур.
Ветвь – участок цепи, образованный последовательно соединенными элементами. Последовательным соединением элементов цепи называется такое соединение, при котором через них проходит один и тот же ток.
Узел – точка соединения трех и более ветвей.
Контур – любой замкнутый путь, проходящий по нескольким ветвям. Параллельным соединением элементов называется такое соединение, при котором на них действует одно напряжение.

Ветви: ас – C1 R1 e1, аg – L1 R3 e2, ab – R2, bd – R4, dg – L3 и т. д.
Узлы: а, b, c, d, g.
Контуры: 1) a – b – c – a, 2) a – b – d – g – a, 3) b – d – g – c – b и т. д.
Граф цепи.
При исследовании процессов в сложных цепях существенное значение имеет геометрическая структура (топология), характеризуемая совокупностью узлов и ветвей, независимо от конкретных особенностей элементов.
В связи с этим наряду с понятием схемы цепи вводится понятие топологического графа или просто графа (как бы скелета схемы). Если на графе указывают направления токов, то граф называют направленным (рис. 2.2, б). Если граф не может быть изображен без пересечения ветвей, то он называется непланарным (рис. 2.2, в).
Очень важным понятием является так называемое дерево графа – любая система из минимального числа ветвей графа, соединяющая все узлы без образования контуров. Протекание тока по ветвям дерева исключается.
а) б) в)
Рис. 2.2
Таким образом, все ветви графа разбиваются на ветви дерева и не вошедшие в дерево – ветви связи (главные ветви или хорды).
Дата: 2019-07-23, просмотров: 900.