Основными законами электрических цепей, позволяющими описывать любые режимы их работы, являются закон Ома и законы Кирхгофа.

1. Закон Ома. Если сопротивление проводника R не зависит от величины и направления протекающего тока (сопротивление является линейным), то падение напряжения на нем пропорционально току i и сопротивлению R

U = R · i.

2. Закон Джоуля − Ленца. Если образующие цепь проводники неподвижны, а ток постоянен, то работа сторонних сил целиком расходуется на нагревание проводников

W _R = U · I · t,

соответствующее ей количество теплоты в калориях

W _R = 0,24·U · i · t.

3. Первый закон Кирхгофа. Алгебраическая сумма токов в ветвях, связанных общим узлом электрической цепи (рис. 2.4), равна нулю.

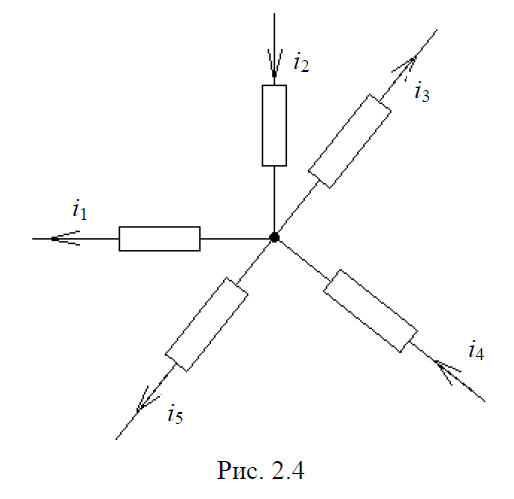
(Сумма токов, приходящих к узлу, равна сумме токов, уходящих от узла.)

Уходящие токи будем считать отрицательными, приходящие – положительными.

– i1 + i2 – i3 + i4 – i5 = 0 или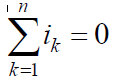

где k – номер ветви, связанной с данным узлом.

Первый закон Кирхгофа вытекает из того, что в узле не могут накапливаться и расходоваться заряды.

Первый закон Кирхгофа применим также к любому контуру или замкнутой поверхности, охватывающей часть электрической цепи, поскольку ни в каком элементе, ни в каком режиме заряды одного знака накапливаться не могут.

4. Второй закон Кирхгофа. В любом контуре электрической цепи алгебраическая сумма падений напряжения на элементах равна алгебраической сумме ЭДС, действующих в этом контуре:

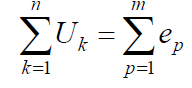
Второй закон Кирхгофа устанавливает баланс напряжений в контурах электрической цепи и вытекает из закона сохранения энергии. Действительно, если умножить обе части последнего уравнения на dq, то в левой части получим элементарную работу переноса заряда dq вдоль пассивных элементов цепи, а в правой – работу сил стороннего поля.

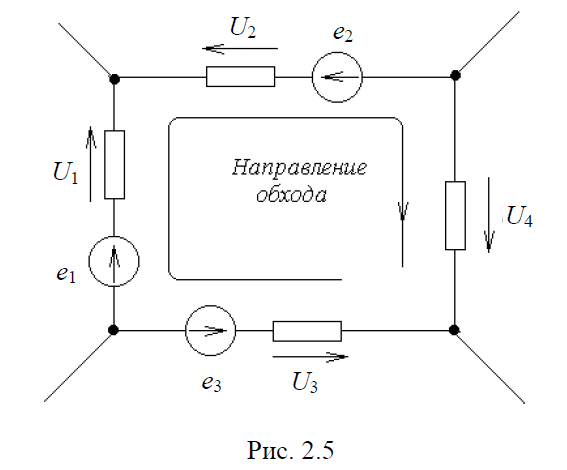
Напряжения и ЭДС в последнем уравнении берут со знаком (+), если их направление совпадает с направлением обхода контура (выбранным произвольно), и со знаком (–), если не совпадает. Например, для цепи (рис. 2.5)

U1 – U2 – U3 + U4 = e1 – e2 – e3.

Если предположить, что все пассивные элементы представляют собой сопротивления, то уравнение можно переписать, воспользовавшись законом Ома:

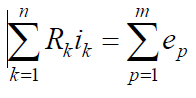
В общем случае, когда контур содержит сопротивления, индуктивности

и емкости и питание осуществляется источниками переменного напряжения,

уравнение второго закона Кирхгофа имеет вид

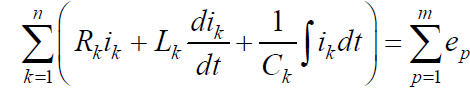
Расчёт сложных цепей. Применение законов Кирхгофа, метод контурных токов, метод наложения, метод узловых напряжений, метод эквивалентного генератора.