В некоторых случаях целесообразно использовать другие виды интерполяций. Например, если функция 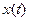 периодическая, то в качестве интерполирущего многочлена можно взять тригонометрический интерполяционный полином порядка
периодическая, то в качестве интерполирущего многочлена можно взять тригонометрический интерполяционный полином порядка 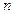 . Если в качестве системы линейно независимых функций
. Если в качестве системы линейно независимых функций 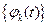 взять систему функций
взять систему функций
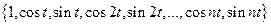 ,
,
то интерполяционный тригонометрический полином имеет вид
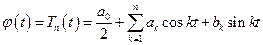 .
.
Для нахождения 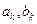 используют дискретное преобразование Фурье.
используют дискретное преобразование Фурье.
Дискретное преобразование Фурье – это одно из преобразований Фурье, широко применяемых в алгоритмах цифровой обработки сигналов (его гомоморфизмы применяются в сжатии звука в mp3, сжатие изображений в jpg и др.), а также в других областях, связанных с анализом частот в дискретном (к примеру, оцифрованном аналоговом) сигнале. Также дискретные преобразования Фурье помогают решать дифференциальные уравнения в частных производных и выполнять такие операции, как свёртки. Преобразования бывают одномерные, двумерные и даже трехмерные.
Последовательность 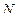 действительных чисел
действительных чисел 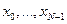 преобразовывается в последовательность из
преобразовывается в последовательность из 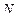 комплексных чисел
комплексных чисел 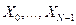 с помощью дискретного преобразования Фурье по формуле
с помощью дискретного преобразования Фурье по формуле
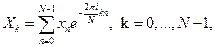
где 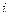 – это мнимая единица. Обратное дискретное преобразование Фурье задается формулой
– это мнимая единица. Обратное дискретное преобразование Фурье задается формулой
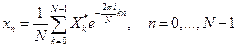 .
.
Поскольку напрямую вычисления дискретного преобразования требует 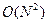 операций, то на практике используют более быстрый алгоритм быстрого преобразования Фурье, который требует
операций, то на практике используют более быстрый алгоритм быстрого преобразования Фурье, который требует 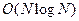 операций.
операций.
Дискретное преобразование Фурье является линейным преобразованием, которое переводит вектор временных отсчетов 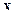 в вектор спектральных отсчетов той же длины. Таким образом, преобразование может быть реализовано как умножение квадратной матрицы на вектор:
в вектор спектральных отсчетов той же длины. Таким образом, преобразование может быть реализовано как умножение квадратной матрицы на вектор:
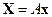 .
.
Матрица А имеет вид
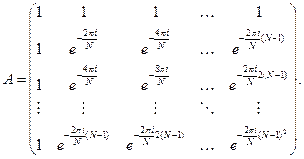
Свойства
1) линейность 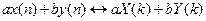 ;
;
2) сдвиг по времени 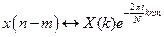 ;
;
3) периодичность 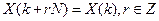 ;
;
4) выполняется теорема Парсеваля;
5) симметрия 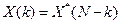 .
.
Таким образом, информацию несут первые 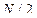 гармоник.
гармоник.
6) обладает спектральной плотностью 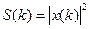 ;
;
7)  .
.
В случае четного числа  , из свойств 5,7 следует
, из свойств 5,7 следует
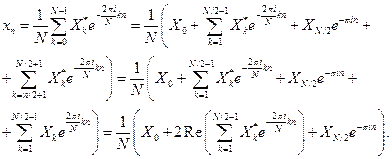
Переходим от дискретных значений 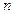 к непрерывному аргументу
к непрерывному аргументу 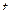 , таким образом, чтобы выполнялось равенство
, таким образом, чтобы выполнялось равенство 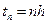 , при
, при 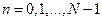 , где
, где 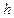 – шаг дискретизации. Формула в случае четного числа узлов для интерполяционного тригонометрического полинома запишется
– шаг дискретизации. Формула в случае четного числа узлов для интерполяционного тригонометрического полинома запишется
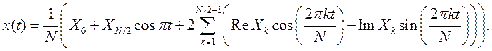
Аналогичным образом можно получить формулу для интерполяционного тригонометрического полинома в случае нечетного числа узлов, которая запишется следующим образом:
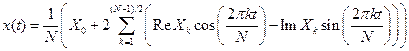 .
.
Пример выполнения практической работы №3
По заданной таблице 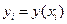 значений функции найти
значений функции найти 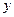 как функцию от
как функцию от 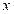 на основе:
на основе:
а) интерполяционного полинома Лагранжа и Ньютона;
б) интерполяционного кубического сплайна;
в) метода минимальных квадратов для линейной, квадратичной и кубической регрессии.
| X | 1 | 3 | 4 | 5 | 6 | 7 | 9 | 11 |
| Y | –1 | 2 | 3 | 9 | 4 | 7 | 2 | 7 |
г) интерполяционного тригонометрического полинома
| X | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| Y | 2 | –4 | 3 | 9 | –2 | 1 | 7 | 5 |
Дата: 2019-05-29, просмотров: 293.