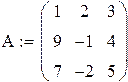
Задаем матрицу коэффициентов и столбец свободных членов
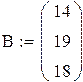
Проверяем невырожденность матрицы коэффициентов
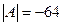 .
.
Определитель отличен от нуля, следовательно, матрица не вырождена.
Вводим функцию выбора главного элемента с последующим установлением его на главную диагональ
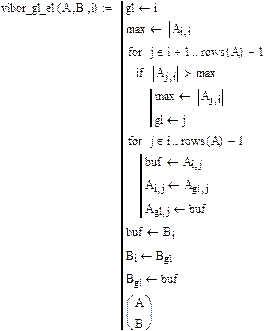
Вызываем функцию выбора главного элемента
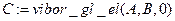 .
.
Выводим пример работы данной функции
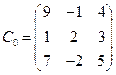
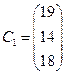
Вводим функцию, реализующую алгоритм прямого хода метода Гаусса с выбором главного элемента:
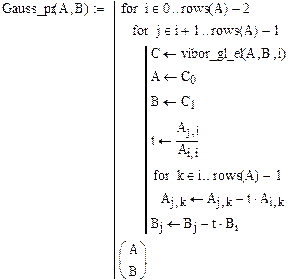
Вызываем данную функцию
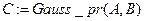 .
.
Выводим результат работы данной функции
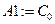
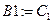
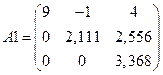 ,
, 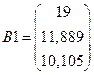 .
.
Вводим функцию, реализующую алгоритм обратного хода метода Гаусса:
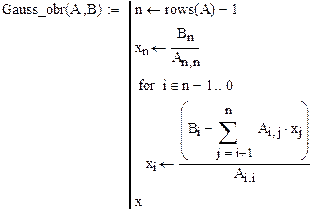
Вызываем данную функцию
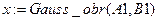 .
.
Выводим решение СЛАУ и делаем проверку
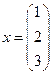 ,
, 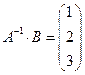 .
.
Метод LU -разложения для решения СЛАУ
Задаем матрицу коэффициентов и столбец свободных членов
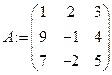 ,
, 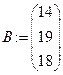 .
.
Вводим функцию, реализующую алгоритм LU-разложения:
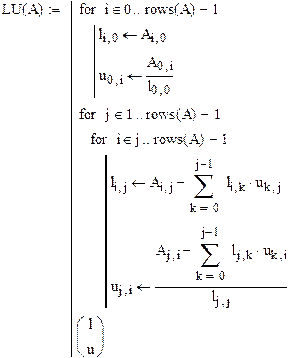
Вызываем данную функцию
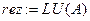 .
.
Выводим матрицы 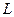 и
и 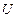 :
:
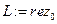 ,
, 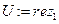 ,
,
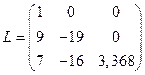 ,
, 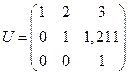 .
.
Делаем проверку
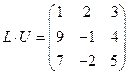 .
.
Вводим функцию, реализующую алгоритм обратного хода метода Гаусса с нижнетреугольной матрицей 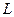 :
:
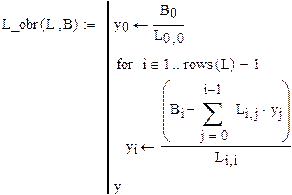
Вызываем данную функцию
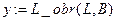 .
.
Выводим результат работы функции
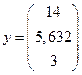 .
.
Вводим функцию, реализующую алгоритм обратного хода метода Гаусса с верхнетреугольной матрицей 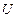 :
:
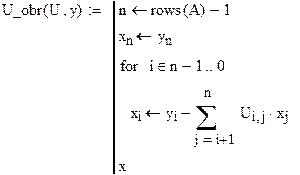
Вызываем данную функцию
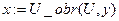 .
.
Выводим решение СЛАУ и делаем проверку
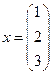 ,
, 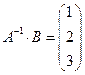 .
.
Метод прогонки для решения СЛАУ
Задаем диагонали матрицы коэффициентов и столбец свободных членов
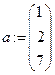 ,
, 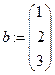 ,
,  ,
, 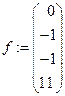 .
.
Вводим функцию, реализующую алгоритм прогонки:
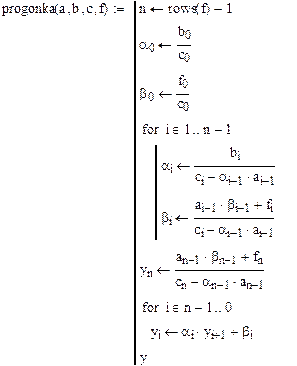
Выводим результат работы функции
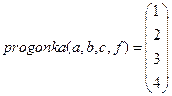 .
.
Варианты заданий к практической работе №1
Задание 1
Решите системы уравнений методом Гаусса и методом 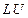 - разложения.
- разложения.
1) 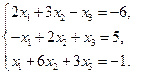 2)
2) 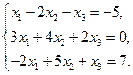
3) 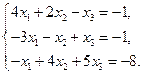 4)
4) 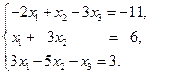
5) 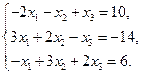 6)
6) 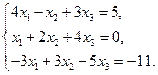
7) 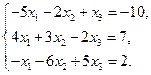 8)
8) 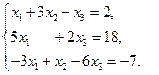
9) 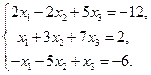 10)
10) 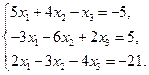
Задание 2
Решите системы уравнений методом прогонки.
1) 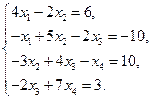 2)
2) 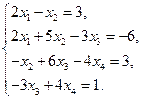
3) 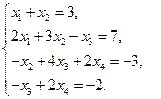 4)
4) 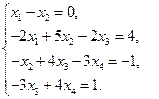
5) 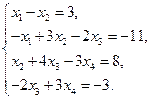 6)
6) 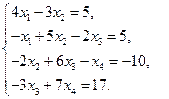
7) 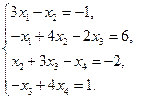 8)
8) 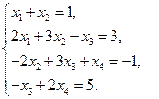
9) 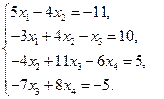 10)
10) 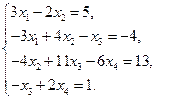
Содержание отчета
Отчет должен содержать:
1) титульный лист;
2) постановку задачи (согласно варианту);
3) краткое описание прямых методов расчета СЛАУ;
4) программную реализацию данных методов;
5) выводы о проделанной работе.
Контрольные вопросы и задания
1. Какие методы решения СЛАУ вы знаете?
2. Каково условие применимости метода Гаусса для решения СЛАУ?
3. Каково условие применимости метода LU-разложения?
4. Какой из алгоритмов: прямой или обратный ход метода Гаусса наиболее трудоемкий с точки зрения количества арифметических операций?
5. Получить оценки числа арифметических операций для решения СЛАУ методом Гаусса.
6. Получить оценки числа арифметических операций для решения СЛАУ методом LU-разложения.
7. Условие применимости метода прогонки.
8. Получить оценки числа арифметических операций для метода прогонки.
9*. В каком случае метод LU-разложения требует меньшего количества арифметических операций для решения СЛАУ, чем метод Гаусса?
10*. Как изменяется условие применимости метода Гаусса для решения СЛАУ, если не используется алгоритм выбора главного элемента?
Дата: 2019-05-29, просмотров: 313.