РОССИЙСКОЙ ФЕДЕРАЦИИ
Федеральное государственное автономное
образовательное учреждение высшего образования
«ЮЖНЫЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ»
 Кафедра интеллектуальных и
многопроцессорных систем Кафедра интеллектуальных и
многопроцессорных систем
| Т.В.Камышникова, А.В.Никитина, А.Е.Чистяков Непрерывные математические модели Учебно-методическое пособие для проведения практических работ |
 Таганрог
Таганрог
Издательство Южного федерального университета
2019
 |
УДК 517.949.8 (076.5)+
518.12 (076.5)
Никитина А.В., Кузнецова И.Ю.
Математические модели процессов и систем: учебно-методическое пособие. – Таганрог: Издательство ЮФУ, 2017. – 53 с.
Целью работы является обучение обучающихся работе с задачами, требующими большого объема вычислительной работы с использованием универсальных решающих программ типа MathCad.
Пособие предназначено для магистрантов всех специальностей, изучающих численные методы и современные проблемы прикладной математики и информатики.
Знаком * обозначены вопросы повышенной сложности.
Ил.: Библиогр.: назв.
Практическая работа №1. Прямые методы решения систем линейных алгебраических уравнений
Прямые методы теоретически позволяют за конечное число операций (действий) найти «точное» решение системы. Однако, в условиях вычислений на компьютерах, имеющих конечную разрядную сетку, прямые методы позволяют найти реально лишь приближенное решение системы, ввиду наличия погрешностей округления. Примерами прямых методов, рассматриваемых ниже, являются метод Гаусса и его модификации.
Алгоритм LU-разложения
Данный алгоритм можно рассматривать как конкретную форму метода Гаусса. Алгоритм LU-разложения используется не только для решения СЛАУ, но и также для обращения матрицы, т.е. вычисления матрицы, обратной данной.
Пусть 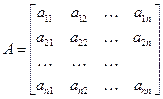 и будем искать представление
и будем искать представление  в виде
в виде
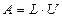 , ,
| (1.10) |
где 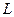 и
и 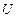 – соответственно нижняя и верхняя треугольные матрицы вида
– соответственно нижняя и верхняя треугольные матрицы вида
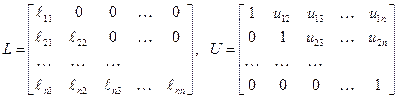 .
.
Известно, что если все угловые миноры матрицы 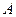 отличны от нуля, т.е.
отличны от нуля, т.е.
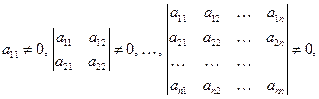
то разложение вида (1.10) существует и единственно. Для того чтобы получить расчётные формулы, поступим следующим образом. Обозначим 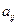 произведение
произведение 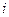 -ой строки матрицы
-ой строки матрицы 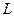 на
на 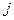 -й столбец матрицы
-й столбец матрицы 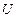 , причём будем считать вначале , что
, причём будем считать вначале , что 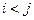 .
.
Тогда 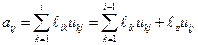 .
.
Выразим из последней формулы 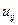 :
:
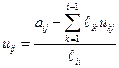 . .
| (1.11) |
Как это принято, будем считать в формуле (1.11) и далее, что сумма вида 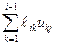 равна нулю, если значение верхней границы индекса суммирования меньше нижней границы.
равна нулю, если значение верхней границы индекса суммирования меньше нижней границы.
В случае 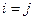 имеем
имеем
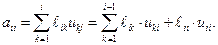
Учитывая, что 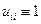 , и выражая из последнего соотношения
, и выражая из последнего соотношения 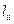 , получаем:
, получаем:
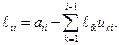 . .
| (1.12) |
Наконец, при 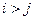 получаем
получаем
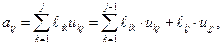
откуда, с учетом того, что 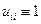 , приходим к формуле
, приходим к формуле
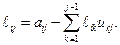 . .
| (1.13) |
Итак, расчетные формулы (1.11) – (1.13) получены. Для того чтобы при их применении не использовались неизвестные (не вычисленные) величины, необходимо выбрать соответствующий порядок вычисления элементов матриц 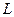 и
и 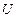 .
.
Например, можно рекомендовать порядок расчета элементов матриц 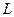 и
и 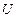 , схематически изображенный на рис. 1.1. На нем цифры слева для матрицы
, схематически изображенный на рис. 1.1. На нем цифры слева для матрицы 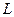 и сверху – для матрицы
и сверху – для матрицы 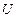 означают, что на первом шаге рассчитывается
означают, что на первом шаге рассчитывается 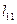 по формуле (1.12), затем вычисляется элемент
по формуле (1.12), затем вычисляется элемент 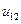 по формуле (1.11).
по формуле (1.11).
Далее (3 шаг) определяются элементы второй строки матрицы 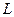 в порядке, указанном стрелкой:
в порядке, указанном стрелкой: 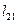 и
и 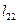 (по формулам (1.13) и (1.12) соответственно).
(по формулам (1.13) и (1.12) соответственно).
На 4 шаге выполняется расчет элементов 3 столбца матрицы 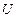 в порядке, обозначенном стрелкой:
в порядке, обозначенном стрелкой: 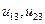 (формулы (1.11)) и т.д.
(формулы (1.11)) и т.д.
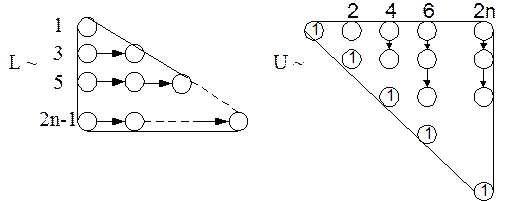
Рис. 1.1. Порядок расчета элементов матриц 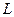 и
и 
Рассмотрим теперь применение LU-разложения для решения СЛАУ вида
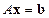 ,
,
где
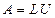 .
.
Введем вспомогательный вектор 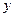 :
:
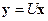 . .
| (1.14) |
Тогда исходную систему можно записать так
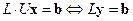 . .
| (1.15) |
В силу формул (1.14) и (1.15) решение исходной СЛАУ сводится к последовательному решению систем (1.15) и (1.14) соответственно с верхней и нижней треугольной матрицами.
Метод прогонки
Метод прогонки представляет собой вариант метода Гаусса, примененный к специальным системам линейных алгебраических уравнений и учитывающий ленточную структуру матрицы системы. Пусть имеем СЛАУ со специальной трехдиагональной формой матрицы:
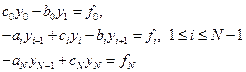
| (1.16) |
или в матричной форме: 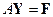 , где
, где 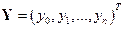 – вектор неизвестных;
– вектор неизвестных; 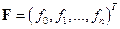 – вектор правых частей;
– вектор правых частей; 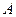 – квадратная
– квадратная 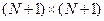 матрица:
матрица:
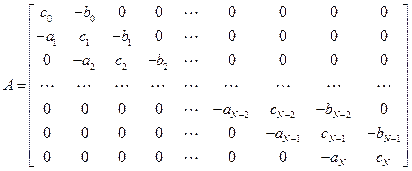
Системы вида (1.16) возникают при конечно-разностной аппроксимации краевых задач математической физики, описываемых обыкновенными дифференциальными уравнениями второго порядка с постоянными и переменными коэффициентами, а также уравнениями в частных производных. Ставится задача разработать экономичные методы решения задач вида (1.16), число арифметических операций для которых пропорционально числу неизвестных. Таким методом для системы (1.16) является метод прогонки. Специфика матрицы 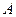 состоит в расположении ненулевых элементов, матрица
состоит в расположении ненулевых элементов, матрица 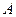 – разреженная матрица, из
– разреженная матрица, из 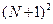 элементов которой ненулевыми являются не более
элементов которой ненулевыми являются не более 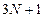 элементов. Это позволяет получить для решения СЛАУ простые расчетные формулы.
элементов. Это позволяет получить для решения СЛАУ простые расчетные формулы.
Будем искать решение (1.16) в виде
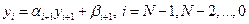
| (1.17) |
с неопределенными коэффициентами 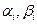 . Выражение
. Выражение 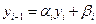 подставим в (1.16):
подставим в (1.16):
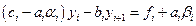 ,
,
c учетом (1.17) имеем
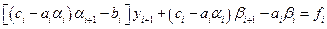 .
.
Это равенство имеет место для любых 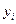 , если
, если
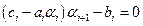 ,
, 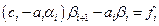 .
.
Отсюда получаем рекуррентные формулы для определения 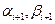 :
:
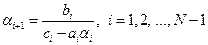 ; ;
| (1.18) |
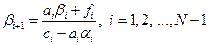 . .
| (1.19) |
Коэффициенты 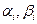 ,
, 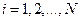 называются прогоночными.
называются прогоночными.
Если коэффициенты 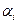 и
и 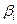 известны, а также известно
известны, а также известно 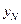 , то, двигаясь справа налево (от
, то, двигаясь справа налево (от 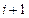 к
к 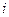 ) последовательно определяем все
) последовательно определяем все 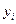 . Задача нахождения
. Задача нахождения 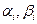 по формулам (1.18), (1.19) решается слева направо (от
по формулам (1.18), (1.19) решается слева направо (от 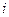 к
к 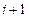 ). Начальные значения прогоночных коэффициентов
). Начальные значения прогоночных коэффициентов 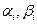 можно определить следующим образом. Полагаем в формуле (1.17)
можно определить следующим образом. Полагаем в формуле (1.17) 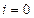 , имеем
, имеем 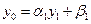 , а из первого уравнения (3.16)
, а из первого уравнения (3.16) 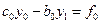 , откуда
, откуда
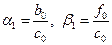 . .
| (1.20) |
Значение 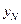 определяется следующим образом. Полагаем в формуле (1.17)
определяется следующим образом. Полагаем в формуле (1.17) 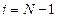 , имеем
, имеем 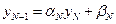 , а из последнего уравнения (3.18) –
, а из последнего уравнения (3.18) –
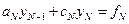 ,
,
откуда
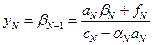 . .
| (1.21) |
Расчетные формулы (1.17) – (1.21) можно получить также из (1.16), если применить метод исключения Гаусса. Прямой ход метода заключается в том, что на первом шаге из всех уравнений системы (1.16) при помощи первого уравнения исключается 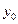 , затем из преобразованных уравнений для
, затем из преобразованных уравнений для 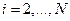 при помощи уравнения, соответствующего
при помощи уравнения, соответствующего 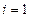 , исключается
, исключается 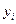 и т.д. В результате получим одно уравнение относительно
и т.д. В результате получим одно уравнение относительно 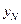 . На этом прямой ход метода прогонки заканчивается. На обратном ходе для
. На этом прямой ход метода прогонки заканчивается. На обратном ходе для 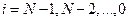 находятся
находятся 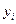 .
.
Порядок счета в методе прогонки следующий:
1) исходя из значений 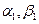 , вычисленных по формулам (1.20), все остальные коэффициенты
, вычисленных по формулам (1.20), все остальные коэффициенты 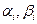 для
для 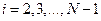 определяются последовательно по формулам (1.18) и (1.19);
определяются последовательно по формулам (1.18) и (1.19);
2) исходя из значения 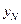 , рассчитанного по формуле (1.21), все остальные неизвестные
, рассчитанного по формуле (1.21), все остальные неизвестные 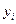 ,
, 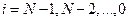 определяются последовательно по формуле (1.17).
определяются последовательно по формуле (1.17).
Изложенный метод поэтому называется правой прогонкой.
Аналогично выводятся формулы левой прогонки:
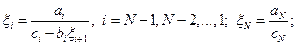
| (1.22) |
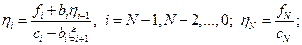
| (1.23) |
| yi+1 = xi+1yi + hi+1, i = N-1, N-2, …, 0; y0 = h0. | (1.24) |
Здесь 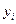 находятся последовательно для значений
находятся последовательно для значений 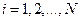 ; ход вычислений – слева направо.
; ход вычислений – слева направо.
В случае, если необходимо найти только одно неизвестное, например, 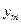
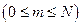 или группу идущих подряд неизвестных, целесообразно комбинировать правую и левую прогонки. При этом получается метод встречных прогонок.
или группу идущих подряд неизвестных, целесообразно комбинировать правую и левую прогонки. При этом получается метод встречных прогонок.
Произведем подсчет числа арифметических действий для метода правой прогонки. Анализ формул (1.17) – (1.21) показывает, что общее число арифметических операций есть 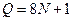 . Коэффициенты
. Коэффициенты 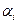 не зависят от правой части СЛАУ (1.16) и определяются только элементами
не зависят от правой части СЛАУ (1.16) и определяются только элементами 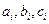 матрицы
матрицы 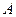 . Поэтому, если требуется решить серию задач (1.16) с различными правыми частями, то прогоночные коэффициенты
. Поэтому, если требуется решить серию задач (1.16) с различными правыми частями, то прогоночные коэффициенты 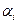 вычисляются только для первой серии. Для каждой последующей серии задач определяются только коэффициенты
вычисляются только для первой серии. Для каждой последующей серии задач определяются только коэффициенты 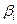 и решение
и решение 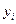 , причем используются ранее найденные
, причем используются ранее найденные 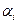 .
.
На решение первой из серии задач расходуется 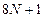 операций, а на решение каждой следующей задачи –
операций, а на решение каждой следующей задачи – 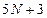 операций. Число арифметических операций, необходимое для решения СЛАУ (1.16) методом левой прогонки и методом встречных прогонок, такое же, т.е.
операций. Число арифметических операций, необходимое для решения СЛАУ (1.16) методом левой прогонки и методом встречных прогонок, такое же, т.е. 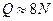 . Метод правой прогонки будем называть корректным, если
. Метод правой прогонки будем называть корректным, если 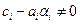 при
при 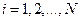 .
.
Решение 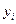 находится по рекуррентной формуле (1.17). Эта формула может порождать накопление ошибок округления результатов арифметических операций. Пусть прогоночные коэффициенты
находится по рекуррентной формуле (1.17). Эта формула может порождать накопление ошибок округления результатов арифметических операций. Пусть прогоночные коэффициенты 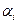 и
и 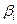 найдены точно, а при вычислении
найдены точно, а при вычислении 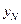 допущена ошибка
допущена ошибка 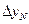 , т.е.
, т.е. 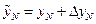 . При вычислениях с помощью формулы (1.17) мы получаем
. При вычислениях с помощью формулы (1.17) мы получаем
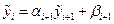 . .
| (1.25) |
Вычитая из (1.25) значение yi по формуле (1.17), имеем для погрешности 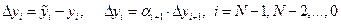 с заданным
с заданным 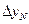 . Отсюда ясно, что если
. Отсюда ясно, что если 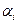 по модулю больше единицы и если
по модулю больше единицы и если 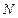 достаточно велико, то вычисленное значение
достаточно велико, то вычисленное значение 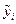 будет значительно отличаться от искомого решения
будет значительно отличаться от искомого решения 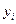 . В этом случае говорят, что алгоритм прогонки неустойчив.
. В этом случае говорят, что алгоритм прогонки неустойчив.
Определение. Алгоритм прогонки называется устойчивым, если 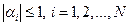 .
.
Условия корректности и устойчивости алгоритма правой прогонки определяются следующей теоремой.
Теорема. Пусть коэффициенты системы (1.16) действительны и удовлетворяют условиям:
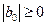 ,
, 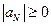 ,
, 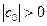 ,
, 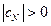 ,
, 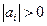 ,
, 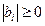 ,
, 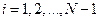 ;
;
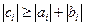 , , 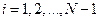 ; ;
| (1.26) |
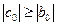 , , 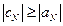 , ,
| (1.27) |
причем хотя бы в одном из неравенств (1.26) и (1.27) выполняется строгое неравенство, т.е. матрица А имеет диагональное преобладание. Тогда для алгоритма (1.17) – (1.21) имеют место неравенства: 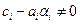 ,
, 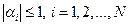 , т.е. алгоритм метода правой прогонки корректен и устойчив.
, т.е. алгоритм метода правой прогонки корректен и устойчив.
Условия (1.26) и (1.27) теоремы обеспечивают также корректность и устойчивость алгоритмов левой и встречных прогонок. Эти условия сохраняются и для случая системы (1.16) с комплексными коэффициентами 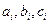 .
.
Легко показать, что при выполнении условий (1.26) – (1.27) теоремы система (1.16) имеет единственное решение при любой правой части.
Пример выполнения практической работы №1
Решите систему уравнений методом Гаусса и методом LU-разложения
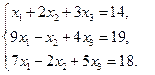
Решите систему уравнений методом прогонки
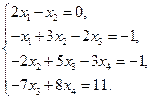
Варианты заданий к практической работе №1
Задание 1
Решите системы уравнений методом Гаусса и методом  - разложения.
- разложения.
1) 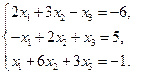 2)
2) 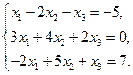
3) 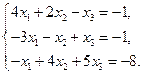 4)
4) 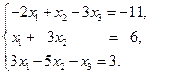
5) 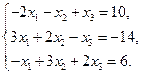 6)
6) 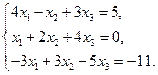
7) 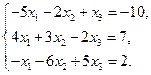 8)
8) 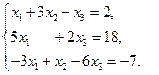
9) 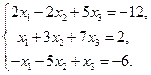 10)
10) 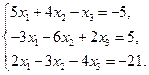
Задание 2
Решите системы уравнений методом прогонки.
1) 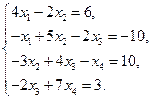 2)
2) 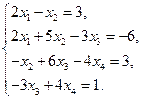
3) 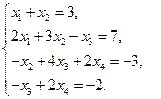 4)
4) 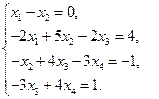
5) 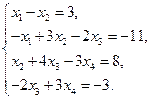 6)
6) 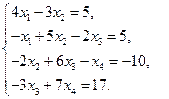
7) 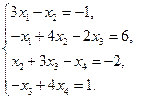 8)
8) 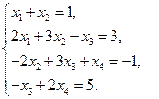
9) 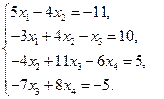 10)
10) 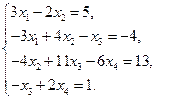
Содержание отчета
Отчет должен содержать:
1) титульный лист;
2) постановку задачи (согласно варианту);
3) краткое описание прямых методов расчета СЛАУ;
4) программную реализацию данных методов;
5) выводы о проделанной работе.
Контрольные вопросы и задания
1. Какие методы решения СЛАУ вы знаете?
2. Каково условие применимости метода Гаусса для решения СЛАУ?
3. Каково условие применимости метода LU-разложения?
4. Какой из алгоритмов: прямой или обратный ход метода Гаусса наиболее трудоемкий с точки зрения количества арифметических операций?
5. Получить оценки числа арифметических операций для решения СЛАУ методом Гаусса.
6. Получить оценки числа арифметических операций для решения СЛАУ методом LU-разложения.
7. Условие применимости метода прогонки.
8. Получить оценки числа арифметических операций для метода прогонки.
9*. В каком случае метод LU-разложения требует меньшего количества арифметических операций для решения СЛАУ, чем метод Гаусса?
10*. Как изменяется условие применимости метода Гаусса для решения СЛАУ, если не используется алгоритм выбора главного элемента?
Метод минимальных невязок
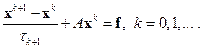
| (2.13) |
Для 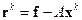 получим равенство, умножив обе части равенства (2.13) на матрицу
получим равенство, умножив обе части равенства (2.13) на матрицу 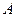 :
:
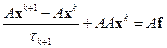 .
.
Меняя знаки и группируя слагаемые соответствующим образом, получаем:
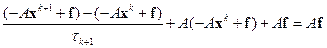 или
или
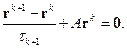
Параметр 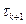 будем выбирать из условия минимума невязки
будем выбирать из условия минимума невязки 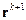 по норме
по норме
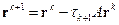 .
.
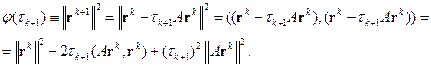
Продифференцируем 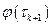 по
по 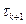 , получим
, получим
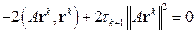 ,
,
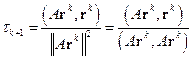 . .
| (2.14) |
Метод скорейшего спуска
Получается из условия минимума энергетической нормы погрешности 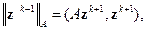 где
где 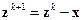 ,
, 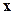 – точное решение исходной системы. Поскольку
– точное решение исходной системы. Поскольку 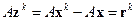 , и учитывая, что
, и учитывая, что
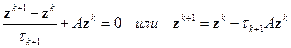 , получим
, получим
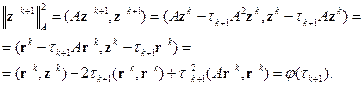
Дифференцируя 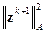 по
по 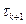 , получим
, получим
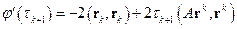 , откуда
, откуда
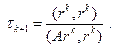
| (2.15) |
Пример выполнения практической работы №2
Решите систему уравнений методом Якоби, Зейделя, наименьших невязок и методом скорейшего спуска
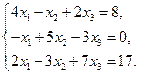
Варианты заданий к практической работе №2
Решите системы уравнений итерационными методами
1) 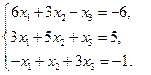 2)
2) 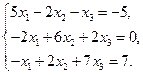
3) 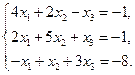 4)
4) 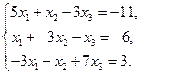
5) 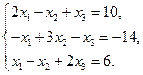 6)
6) 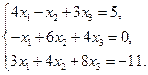
7) 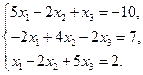 8)
8) 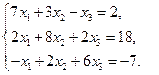
9) 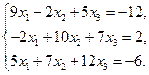 10)
10) 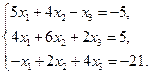
Содержание отчета
Отчет должен содержать:
1) титульный лист;
2) постановку задачи (согласно варианту);
3) краткое описание итерационных методов расчета СЛАУ;
4) программную реализацию данных методов;
5) выводы о проделанной работе.
Контрольные вопросы и задания
1. Какие методы решения СЛАУ вы знаете?
2. Запишите каноническую форму одношаговых (двухслойных) итерационных схем.
3. От чего зависит скорость сходимости итерационных методов?
4. Какие преимущества у вариационно-итерационных методов?
5. Каким образом определяется окончание итераций?
6. Запишите метод Якоби в векторной форме.
7. Запишите метод Зейделя в векторной форме.
8. Запишите формулу расчета итерационного параметра согласно методу скорейшего спуска.
9*. Условие применимости метода минимальных невязок.
10*. Условие применимости метода скорейшего спуска.
Свойства
1) линейность 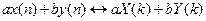 ;
;
2) сдвиг по времени 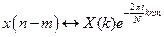 ;
;
3) периодичность 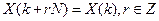 ;
;
4) выполняется теорема Парсеваля;
5) симметрия 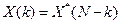 .
.
Таким образом, информацию несут первые 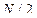 гармоник.
гармоник.
6) обладает спектральной плотностью 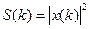 ;
;
7)  .
.
В случае четного числа 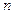 , из свойств 5,7 следует
, из свойств 5,7 следует
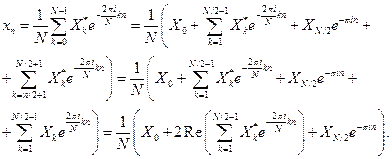
Переходим от дискретных значений 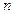 к непрерывному аргументу
к непрерывному аргументу 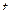 , таким образом, чтобы выполнялось равенство
, таким образом, чтобы выполнялось равенство 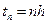 , при
, при 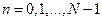 , где
, где 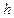 – шаг дискретизации. Формула в случае четного числа узлов для интерполяционного тригонометрического полинома запишется
– шаг дискретизации. Формула в случае четного числа узлов для интерполяционного тригонометрического полинома запишется
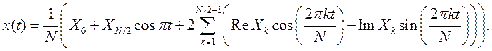
Аналогичным образом можно получить формулу для интерполяционного тригонометрического полинома в случае нечетного числа узлов, которая запишется следующим образом:
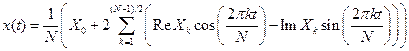 .
.
Пример выполнения практической работы №3
По заданной таблице 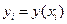 значений функции найти
значений функции найти 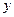 как функцию от
как функцию от 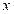 на основе:
на основе:
а) интерполяционного полинома Лагранжа и Ньютона;
б) интерполяционного кубического сплайна;
в) метода минимальных квадратов для линейной, квадратичной и кубической регрессии.
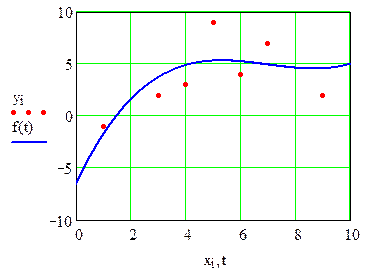
| X | 1 | 3 | 4 | 5 | 6 | 7 | 9 | 11 |
| Y | –1 | 2 | 3 | 9 | 4 | 7 | 2 | 7 |
г) интерполяционного тригонометрического полинома
| X | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| Y | 2 | –4 | 3 | 9 | –2 | 1 | 7 | 5 |
Метод наименьших квадратов
Задаем таблицу значений функции
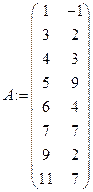
Устанавливаем счетчики
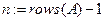 .
.
Считаем значения 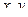
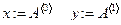 .
.
Задаем СЛАУ согласно методу минимальных квадратов в случае линейной регрессии
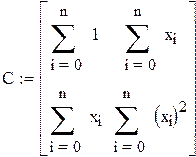
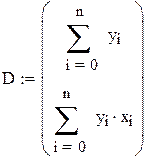
Решаем СЛАУ
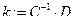 .
.
Строим линейную регрессионную функцию
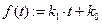 .
.
Устанавливаем счетчики
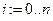 .
.
Строим график линейной регрессионной функции
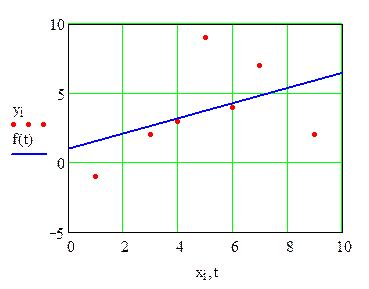
Считаем квадрат невязки
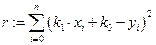 .
.
Считаем квадрат невязки
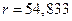 .
.
Задаем СЛАУ согласно методу минимальных квадратов в случае квадратичной регрессии
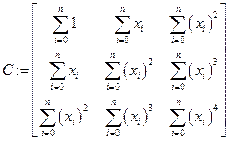 ;
; 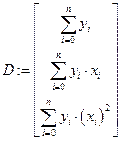 .
.
Решаем СЛАУ
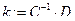 .
.
Строим квадратичную регрессионную функцию
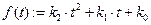 .
.
Строим график квадратичной регрессионной функции
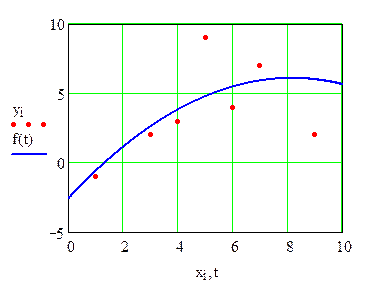
Считаем квадрат невязки
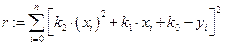 .
.
Считаем квадрат невязки
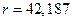 .
.
Задаем СЛАУ согласно методу минимальных квадратов в случае кубической регрессии
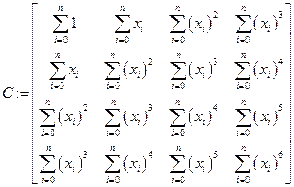 ;
; 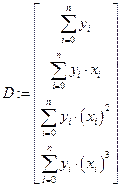 .
.
Решаем СЛАУ
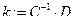 .
.
Строим кубическую регрессионную функцию
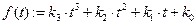 .
.
Строим график кубической регрессионной функции
Считаем квадрат невязки
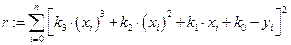 .
.
Считаем квадрат невязки
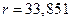 .
.
Варианты заданий к практической работе №3
По заданной таблице  значений функции найти
значений функции найти 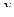 как функцию от
как функцию от 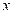 на основе:
на основе:
а) интерполяционного полинома Лагранжа и Ньютона;
б) интерполяционного кубического сплайна;
в) метода минимальных квадратов для линейной, квадратичной и кубической регрессии.
| Вариант | Значения функции | |||||||||
| 1 | x | 1 | 3 | 4 | 6 | 7 | 8 | 10 | 12 | 15 |
| y | 3 | 4 | 6 | 2 | 8 | 4 | 5 | 8 | 0 | |
| 2 | x | 1 | 2 | 5 | 6 | 7 | 9 | 11 | 12 | 16 |
| y | 2 | 6 | 3 | 2 | 4 | 5 | 5 | 9 | 3 | |
| 3 | x | 1 | 2 | 3 | 5 | 7 | 8 | 11 | 14 | 15 |
| y | –3 | 3 | 5 | 4 | 1 | –5 | 6 | 3 | 2 | |
| Вариант | Значения функции | |||||||||
| 4 | x | 1 | 2 | 4 | 6 | 7 | 10 | 12 | 14 | 17 |
| y | 3 | 4 | 6 | 3 | 8 | 1 | 2 | 3 | 7 | |
| 5 | x | 1 | 3 | 5 | 6 | 7 | 9 | 10 | 12 | 13 |
| y | 3 | 7 | 1 | 3 | –2 | 5 | –6 | 4 | 3 | |
| 6 | x | 1 | 3 | 5 | 6 | 7 | 9 | 11 | 13 | 18 |
| y | 3 | 5 | 9 | 2 | –1 | –4 | 3 | 4 | 8 | |
| 7 | x | 1 | 3 | 5 | 6 | 7 | 9 | 12 | 14 | 17 |
| y | 4 | 8 | 2 | 0 | 7 | 8 | –1 | 2 | 3 | |
| 8 | x | 1 | 3 | 4 | 6 | 7 | 8 | 11 | 15 | 18 |
| y | 3 | 5 | 8 | 3 | 7 | 1 | 9 | 3 | 2 | |
| 9 | x | 1 | 2 | 3 | 6 | 7 | 9 | 10 | 13 | 15 |
| y | 4 | 8 | 2 | 7 | –1 | 2 | 4 | 8 | 3 | |
| 10 | x | 1 | 3 | 5 | 6 | 7 | 8 | 10 | 12 | 17 |
| y | 3 | 5 | –1 | 7 | 3 | 6 | 9 | 0 | 4 | |
г) интерполяционного тригонометрического полинома
| Вариант | y(0) | y(1) | y(2) | y(3) | y(4) | y(5) | y(6) | y(7) |
| 1 | 4 | 6 | 8 | 3 | –4 | 3 | 2 | – |
| 2 | 3 | 4 | 4 | 7 | –4 | 3 | –3 | 3 |
| 3 | 4 | 3 | 9 | 4 | 1 | 3 | 6 | – |
| 4 | 6 | 1 | 5 | 8 | 7 | 2 | 3 | 4 |
| 5 | 7 | 9 | 7 | 6 | 3 | –4 | –5 | – |
| 6 | 3 | –4 | 2 | 3 | 5 | –4 | 2 | 3 |
| 7 | 2 | 4 | –5 | –2 | 4 | 3 | 6 | – |
| 8 | 9 | 5 | 0 | 9 | 3 | 6 | 5 | –5 |
| 9 | 6 | 8 | 0 | 5 | 3 | 5 | 7 | – |
| 10 | 4 | 5 | 6 | 3 | 6 | 8 | 7 | 4 |
Содержание отчета
Отчет должен содержать:
1) титульный лист;
2) постановку задачи (согласно варианту);
3) краткое описание методов решения задачи Коши;
4) программную реализацию данных методов;
5) выводы о проделанной работе.
Контрольные вопросы и задания
1. Какие виды приближения функции вы знаете?
2. Какие виды интерполяции функции вы знаете?
3. Приведите пример построения интерполяционного полинома при помощи метода Лагранжа.
4. Приведите пример построения интерполяционного полинома при помощи метода Ньютона.
5. Какой метод построения интерполяционного полинома является менее трудоемким: метод Лагранжа или метод Ньютона?
6. По заданной выборке найти оптимальную прямую методом наименьших квадратов.
7. По заданной выборке найти оптимальную параболу методом наименьших квадратов.
8. Приведите пример построения интерполяционного кубического сплайна.
9. Приведите пример построения интерполяционного тригонометрического полинома.
10. Как изменится трудоемкость дискретного преобразования Фурье в случае использования алгоритма быстрого преобразования Фурье?
Практическое задание №4. Компьютерное моделирование в экологии
Рассматриваются модели классической экологии (взаимодействие популяций). Популяция – совокупность особей одного вида, существующих в одно и то же время и занимающих определенную территорию.
Взаимодействие особей внутри популяции определяется внутривидовой конкуренцией, взаимодействие между популяциями – межвидовой конкуренцией.
4.1. Внутривидовая конкуренция в популяции с дискретным размножением. Для популяций с дискретным размножением (некоторые виды растений, насекомых и т.д.) поколения четко разнесены во времени и особи разных поколений не сосуществуют. Численность такой популяции можно характеризовать числом 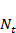 и считать
и считать  величиной дискретной – номером популяции.
величиной дискретной – номером популяции.
Одна из моделей межвидовой конкуренции в этом случае выражается уравнением
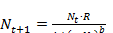 (4.1)
(4.1)
Здесь 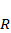 – скорость воспроизводства популяции в отсутствии внутривидовой конкуренции (математически это соответствует случаю
– скорость воспроизводства популяции в отсутствии внутривидовой конкуренции (математически это соответствует случаю 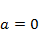 ). Тогда уравнение определяет просто изменение численности популяции по закону геометрической прогрессии:
). Тогда уравнение определяет просто изменение численности популяции по закону геометрической прогрессии: 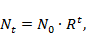 где
где 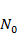 – начальная численность популяции.
– начальная численность популяции.
Знаменатель в уравнении отражает наличие конкуренции, делающей скорость роста тем меньше, чем больше численность популяции 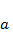 и
и 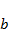 – параметры модели.
– параметры модели.
Исходные параметры модели:
• 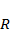 – скорость воспроизводства;
– скорость воспроизводства;
• 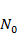 – начальная численность популяции;
– начальная численность популяции;
•  – параметр, характеризующий интенсивность внутривидовой конкуренции.
– параметр, характеризующий интенсивность внутривидовой конкуренции.
Характерная черта эволюции при 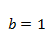 – выход численности популяции на стационарное значение при любых значениях других параметров. Однако, в природе так бывает не всегда и более общая модель при
– выход численности популяции на стационарное значение при любых значениях других параметров. Однако, в природе так бывает не всегда и более общая модель при 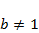 отражает другие, более сложные, но реально существующие, виды эволюции. Этих видов модель описывает четыре:
отражает другие, более сложные, но реально существующие, виды эволюции. Этих видов модель описывает четыре:
1) монотонное установление стационарной численности популяции;
2) колебательное установление стационарной численности популяции;
3) устойчивые предельные циклы изменения численности популяции;
4) случайные изменения численности популяции без наличия явных закономерностей (динамический хаос).
4.2. Внутривидовая конкуренция в популяции с непрерывным размножением. Математическая модель в данном случае строится на основе дифференциальных уравнений. Наиболее известна так называемая логистическая модель:
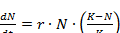 . (4.2)
. (4.2)
Исходные параметры модели:
•  – скорость роста численности популяции при отсутствии конкуренции;
– скорость роста численности популяции при отсутствии конкуренции;
• 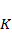 – предельное значение численности популяции, при котором скорость роста становится равной нулю;
– предельное значение численности популяции, при котором скорость роста становится равной нулю;
• 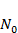 – начальная численность популяции.
– начальная численность популяции.
4.2.1 Межвидовая конкуренция. В этом случае исследуется конкуренция популяций, потребляющих общий ресурс. Пусть 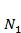 и
и 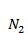 – численности конкурирующих популяций. Модель (называемая также моделью Лотки – Вольтерра) выражается уравнениями:
– численности конкурирующих популяций. Модель (называемая также моделью Лотки – Вольтерра) выражается уравнениями:
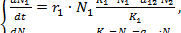 (4.3)
(4.3)
Содержательный смысл параметров можно понять из сравнения с предыдущей моделью. Дополнительные параметры 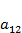 и
и 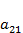 отражают интенсивность межвидовой конкуренции.
отражают интенсивность межвидовой конкуренции.
Главный вопрос, который интересует исследователя межвидовой конкуренции – при каких условиях увеличивается или уменьшается численность каждого вида? Данная модель предсказывает следующие режимы эволюции взаимодействующих популяций: устойчивое сосуществование или полное вытеснение одной из них.
4.2.2 Система «хищник – жертва». В этой системе ситуация значительно отличается от предыдущей. В частности, если в случае конкурирующих популяций исчезновение одной означает выигрыш для другой (дополнительные ресурсы), то исчезновение «жертвы» влечет за собой и исчезновение «хищника», для которого в простейшей модели «жертва» является единственным кормом.
Обозначим через 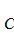 численность популяции хищника и через
численность популяции хищника и через 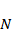 – популяции жертвы. Одна из известных моделей выражается следующими уравнениями:
– популяции жертвы. Одна из известных моделей выражается следующими уравнениями:
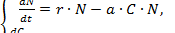 (4.4)
(4.4)
В первое уравнение заложен следующий смысл. При отсутствии хищников (т.е. при 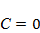 ) численность жертв растет экспоненциально со скоростью r, поскольку модель не учитывает внутривидовой конкуренции. Скорость роста числа жертв (т.е.
) численность жертв растет экспоненциально со скоростью r, поскольку модель не учитывает внутривидовой конкуренции. Скорость роста числа жертв (т.е. 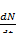 )
)
уменьшается тем больше, чем чаще происходят встречи представителей видов;  – коэффициент эффективности поиска.
– коэффициент эффективности поиска.
Второе уравнение говорит о следующем. При отсутствии жертв численность хищников экспоненциально убывает со скоростью  ;положительное слагаемое в правой части уравнения компенсирует эту убыль;
;положительное слагаемое в правой части уравнения компенсирует эту убыль; 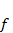 – коэффициент эффективности перехода пищи в потомство хищников.
– коэффициент эффективности перехода пищи в потомство хищников.
Задание 4.1
Вариант 1.
Изучить характер эволюции популяции, описываемый моделью (4.1), при значениях параметров 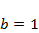 ,
, 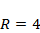 ,
, 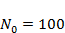 в зависимости от значения параметра а в диапазоне
в зависимости от значения параметра а в диапазоне 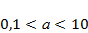 . Есть ли качественные различия в характере эволюции в зависимости от значения
. Есть ли качественные различия в характере эволюции в зависимости от значения  ?
?
Вариант 2.
Изучить характер эволюции популяции, описываемый моделью (4.1), при значениях параметров 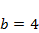 ,
, 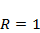 ,
, 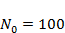 в зависимости от значения параметра а в диапазоне
в зависимости от значения параметра а в диапазоне 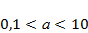 . Есть ли качественные различия в характере эволюции в зависимости от значения
. Есть ли качественные различия в характере эволюции в зависимости от значения  ?
?
Вариант 3.
Изучить характер эволюции популяции, описываемый моделью (4.1), при значениях параметров 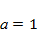 ,
, 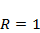 ,
, 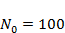 в зависимости от значения параметра
в зависимости от значения параметра 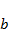 в диапазоне
в диапазоне 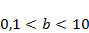 . Есть ли качественные различия в характере эволюции в зависимости от значения
. Есть ли качественные различия в характере эволюции в зависимости от значения 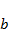 ?
?
Вариант 4.
Изучить характер эволюции популяции, описываемый моделью (4.1), при значениях параметров 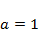 ,
, 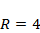 ,
, 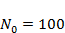 в зависимости от значения параметра
в зависимости от значения параметра 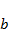 в диапазоне
в диапазоне 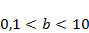 . Есть ли качественные различия в характере эволюции в зависимости от значения
. Есть ли качественные различия в характере эволюции в зависимости от значения 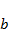 ?
?
Вариант 5.
Изучить характер эволюции популяции, описываемый моделью (4.1), при значениях параметров 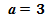 ,
, 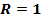 ,
, 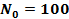 в зависимости от значения параметра
в зависимости от значения параметра 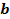 в диапазоне
в диапазоне 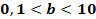 . Есть ли качественные различия в характере эволюции в зависимости от значения
. Есть ли качественные различия в характере эволюции в зависимости от значения 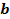 ?
?
Вариант 6.
Изучить характер эволюции популяции, описываемый моделью (4.1), при значениях параметров 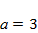 ,
, 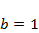 ,
, 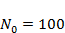 в зависимости от значения параметра
в зависимости от значения параметра 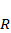 в диапазоне
в диапазоне 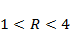 . Есть ли качественные различия в характере эволюции в зависимости от значения
. Есть ли качественные различия в характере эволюции в зависимости от значения 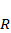 ?
?
Вариант 7.
Изучить характер эволюции популяции, описываемый моделью (4.1), при значениях параметров 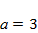 ,
, 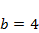 ,
, 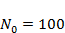 в зависимости от значения параметра
в зависимости от значения параметра 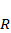 в диапазоне
в диапазоне 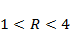 . Есть ли качественные различия в характере эволюции в зависимости от значения
. Есть ли качественные различия в характере эволюции в зависимости от значения 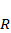 ?
?
Вариант 8.
Реализовать модель (4.1) при следующих наборах значений параметров:
1) 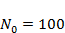 ,
, 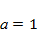 ,
, 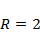 ,
, 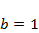 ;
;
2) 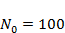 ,
, 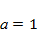 ,
, 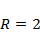 ,
,  ;
;
3) 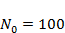 ,
, 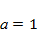 ,
, 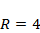 ,
, 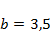 ;
;
4) 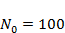 ,
, 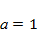 ,
, 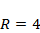 ,
, 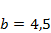
и изучить вид соответствующих режимов эволюции.
Вариант 9.
Для модели (4.1) в фазовой плоскости 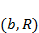 найти границы зон, разделяющих режим колебательного установления стационарной численности популяции изучаемой системы и режим устойчивых предельных циклов.
найти границы зон, разделяющих режим колебательного установления стационарной численности популяции изучаемой системы и режим устойчивых предельных циклов.
Вариант 10.
Изучить характер эволюции популяции, описываемый моделью (4.1), при значениях параметров 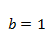 ,
, 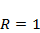 ,
, 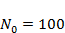 в зависимости от значения параметра а в диапазоне
в зависимости от значения параметра а в диапазоне 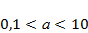 . Есть ли качественные различия в характере эволюции в зависимости от значения
. Есть ли качественные различия в характере эволюции в зависимости от значения 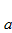 ?
?
Задание 4.2
Вариант 1.
Реализовать моделирование межвидовой конкуренции по формулам (4.3) при значениях параметров 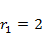 ,
, 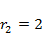 ,
, 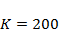 ,
, 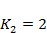 ,
, 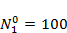 ,
, 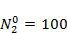 . Проанализировать зависимость судьбы популяций от соотношения значений коэффициентов конкуренции
. Проанализировать зависимость судьбы популяций от соотношения значений коэффициентов конкуренции 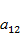 и
и 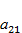 .
.
Вариант 2.
Построить в фазовой плоскости границы зон, разделяющих какие-либо два режима эволюции конкурирующих популяций (в соответствии с моделью (4.3)). Остальные параметры модели выбрать произвольно. Учесть при этом, что режим устойчивого сосуществования популяций может в принципе реализоваться только при 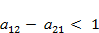 .
.
Вариант 3.
Провести моделирование динамики численности популяций в системе «хищник – жертва» (модель (4.4)) при значениях параметров 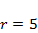 ,
, 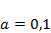 ,
, 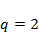 ,
, 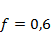 . Проанализировать зависимость исхода эволюции от соотношения значений параметров
. Проанализировать зависимость исхода эволюции от соотношения значений параметров 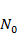 и
и 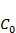 .
.
Вариант 4.
Провести моделирование динамики численности популяций в системе «хищник – жертва» (модель (4.4)) при значениях параметров 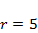 ,
, 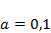 ,
, 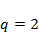 ,
, 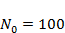 ,
, 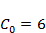 . Проанализировать зависимость результатов моделирования от значения параметра
. Проанализировать зависимость результатов моделирования от значения параметра 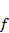 в диапазоне
в диапазоне 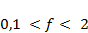 .
.
Вариант 5.
Провести моделирование динамики численности популяций в системе «хищник—жертва» (модель (4.4)) при значениях параметров 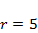 ,
, 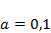 ,
, 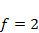 ,
, 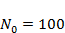 ,
, 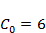 . Проанализировать зависимость результатов моделирования от значения параметра
. Проанализировать зависимость результатов моделирования от значения параметра  в диапазоне
в диапазоне 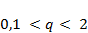 .
.
Вариант 6.
Провести моделирование динамики численности популяций в системе «хищник – жертва» (модель (4.4)) при значениях параметров 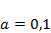 ,
, 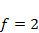 ,
, 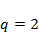 ,
, 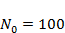 ,
, 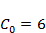 . Проанализировать зависимость результатов моделирования от значения параметра qв диапазоне
. Проанализировать зависимость результатов моделирования от значения параметра qв диапазоне 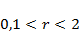 .
.
Вариант 7.
Модель (4.4) предсказывает сопряженные колебания численности жертв и хищников. Исследовать зависимость запаздывания амплитуд колебаний численности хищников от амплитуд колебаний численности жертв в зависимости от значений параметра  . Значения остальных параметров фиксировать по усмотрению.
. Значения остальных параметров фиксировать по усмотрению.
Вариант 8.
Модель (4.4) предсказывает сопряженные колебания численности жертв и хищников. Исследовать зависимость запаздывания амплитуд колебаний численности хищников от амплитуд колебаний численности жертв в зависимости от значений параметра  .Значения остальных параметров фиксировать по усмотрению.
.Значения остальных параметров фиксировать по усмотрению.
Вариант 9.
Модель (4.4) предсказывает сопряженные колебания численности жертв и хищников. Исследовать зависимость запаздывания амплитуд колебаний численности хищников от амплитуд колебаний численности жертв в зависимости от значений параметра 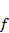 .Значения остальных параметров фиксировать по усмотрению.
.Значения остальных параметров фиксировать по усмотрению.
Вариант 10.
Реализовать моделирование межвидовой конкуренции по формулам (4.3) при значениях параметров 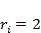 ,
, 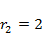 ,
, 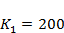 ,
, 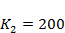 ,
, 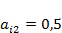 ,
, 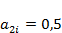 . Проанализировать зависимость судьбы популяций от соотношения значений их начальной численности
. Проанализировать зависимость судьбы популяций от соотношения значений их начальной численности 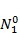 ,
, 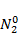 .
.
Практическое задание №5. Компьютерное моделирование трудноформализуемых объектов (финансовые, экономические, социальные процессы)
Выберите модель финансового, экономического или социального процессов (вар. 1-7 финансовый, вар. 8-15 экономический, вар. 16-22 социальный процессы). Проведите ее полное исследование и численную реализацию. Проанализируйте результаты моделирования. Подготовьте отчет.
МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ ПО ВЫПОЛНЕНИЮ ПРАКТИЧЕСКИХ ЗАДАНИЙ
1. При проведении расчетов необходим контроль точности результатов и устойчивости применяемого численного метода. Для этого достаточно ограничиться эмпирическими приемами (например, сопоставлением решений, полученных с несколькими разными шагами по времени).
2. Целесообразно применять для моделирования стандартные методы интегрирования систем дифференциальных уравнений, описанные в математической литературе. Простейшие методы (метод Эйлера) часто бывают неустойчивы и их применение ведет к лишнему расходу времени.
3. Результаты моделирования следует выводить на экран компьютера в следующих видах: таблицы зависимостей численности популяций от времени, графики этих зависимостей. Уместны звуковые сигналы (одни – в критические моменты для моделируемого процесса, другие – через некоторый фиксированный отрезок пройденного пути и т.д.).
4. При выводе результатов в табличном виде следует учитывать, что соответствующий шаг по времени не имеет практически ничего общего с шагом интегрирования и определяется удобством и достаточной полнотой для восприятия результатов на экране. Экран, сплошь забитый числами, не поддается восприятию. Выводимые числа следует разумным образом форматировать, чтобы незначащие цифры практически отсутствовали.
5. При выводе результатов в графической форме графики должны быть построены так, как это принято в математической литературе (с указанием того, какие величины отложены по осям, масштабами и т.д.).
6. Поскольку таблицы и графики на одном экране обычно не помещаются, удобно сделать меню, в котором пользователь выбирает желаемый в настоящий момент вид представления результатов.
РОССИЙСКОЙ ФЕДЕРАЦИИ
Федеральное государственное автономное
образовательное учреждение высшего образования
«ЮЖНЫЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ»
 Кафедра интеллектуальных и
многопроцессорных систем Кафедра интеллектуальных и
многопроцессорных систем
| Т.В.Камышникова, А.В.Никитина, А.Е.Чистяков Непрерывные математические модели Учебно-методическое пособие для проведения практических работ |
 Таганрог
Таганрог
Издательство Южного федерального университета
2019
 |
УДК 517.949.8 (076.5)+
518.12 (076.5)
Никитина А.В., Кузнецова И.Ю.
Математические модели процессов и систем: учебно-методическое пособие. – Таганрог: Издательство ЮФУ, 2017. – 53 с.
Целью работы является обучение обучающихся работе с задачами, требующими большого объема вычислительной работы с использованием универсальных решающих программ типа MathCad.
Пособие предназначено для магистрантов всех специальностей, изучающих численные методы и современные проблемы прикладной математики и информатики.
Знаком * обозначены вопросы повышенной сложности.
Ил.: Библиогр.: назв.
Практическая работа №1. Прямые методы решения систем линейных алгебраических уравнений
Прямые методы теоретически позволяют за конечное число операций (действий) найти «точное» решение системы. Однако, в условиях вычислений на компьютерах, имеющих конечную разрядную сетку, прямые методы позволяют найти реально лишь приближенное решение системы, ввиду наличия погрешностей округления. Примерами прямых методов, рассматриваемых ниже, являются метод Гаусса и его модификации.
Дата: 2019-05-29, просмотров: 400.