Рассмотрим систему линейных алгебраических уравнений
 ,
| (1.1) |
где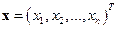 
– вектор неизвестных;
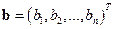– вектор свободных членов;
, 
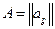– невырожденная матрица размерности 
.
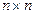В силу невырожденности матрицы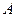 
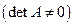для однородной системы уравнений с вектором правых частей 
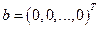имеем единственное тривиальное решение 
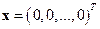. Для неоднородной системы имеем единственное решение 
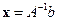, где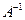 
– матрица, обратная .
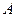Алгоритм метода исключения неизвестных был изобретен в 3 веке до нашей эры, хотя и носит имя Гаусса. Идея алгоритма состоит в приведении СЛАУ к эквивалентной ей системе с треугольной матрицей (прямой ход исключения), а затем к нахождению неизвестных последовательными подстановками (обратный ход). Данный метод требует числа арифметических операций порядка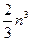 
. Он используется для решения СЛАУ с размерностью 
.
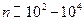Объединим матрицу 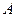и вектор 
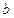в расширенную матрицу.
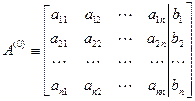
размерами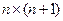 
, которая содержит всю известную информацию о системе (3.1).
Опишем вначале прямой ход, первый шаг которого состоит в обнулении всех элементов первого столбца матрицы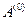 
, кроме того, что находится в первой строке.
Введем обозначение
.
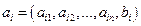C матрицей 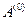можно обращаться так же, как с исходной системой (3.1), например, осуществлять элементарные преобразования. В качестве последних будем использовать перестановки строк, прибавление к элементам данной строки элементов какой-либо другой строки, умноженных на одно и то же число.
Найдем ненулевой элемент в первом столбце матрицы 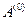. Такой элемент найдется всегда ибо, в противном случае, весь первый столбец состоит из нулей и матрица 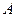– вырожденная. Пусть 
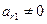, тогда поменяем местами строки номера 
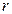и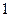 
. Если 
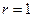, то, естественно, перестановка не требуется. Затем вычтем из каждой строки номера 
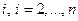первую строку, умноженную на число 
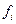, где
.
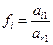В результате все элементы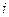 
-й строки изменят свои значения и станут равными
| (1.2) |
Здесь мы предполагаем, что хотя перестановка строк и могла состояться, однако нумерация элементов матрицы 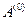осталась прежней. Введем обозначения
| (1.3) |
С учетом введенных обозначений (1.2) и (1.3) матрица 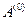преобразуется к матрице 
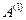и станет равной
 .
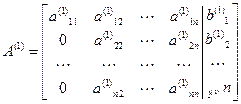| (1.4) |
Тот же алгоритм может быть применен на втором шаге к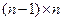 
матрице, которая получается из 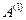, если убрать в ней первую строку и первый столбец. Применение этого алгоритма 
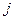раз приводит к матрице 
:
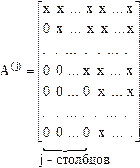
В матрице полученные нули располагаются в столбцах с номерами от 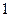до 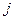ниже диагонали. Эти нули сохраняются во время следующих шагов алгоритма. В результате применения алгоритма 
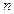раз система (3.1), в конечном счете, преобразуется в систему вида
 ,
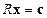| (1.5) |
где 
– верхняя (правая) треугольная матрица, т.е.
 .
| (1.6) |
Значения неизвестных можно вычислить из (3.6) по формулам
 ,
 .
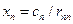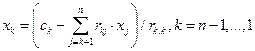| (1.7) |
Процесс приведения системы (1.1) к треугольному виду (1.6) называется прямым ходом, а нахождение неизвестных по формулам (1.7) называется обратным ходом.
Произведем подсчет числа арифметических операций в методе Гаусса. Число арифметических операций, необходимое для реализации прямого хода в методе Гаусса для решения систем уравнений порядка 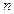, равно
 .
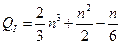| (1.8) |
При обратном ходе
 .
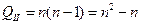| (1.9) |
Из формул (3.8) и (3.9) получаем оценку общего числа арифметических действий:
.
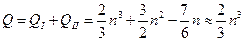Если имеется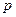 
систем вида (1.1) с одинаковыми матрицами 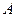и разными правыми частями 
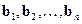,то целесообразно прямой ход осуществлять для всех систем одновременно, для чего следует вместо одной правой части, задаваемой вектором-столбцом, производить операции над 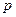правыми частями (матрицей порядка 
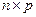). Количество арифметических операций, необходимое для реализации прямого метода Гаусса с учетом (1.8) и (1.9), есть
.
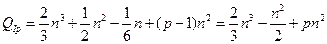Количество арифметических операций, необходимое для реализации 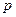обратных ходов (для 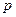систем) методом Гаусса, есть 
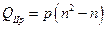. Откуда следует, что общее количество арифметических операций, необходимое для реализации систем с разными правыми частями, равно
.
Алгоритм LU-разложения
Данный алгоритм можно рассматривать как конкретную форму метода Гаусса. Алгоритм LU-разложения используется не только для решения СЛАУ, но и также для обращения матрицы, т.е. вычисления матрицы, обратной данной.
Пусть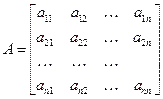 
и будем искать представление 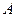в виде
 ,
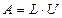| (1.10) |
где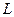 
и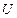 
– соответственно нижняя и верхняя треугольные матрицы вида
.
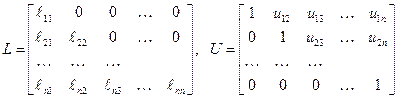Известно, что если все угловые миноры матрицы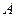 
отличны от нуля, т.е.
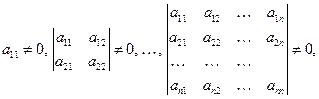
то разложение вида (1.10) существует и единственно. Для того чтобы получить расчётные формулы, поступим следующим образом. Обозначим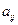 
произведение 
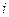-ой строки матрицы 
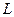на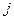 
-й столбец матрицы 
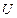, причём будем считать вначале , что 
.
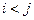Тогда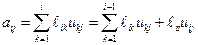 
.
Выразим из последней формулы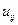 
:
 .
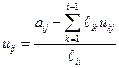| (1.11) |
Как это принято, будем считать в формуле (1.11) и далее, что сумма вида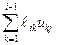 
равна нулю, если значение верхней границы индекса суммирования меньше нижней границы.
В случае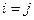 
имеем
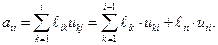
Учитывая, что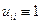 
, и выражая из последнего соотношения 
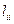, получаем:
 .
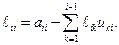| (1.12) |
Наконец, при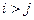 
получаем
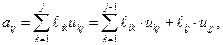
откуда, с учетом того, что 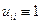, приходим к формуле
 .
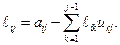| (1.13) |
Итак, расчетные формулы (1.11) – (1.13) получены. Для того чтобы при их применении не использовались неизвестные (не вычисленные) величины, необходимо выбрать соответствующий порядок вычисления элементов матриц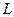 
и .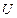
Например, можно рекомендовать порядок расчета элементов матриц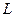 
и 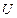, схематически изображенный на рис. 1.1. На нем цифры слева для матрицы 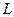и сверху – для матрицы 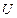означают, что на первом шаге рассчитывается 
по формуле (1.12), затем вычисляется элемент 
по формуле (1.11).
Далее (3 шаг) определяются элементы второй строки матрицы 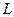в порядке, указанном стрелко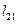й: 
и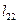 
(по формулам (1.13) и (1.12) соответственно).
На 4 шаге выполняется расчет элементов 3 столбца матрицы 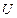в порядке, обозначенном стрелкой: 
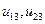(формулы (1.11)) и т.д.
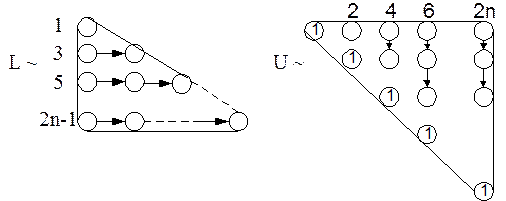
Рис. 1.1. Порядок расчета элементов матриц и
Рассмотрим теперь применение LU-разложения для решения СЛАУ вида
,
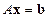где
.
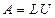Введем вспомогательный вектор 
:
 .
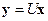| (1.14) |
Тогда исходную систему можно записать так
 .
| (1.15) |
В силу формул (1.14) и (1.15) решение исходной СЛАУ сводится к последовательному решению систем (1.15) и (1.14) соответственно с верхней и нижней треугольной матрицами.
Метод прогонки
Метод прогонки представляет собой вариант метода Гаусса, примененный к специальным системам линейных алгебраических уравнений и учитывающий ленточную структуру матрицы системы. Пусть имеем СЛАУ со специальной трехдиагональной формой матрицы:
| (1.16) |
или в матричной форме: 
, где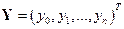 
– вектор неизвестных; 
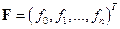– вектор правых частей; – квадратная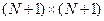 
матрица:
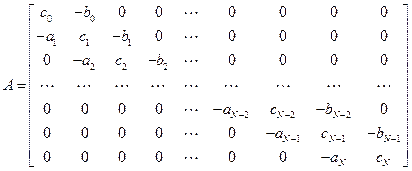
Системы вида (1.16) возникают при конечно-разностной аппроксимации краевых задач математической физики, описываемых обыкновенными дифференциальными уравнениями второго порядка с постоянными и переменными коэффициентами, а также уравнениями в частных производных. Ставится задача разработать экономичные методы решения задач вида (1.16), число арифметических операций для которых пропорционально числу неизвестных. Таким методом для системы (1.16) является метод прогонки. Специфика матрицы состоит в расположении ненулевых элементов, матрица 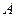– разреженная матрица, из 
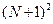элементов которой ненулевыми являются не более 
элементов. Это позволяет получить для решения СЛАУ простые расчетные формулы.
Будем искать решение (1.16) в виде
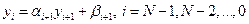
| (1.17) |
с неопределенными коэффициентами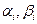 
. Выражение 
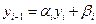подставим в (1.16):
,
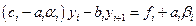c учетом (1.17) имеем
.
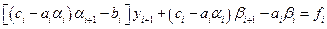Это равенство имеет место для любых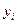 
, если
, 
.
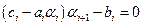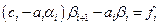Отсюда получаем рекуррентные формулы для определения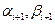 
:
 ;
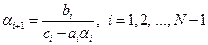| (1.18) |
 .
| (1.19) |
Коэффициенты 
, 
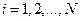называются прогоночными.
Если коэффициенты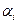 
и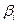 
известны, а также известно 
, то, двигаясь справа налево (от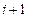 
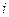к ) последовательно определяем все 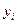. Задача нахождения по формулам (1.18), (1.19) решается слева направо (от 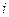к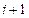 
). Начальные значения прогоночных коэффициентов 
можно определить следующим образом. Полагаем в формуле (1.17)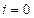 
, имеем 
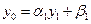, а из первого уравнения (3.16) 
, откуда
 .
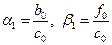| (1.20) |
Значение определяется следующим образом. Полагаем в формуле (1.17)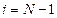 
, имеем 
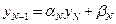, а из последнего уравнения (3.18) –
,
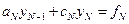откуда
 .
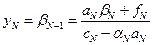| (1.21) |
Расчетные формулы (1.17) – (1.21) можно получить также из (1.16), если применить метод исключения Гаусса. Прямой ход метода заключается в том, что на первом шаге из всех уравнений системы (1.16) при помощи первого уравнения исключается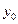 
, затем из преобразованных уравнений для 
при помощи уравнения, соответствующего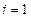 
, исключается 
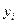и т.д. В результате получим одно уравнение относительно . На этом прямой ход метода прогонки заканчивается. На обратном ходе для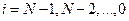 
находятся .
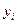Порядок счета в методе прогонки следующий:
1) исходя из значений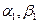 
, вычисленных по формулам (1.20), все остальные коэффициенты для 
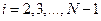определяются последовательно по формулам (1.18) и (1.19);
2) исходя из значения , рассчитанного по формуле (1.21), все остальные неизвестные 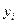, 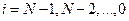определяются последовательно по формуле (1.17).
Изложенный метод поэтому называется правой прогонкой.
Аналогично выводятся формулы левой прогонки:
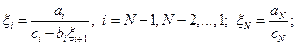
| (1.22) |
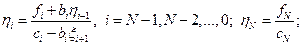
| (1.23) |
| yi+1 = xi+1yi + hi+1, i = N-1, N-2, …, 0; y0 = h0. | (1.24) |
Здесь 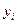находятся последовательно для значений 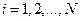; ход вычислений – слева направо.
В случае, если необходимо найти только одно неизвестное, например, 
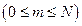или группу идущих подряд неизвестных, целесообразно комбинировать правую и левую прогонки. При этом получается метод встречных прогонок.
Произведем подсчет числа арифметических действий для метода правой прогонки. Анализ формул (1.17) – (1.21) показывает, что общее число арифметических операций есть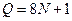 
. Коэффициенты 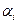не зависят от правой части СЛАУ (1.16) и определяются только элементами 
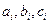матрицы 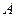. Поэтому, если требуется решить серию задач (1.16) с различными правыми частями, то прогоночные коэффициенты 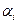вычисляются только для первой серии. Для каждой последующей серии задач определяются только коэффициенты 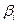и решение 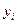, причем используются ранее найденные .
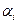На решение первой из серии задач расходуется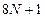 
операций, а на решение каждой следующей задачи – 
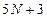операций. Число арифметических операций, необходимое для решения СЛАУ (1.16) методом левой прогонки и методом встречных прогонок, такое же, т.е. 
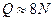. Метод правой прогонки будем называть корректным, если 
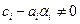при .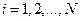
Решение 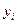находится по рекуррентной формуле (1.17). Эта формула может порождать накопление ошибок округления результатов арифметических операций. Пусть прогоночные коэффициенты 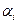и 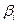найдены точно, а при вычислении допущена ошибка 
, т.е.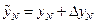 
. При вычислениях с помощью формулы (1.17) мы получаем
 .
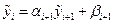| (1.25) |
Вычитая из (1.25) значение yi по формуле (1.17), имеем для погрешности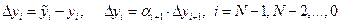 
с заданным . Отсюда ясно, что если 
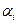по модулю больше единицы и если 
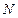достаточно велико, то вычисленное значение 
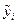будет значительно отличаться от искомого решения 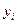. В этом случае говорят, что алгоритм прогонки неустойчив.
Определение. Алгоритм прогонки называется устойчивым, если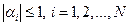 
.
Условия корректности и устойчивости алгоритма правой прогонки определяются следующей теоремой.
Теорема. Пусть коэффициенты системы (1.16) действительны и удовлетворяют условиям:
, 
, 
, 
, 
, 
, 
;
 , ;
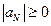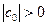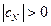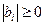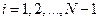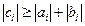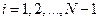| (1.26) |
 ,  ,
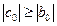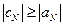| (1.27) |
причем хотя бы в одном из неравенств (1.26) и (1.27) выполняется строгое неравенство, т.е. матрица А имеет диагональное преобладание. Тогда для алгоритма (1.17) – (1.21) имеют место неравенства: ,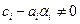 
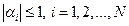, т.е. алгоритм метода правой прогонки корректен и устойчив.
Условия (1.26) и (1.27) теоремы обеспечивают также корректность и устойчивость алгоритмов левой и встречных прогонок. Эти условия сохраняются и для случая системы (1.16) с комплексными коэффициентами 
.
Легко показать, что при выполнении условий (1.26) – (1.27) теоремы система (1.16) имеет единственное решение при любой правой части.
Пример выполнения практической работы №1
Решите систему уравнений методом Гаусса и методом LU-разложения
Решите систему уравнений методом прогонки
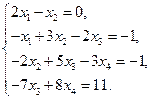
Дата: 2019-05-29, просмотров: 247.
