Для исследования сходимости итерационных методов, т.е. установления справедливости равенства 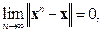 где
где 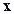 – точное решение системы (2.1), удобнее записывать эти методы в матричной, а не в координатной форме.
– точное решение системы (2.1), удобнее записывать эти методы в матричной, а не в координатной форме.
Представим матрицу 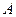 в виде суммы трех матриц
в виде суммы трех матриц
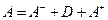 , где
, где
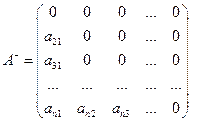 – строго нижняя треугольная часть матрицы
– строго нижняя треугольная часть матрицы 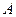 ,
,
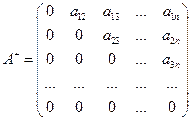 – строго верхняя треугольная часть матрицы
– строго верхняя треугольная часть матрицы 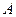 ,
,
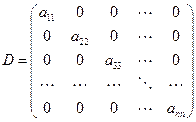 – диагональная часть матрицы А.
– диагональная часть матрицы А.
Очевидно, метод Якоби с использованием введенных обозначений в векторной форме принимает вид
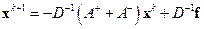 ,
,
где 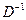 – матрица, обратная к матрице
– матрица, обратная к матрице 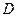 :
:
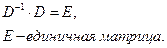
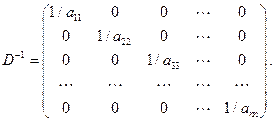
Метод Якоби также можно записать следующим образом:
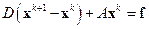 . .
| (2.7) |
Аналогичным образом из соотношений (2.6) можно получить представление метода Зейделя в векторной форме
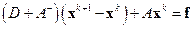 . .
| (2.8) |
Далее мы увидим, что векторные равенства (2.7) и (2.8) являются частными случаями так называемой канонической формы одношаговых (двухслойных) итерационных схем вида

| (2.9) |
где 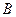 – квадратная невырожденная матрица размера
– квадратная невырожденная матрица размера 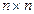 , называемая стабилизатором,
, называемая стабилизатором, 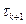 – число, называемое итерационным параметром.
– число, называемое итерационным параметром.
Матрица 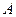 называется положительно определенной, если скалярное произведение
называется положительно определенной, если скалярное произведение 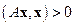 для всех ненулевых векторов
для всех ненулевых векторов 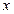 , или, что то же самое,
, или, что то же самое, 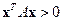 .
.
Сформулируем теорему, принадлежащую А.А. Самарскому.
Теорема. Пусть 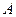 – симметричная положительно определенная матрица,
– симметричная положительно определенная матрица, 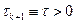 , и пусть выполнено неравенство для любого ненулевого вектора
, и пусть выполнено неравенство для любого ненулевого вектора 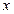 из
из 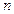 -мерного пространства.
-мерного пространства.
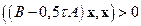 .
.
Тогда итерационный метод (2.9) сходится, т.е.
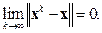
Покажем, как использовать данную теорему для доказательства сходимости, например, метода Зейделя.
Сравнивая (2.8) и (2.9), приходим к равенствам
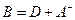 ,
, 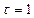 .
.
Таким образом, если 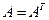 и
и 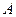 – положительно определенная матрица, то при условии выполнения неравенства
– положительно определенная матрица, то при условии выполнения неравенства 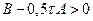 , что является краткой формой записи неравенства относительно скалярных произведений
, что является краткой формой записи неравенства относительно скалярных произведений
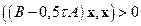 ,
, 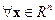 ,
,
метод Зейделя сходится.
Заметим, что
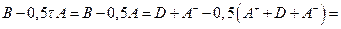
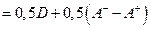 . .
| (2.10) |
Нетрудно проверить, что для любого 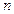 -мерного вектора
-мерного вектора 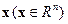
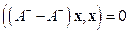 . .
| (2.11) |
C другой стороны, из неравенства 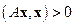
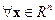 вытекает неравенство
вытекает неравенство
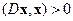 . .
| (2.12) |
В самом деле, выберем 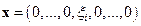 , где
, где 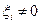 . Тогда
. Тогда
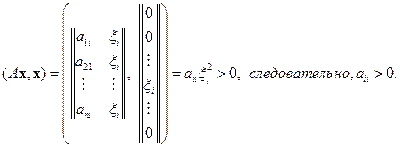
Поскольку 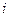 – любое, то все
– любое, то все 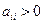 ,
, 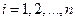 . Значит, справедливо неравенство (2.12). В силу (2.11) и (2.12) из (2.10) имеем
. Значит, справедливо неравенство (2.12). В силу (2.11) и (2.12) из (2.10) имеем
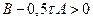 .
.
Вариационно-итерационные методы решения СЛАУ
Преимущество данных методов – они не используют никакой дополнительной информации об операторе 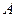 , т.е. значения
, т.е. значения 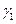 и
и 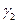 (собственные числа
(собственные числа 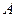 , входящие в оценку
, входящие в оценку 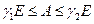 и необходимые для выбора
и необходимые для выбора 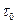 ) здесь не требуются. Рассмотрим методы минимальных невязок и скорейшего спуска.
) здесь не требуются. Рассмотрим методы минимальных невязок и скорейшего спуска.
Метод минимальных невязок
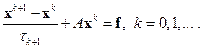
| (2.13) |
Для 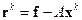 получим равенство, умножив обе части равенства (2.13) на матрицу
получим равенство, умножив обе части равенства (2.13) на матрицу 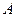 :
:
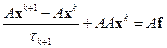 .
.
Меняя знаки и группируя слагаемые соответствующим образом, получаем:
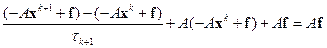 или
или
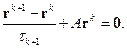
Параметр 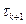 будем выбирать из условия минимума невязки
будем выбирать из условия минимума невязки 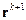 по норме
по норме
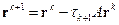 .
.
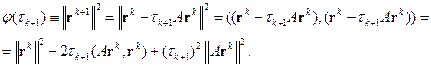
Продифференцируем 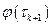 по
по 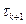 , получим
, получим
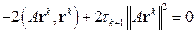 ,
,
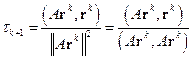 . .
| (2.14) |
Метод скорейшего спуска
Получается из условия минимума энергетической нормы погрешности 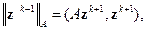 где
где 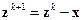 ,
, 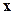 – точное решение исходной системы. Поскольку
– точное решение исходной системы. Поскольку 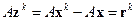 , и учитывая, что
, и учитывая, что
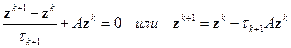 , получим
, получим
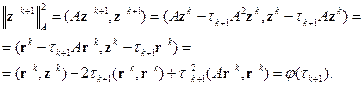
Дифференцируя 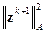 по
по 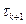 , получим
, получим
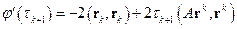 , откуда
, откуда
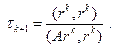
| (2.15) |
Пример выполнения практической работы №2
Решите систему уравнений методом Якоби, Зейделя, наименьших невязок и методом скорейшего спуска
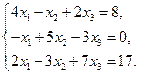
Дата: 2019-05-29, просмотров: 355.