Пусть проводится серия из 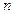 опытов. Результатами наблюдений являются численные значения  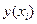некоторой величины. Поставим задачу: представить приближенным способом измеряемую величину  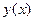в виде линейной комбинации известных (базисных) функций – 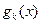, , 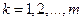, так, чтобы полученная зависимость согласовывалась с результатами наблюдений «наилучшим образом». Словосочетание «наилучшим образом» будет далее пояснено. 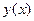Итак, будем искать зависимость  в виде

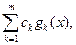
(3.13)

где коэффициенты  подлежат определению.

В общем случае в силу ошибок в измерениях при проведении опытов или «несовершенства» выбранной системы функций 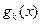, , 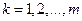возможно лишь выполнение приближенных равенств

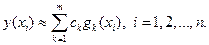
(3.14)

Сформируем разности между левыми и правыми частями равенств (3.14)

(3.15)

Очевидно, если бы удалось подобрать систему функций 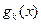 идеальным образом, а результаты измерений были бы точны, то вектор

,

называемый вектором невязки, состоял бы из нулевых элементов и его длина была бы минимально возможной (равной нулю).

Теперь мы можем уточнить, что следует понимать под приближением «наилучшим образом» зависимости 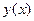 посредством линейной комбинации базисных функций 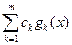. Будем требовать, чтобы длина вектора , которая вычисляется по формуле

,

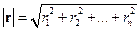(3.16)

была минимально возможной для данной системы функций 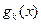, 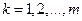. Мы можем «управлять» длиной вектора 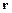, выбирая коэффициенты 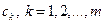. Далее вместо длины вектора  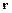нам удобнее будет пользоваться квадратом длины, который в соответствии с равенствами (3.15) и (3.16) есть

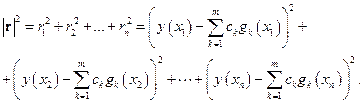
(3.17)

Ясно, что если 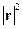 минимален, то и выбор коэффициентов 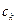,  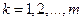наилучший в указанном выше смысле. Будем рассматривать правую часть равенства (3.17) как функцию  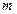переменных, в роли которых выступают коэффициенты , . Тогда необходимое условие экстремума функции  состоит в обращении в ноль частных производных, т.е.

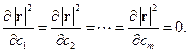
(3.18)

Дифференцируя правую часть формулы (3.17) по переменным 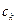, , 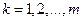как сложную функцию и приравнивая полученные частные производные нулю, приходим к равенствам:

,

,

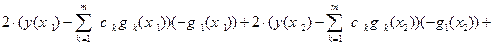
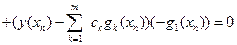        ¼        ¼         ¼        ¼        ¼        ¼     

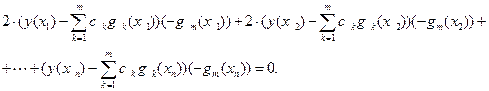
Сокращая на 2 обе части полученных равенств и записывая их в компактной форме, получаем систему

Раскрывая скобки и перенося известные величины в правые части, в итоге получаем систему, которая называется системой нормальных уравнений:

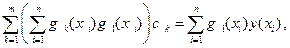
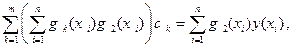
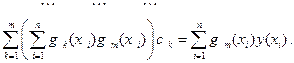
(3.19)

Заметим, что система (3.19) получена из необходимых условий экстремума функции 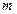 переменных. Можно доказать, что в точке 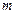-мерного пространства, которая является решением системы (3.19), выполняются достаточные условия наличия минимума функции 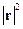, однако, ввиду громоздкости выкладок, мы этот вопрос здесь не рассматриваем.

Рассмотренный метод нахождения наилучшего в указанном смысле приближения к неизвестной функциональной зависимости , если задана система базисных функций 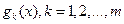, основанный на нахождении решения системы уравнений (3.19), называется методом наименьших квадратов.