Для получения однозначного ответа об уровне риска инвестиционного проекта на основе полученных данных необходимо ввести процедуру принятия решения. Такая процедура описана Смирновым А.П. в /17/.

Оператор оценивает входные данные с помощью субъективных качественных понятий типа “много”, ”мало” и т.п. Эти качественные оценки значений переменных u формализуются с помощью так называемых лингвистических переменных /11/.

Модель управления в рассматриваемом случае есть модель связи между входными переменными u и выходной переменной v. Механизм этой связи включает суждения оператора о значениях переменных. В результате на основе численного значения каждой из входных переменных оператор присваивает им качественные (нечеткие) значения. Свое решение он также принимает на основе нечеткого значения выходной переменной. Это означает, что оператор интуитивно пользуется нечеткой логикой, а конкретно – правилами нечеткого вывода.

Правила вначале формулируются с помощью термов (словесных описаний значений входных переменных). Каждое правило представляет собой текст, определяющий некоторое нечеткое отношение R между входными переменными u и выходной переменной v. Обозначим порядковый номер правила через L. 

Для превращения текста правила в формальную процедуру нужно установить вид правила композиционного вывода и форму нечеткой импликации.

В качестве правила композиционного вывода для рассматриваемого класса систем может быть принята максиминная композиция, а в качестве нечеткой импликации – правило минимума (пересечение нечетких множеств предпосылки и заключения). 

Нечеткое отношение R для L-го правила между j-й входной переменной u_j и выходной переменной v в соответствии с принятым правилом минимума выражено следующей функцией принадлежности

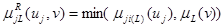                                                                                         (32)

Здесь индекс i(L) означает индекс i-го терма в L-м правиле вывода. Функция принадлежности (31) отображает отношение связи между числовыми значениями в паре (u_j, v). Чем больше ее значение, тем теснее эта связь.

Результаты измерения (наблюдения) входных переменных могут быть выражены как обычными числовыми (четкими) значениями, так и качественными или размытыми значениями (нечеткими числами).

Пусть входные переменные u_j представлены нечеткими числами f_j с функциями принадлежности m_fj (u_j). Заметим, что эти функции есть результат работы системы наблюдения (измерения) в отличие от ранее введенных функций m_ji(u_j), которые выражают мнение эксперта-оператора по поводу конкретных значений u_j. Тогда в соответствии с принятым правилом композиционного вывода можно записать связь между выходной переменной v и входной переменной u_j следующим образом

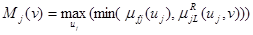                                                                                 (33)

Здесь M_j(v) есть функция принадлежности, устанавливающая локальную связь между нечеткой входной переменной u_j и нечеткой выходной переменной v.

Если система наблюдения дает конкретные числовые значения u_j=E_j, то формула (33) преобразуется к следующему виду

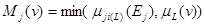                                                                                             (34)

Поскольку в L-м правиле логического вывода исходные посылки связаны логическим «и» (то есть наличием данных обо всех четырех входных переменных для вывода значения выходной переменной), то соответствующая операция над нечеткими множествами реализуется в виде их пересечения. Последнее же реализуется /18/ с помощью операции минимума над соответствующими функциями принадлежности. Обозначим нечеткое множество, соответствующее выходной переменной v и полученное на основании L-го правила вывода через Q_L, а его функцию принадлежности через m_QL(v). Тогда можно записать

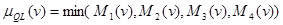                                                                          (35)

Данные о выходной переменной, полученные из всех правил вывода, должны быть логически объединены. Это соответствует операции максимума над функциями принадлежности /18/. Обозначив через Q результирующее нечеткое множество, соответствующее выходной переменной v, а через m_Q(v)- его функцию принадлежности, окончательно запишем

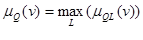                                                                                                             (36)

Теперь нужно оценить конкретное значение v^* для принятия решения о движении данной плавки. Эта процедура называется дефазификацией. Предложено использовать наиболее распространенный метод дефазификации /18/ – нахождение центра тяжести функции принадлежности

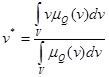                                                                                                                     (37)

Здесь V- область определения (универсальное множество) функции μ_Q(v).

Таким образом, полученная модель использует входные переменныe u_j, имеющие четкие значения, и выдает выходную переменную v также в четком виде., в то время как внутренняя структура модели является нечеткой.