Зададим набор нечетких чисел 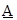= (a_min, 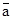, a_max) для анализа эффективности проекта (эти числа моделируют высказывание следующего вида: "параметр А приблизительно равен  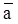и однозначно находится в диапазоне [a_min, a_max]".):

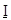-  = (I_min, 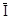, I_max) - инвестор не может точно оценить, каким объемом инвестиционных ресурсов он будет располагать на момент принятия решения;

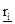-  = (r_{i min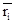}, , r_{i max}) - инвестор не может точно оценить стоимость капитала, используемого в проекте (например, соотношение собственных и заемных средств, а также процент по долгосрочным кредитам);

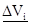-  = (V_min, 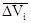, V_max) - инвестор прогнозирует диапазон изменения денежных результатов реализации проекта с учетом возможных колебаний цен на реализуемую продукцию, стоимости потребляемых ресурсов, условий налогообложения, влияния других факторов;

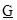-  = (G_min, 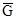, G_max) - инвестор нечетко представляет себе критерий, по которому проект может быть признан эффективным, или не до конца отдает себе отчет в том, что можно будет понимать под "эффективностью" на момент завершения инвестиционного процесса.

В том случае, если какой-либо из параметров 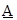 однозначно  задан, то нечеткое число  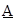вырождается в действительное число А с выполнением условия a_min =  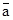= a_max. При этом существо метода остается неизменным.

Чтобы преобразовать формулу (4) к виду, пригодному для использования нечетких исходных данных, воспользуемся способом, предложенным автором в /6/.

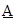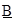Зададимся фиксированным уровнем принадлежности a и определим соответствующие ему интервалы достоверности по двум нечетким числам  и : [a₁, a₂] и [b₁, b₂], соответственно. Тогда основные операции с нечеткими числами сводятся к операциям с их интервалами достоверности. А операции с интервалами, в свою очередь, выражаются через операции с действительными числами - границами интервалов:

- операция "сложения"

[a₁, a₂] (+) [b₁, b₂] = [a₁ + b₁, a₂ + b₂],                                                                               (11)

- операция "вычитания"

[a₁, a₂] (-) [b₁, b₂] = [a₁ - b₂, a₂ - b₁],                                                                                  (12)

- операция "умножения"

[a₁, a₂] (´) [b₁, b₂] = [min(a₁b₁, a₁b₂, a₂b₁, a₂b₂ ), max(a₁b₁, a₁b₂, a₂b₁, a₂b₂ )],                        (13)

- операция "деления"

[a₁, a₂] (/) [b₁, b₂] = [a₁, a₂] (´) [1/b₂, 1/b₁]                                                                            (14)

- операция "возведения в степень"

[a₁, a₂] (^) i = [a₁ⁱ , a₂ⁱ].                                                                                                      (15)

По каждому нечеткому числу в структуре исходных данных получаем интервалы достоверности [I₁, I₂], [r_i1, r_i2], [DV_i1, DV_i2]. И тогда, для заданного уровня a, путем подстановки соответствующих границ интервалов в (4) по правилам (11) - (15), получаем

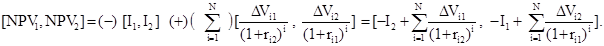    (16)

Далее, задавшись приемлемым уровнем дискретизации по a на интервале принадлежности [0, 1], автор в /6/ приводит функцию принадлежности результирующего нечеткого числа 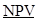 к треугольному виду, ограничиваясь расчетами по значимым точкам нечетких чисел исходных данных.

Далее, исходя из функций принадлежности и конкретизируя определенный уровень принадлежности a, автор строит зону неэффективных инвестиций и вычисляет площади ( 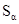) этой плоской фигуры в зависимости от интервальных значений чистой приведенной стоимости (NPV₁, NPV₂ ) и критерия эффекта (G₁, G₂).

После чего, предположив, что все реализации (NPV, G) при заданном уровне принадлежности a равновозможны, автор выводит степень риска неэффективности проекта j(a) через геометрическую вероятность события попадания точки (NPV, G) в зону неэффективных инвестиций

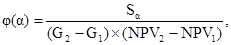                                                                                                                                                                                                                                                                                              (17)

Тогда итоговое значение степени риска неэффективности проекта он получает из уравнения 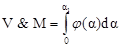(18) 

                                                                                                                  (18)

В /6/ он рассматривает частный случай, когда ограничение 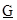определено четко уровнем G. С учетом формулы (18) и длинной цепи преобразований, автор получает меру оценки степени риска инвестиционных проектов, которая выглядит так

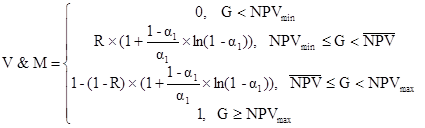                                                       ,                                                                                                                                                          (19)

где

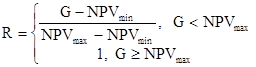,                                                                                (20)

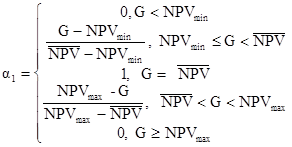                                                                        (21)

Таким образом, степень риска V&M принимает значения от нуля до единицы. Каждый инвестор, исходя из своих инвестиционных предпочтений, может классифицировать значения V&M, выделив для себя отрезок неприемлемых значений риска.

В /15/ автор рассматривает полученную оценку степени риска для различных способов представлений чистого приведенного эффекта.

Результат для случая, когда критерий G представлен нечетким числом произвольного вида, представлен автором в /16/.

В работе В.В.Каблукова /2/ рассмотрена оценка риска, на основе вероятностного подхода. Риск оценивается при помощи системы критериев: критерия неопределенности, ликвидности и покрытия. Критерий неопределенности представляет собой дисперсию значений чистого приведенного эффекта. Для его расчета необходим довольно большой объем информации о входных данных, включающий в себя и распределение вероятностей, и информацию о корреляционной зависимости. Распределение задается, исходя из предположений экспертов, и несет в себе большую долю субъективизма, а для получения информации о корреляционной зависимости требует трудоемких дополнительных исследований. Выходными данными этой модели являются три критерия, значения которых необходимо сравнить между собой для получения ответа на вопрос об общем уровне риска проекта.

Метод оценки риска, разработанный Недосекиным А.О. /6/, опирается на теорию нечетких множеств. Все данные представлены нечеткими числами, а риск рассматривается как вероятность попадания значения чистого приведенного эффекта в зону неэффективных инвестиций. Чем больше эта вероятность тем, соответственно, больше риск. Это действительно так, но оценка риска может получиться односторонней, если в процессе инвестирования не учитывать во сколько раз значение заемных средств превышает собственные, а также проводить сопоставления полученных в ходе реализации проекта результаты с прогнозными.

 Разработка модели, учитывающей все недостатки данных методов, является целью этой работы. Необходимо создать модель оценки уровня риска проекта, которая не опиралась бы на характер распределений входных данных, их зависимость друг от друга и учитывала бы неопределенность с различных сторон. Помимо этого модель должна давать однозначный ответ о уровне риска проекта вне зависимости от того сколько в нее входит критериев оценки.

Специальная часть