В предложенной модели в качестве критерия для учета неопределенности (риска) стратегического инвестиционного проекта было выбрано среднеквадратическое отклонение чистого приведенного эффекта (NPV) от его математического ожидания. Если по результатам расчетов будет выявлено, что дисперсия достаточно большая, то риск того, что ожидаемое значение NPV примет запланированное значение, будет также достаточно большим.
Понятие дисперсии, так же как и математического ожидания, функции распределения и ковариации не определено для нечетких чисел, поэтому использование формулы (22) вызывает определенные трудности. В результате для учета риска была рассмотрена разработанная Недосекиным А.О. оценка возможности того, что по результатам инвестиционного процесса значение NPV окажется ниже предустановленного граничного уровня /6/. Таким образом, первый критерий оценки риска проекта будет вычисляться по следующей формуле
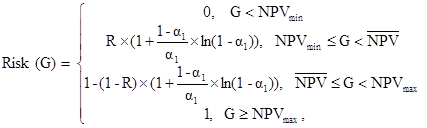(27)
где
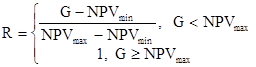, (28)
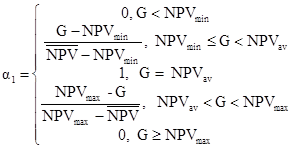. (29)
где Risk(G) – вероятность того, что значение чистого приведенного эффекта окажется ниже предустановленного граничного уровня, доли единицы,
G – уровень эффективности проекта, денежные единицы,
NPVmin – минимальное значение чистого приведенного эффекта из заданного диапазона, денежные единицы,
NPVmах – максимальное значение чистого приведенного эффекта из заданного диапазона, денежные единицы,
NPVav – среднее значение чистого приведенного эффекта из заданного диапазона, денежные единицы,
α1 – функция принадлежности нечеткого числа NPV, доли единицы.
Степень риска Risk(G) принимает значение от 0 до 1. Каждый инвестор, исходя из своих инвестиционных предпочтений, может классифицировать значение Risk(G), выделив для себя отрезок неприемлемых значений риска. Возможна также более подробная градация степени риска, которая будет рассмотрена позже.
Формула для оценки ликвидности стратегического инвестиционного проекта, в силу введения нечетких чисел в модель и описанных в литературном обзоре операций, примет следующий вид
 |
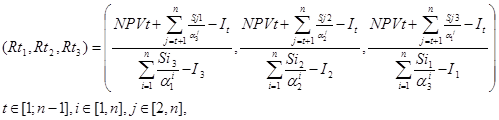(30)
где Rt1– минимальное значение коэффициента ликвидности в момент времени t, доли единицы,
Rt2– среднее (наиболее ожидаемое) значение коэффициента ликвидности в момент времени t, доли единицы,
Rt3– максимальное значение коэффициента ликвидности в момент времени t, доли единицы,
Si1– минимальное значение чистого денежного потока в i-й планово-учетный период, денежные единицы,
Si2– среднее значение чистого денежного потока в i-й планово-учетный период, денежные единицы,
Si3– максимальное значение чистого денежного потока в i-й планово-учетный период, денежные единицы,
a1 – минимальное значение безрисковой ставки дисконтирования, доли единицы,
a2 – среднее значение безрисковой ставки дисконтирования, доли единицы,
a3 – максимальное значение безрисковой ставки дисконтирования, доли единицы,
n – число планово-учетных периодов проекта,
I – номер планово-учетных периодов,
j – номер планово-учетного периода на момент реализации стратегического инвестиционного проекта,
NPVt - фактически полученная стоимость стратегического инвестиционного проекта (денежные потоки, полученные на момент времени t), денежные единицы,
I1 –минимальное значение первоначальных капиталовложений, денежные единицы,
I2 – максимальное значение первоначальных капиталовложений, денежные единицы,
I3 – среднее значение первоначальных капиталовложений, денежные единицы.
Критерий покрытия в рамках данной модели оценивается по следующей формуле:
 |
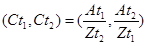(31)
где Сt1 – минимальное значение критерия покрытия в момент времени t, доли единицы,
Сt2 – максимальное значение критерия покрытия в момент времени t, доли единицы,
Аt1 - минимальное значение собственного капитала субъекта в момент времени t, денежные единицы,
Аt2 - максимальное значение собственного капитала субъекта в момент времени t, денежные единицы,
Zt1 - минимальное значение заемного капитала в момент времени t, денежные единицы,
Zt2 - максимальное значение заемного капитала в момент времени t, денежные единицы.
Дата: 2019-05-29, просмотров: 243.
