В соответствии с полученным типом данных и поставленной целью исследования должна быть проведена статистическая обработка и анализ эмпирических данных. Результаты диагностики с помощью разных методик дают нам данные в разных шкалах измерения. Это важно помнить, так как от типа измерения зависит способ статистической обработки данных.
«Номинативная шкала», которую можно перевести как «шкала названий», встречается в опросниках и тестах, дающих нам в результате диагностики каждого испытуемого, что он принадлежит к какому-либо типу (типу темперамента, личности, акцентуации, типу поведения в конфликтных ситуациях, типу семейных отношений или детско-родительских отношений и т.п.) Представление таких данных возможно в виде частотного распределения типов в выборке или подвыборках (частота распределения представляется в виде процентов или количестве испытуемых, относящихся к разным типам). Выявление взаимосвязей между показателями, измеренными в номинативных шкалах (например, связан ли тип темперамента и тип поведения в конфликтных ситуациях) требует составления таблиц сопряженности (при данном примере – будет таблица многоклеточной сопряженности). Это таблицы, в которых отражены частоты совпадения типов двух измеренных переменных (в данном примере – четырех типов темперамента и пяти типов поведения в конфликтных ситуациях). Часто по такой таблице сразу можно увидеть, связаны ли между собой те или иные типы или связи не наблюдается. Свои выводы исследователь проверяет на статистическую достоверность с помощью критерия хи-квадрат (способ расчета приведен в специальной литературе) и вычисляет силу связи с помощью соответствующего коэффициента сопряженности. Если необходимо при данных такого типа сопоставить две выборки, и статистически подтвердить, что в одной из них частота встречаемости данного типа меньше, чем в другой, то можно применить либо критерий хи-квадрат (если частота представлена в количестве испытуемых (случев)) или критерий углового преобразования Фишера (если частота представлена в виде процентов).
«Ранговая шкала» - когда измеренные переменные представлены в порядке в возрастания или убывания их значимости, или из выраженности. Такие данные мы получаем в классическом варианте теста Рокича на ценностные ориентации, в некоторых методиках измерения самооценки, мотивов. В этом случае исследователь получает ряд индивидуальных иерархий ценностей (представлений или мотивов). Для обобщения данных в группах нужно, прежде всего, выяснить, насколько индивидуальные системы представлений совпадают между собой или же они настолько разные, что их нельзя описывать как некую общность. Для этого используется коэффициент конкордации. Если выясняется, что индивидуальные системы представлений, в целом, близки, то можно описывать систему ценностных представлений данной выборки в целом, опираясь на средние ранги ценностей. Если выясняется, что в данной выборке нет единства в мнениях, то можно выявить типы ценностных представлений в данной группе, применив кластерный анализ. Выявленные типы можно описывать и сопоставлять с другими данными. Сходство-различие ценностных представлений разных групп испытуемых можно определить с помощью коэффициента ранговой корреляции Спирмена.
«Интервальная шкала» - когда переменные измерены по уровню их индивидуальной выраженности в баллах (например, уровень тревожности, эмпатии, агрессивности, самоактуализации, маскулинности, фемининности и т.п.) Можно утверждать, что большинство методик в психологии использует измерение в интервальных шкалах. Интервальные шкалы позволяют (при соблюдении определенных правил, конечно) для сопоставления двух выборок (сходство-различие по данному показателю) применять t -критерий Стьюдента, а для установления взаимосвязей между двумя и более показателями – коэффициент линейной корреляции Пирсона.
В психологических исследованиях невозможно учесть все возможные влияния на элементы выборки, поэтому оценка параметров генеральной совокупности, сделанная на основании выборочных данных, как указывает О.Ю.Ермолаев, всегда будет сопровождаться погрешностью, и поэтому подобного рода оценки должны рассматриваться как предположительные, а не как окончательные утверждения. Такие предположения о свойствах и параметрах генеральной совокупности получили название статистических гипотез.
При проверки статистических гипотез используются два понятия: нулевая гипотеза и альтернативная гипотеза. Нулевая гипотеза (обозначение Ho) – это гипотеза о сходстве, альтернативная гипотеза (обозначение H1) – это гипотеза о различии.
Уровень статистической значимости результата исследования (p-уровень) – это количественно выраженная вероятность, свидетельствующая о том, что результаты достоверны. Уровнем значимости называется вероятность ошибочного отклонения нулевой гипотезы.
В психологии считается, что низшим уровнем статистической значимости является уровень p=0,10; достаточным – p=0,05; высшим – p=0,01.
Используя методы математической статистики, исследователь получает так называемую эмпирическую статистику (Кэмп. – коэффициент эмп.). Кэмп – это условное название. Полученную эмпирическую статистику необходимо сравнить с двумя критическими величинами, которые соответствуют рассмотренным выше уровням статистической значимости. Критические величины для используемых коэффициентов находятся в специальных таблицах.
Для принятия статистического решения выделяют следующие этапы.
1) Формулировка нулевой и альтернативной гипотез.
2) Определение объема выборки N.
3) Выбор соответствующего уровня значимости или вероятности отклонения нулевой гипотезы. Это может быть величина меньшая или равная 0,05 (5% уровень значимости). В зависимости от важности исследования можно выбрать уровень значимости в 0,1% или даже в 0,01%.
4) Выбор статистического метода, который зависит от типа решаемой психологической задачи.
5) Вычисление соответствующего эмпирического значения по экспериментальным данным, согласно выбранному статистическому методу.
6) Нахождение по таблице для выбранного статистического метода критических значений, соответствующих уровню значимости для Р=0,05 и для Р=0,01.
7) Построение оси значимости и нанесение на нее табличных критических значений и эмпирического значения. Для этого целесообразно пользоваться каждый раз приведенными выше рисунками.
8) Формулировка принятия решения.
Е.В.Сидоренко и О.Ю.Ермолаев предложили следующую классификацию задач и методов их решения (таблица 1):
Таблица 1
| Задачи | Условия | Методы |
| 1. Выявление различий в уровне исследуемого признака | a) Две выборки испытуемых | Критерий Макнамары Q критерий Розенбаума U критерий Манна-Уитни φ - критерий (угловое преобразование Фишера) |
| b) Три и больше выборок испытуемых | S критерий Джонкира H критерий Крускала-Уоллиса | |
| Задачи | Условия | Методы |
| 2. Оценка сдвига значений исследуемого признака | a) Два замера на одной и той же выборке испытуемых | T критерий Вилкоксона G критерий знаков φ критерий (угловое преобразование Фишера) t –критерий Стьюдента |
| b) Три и более замеров на одной и той же выборке испытуемых | 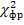 критерий Фридмана
L критерий тенденций Пейджа
t –критерий Стьюдента критерий Фридмана
L критерий тенденций Пейджа
t –критерий Стьюдента
| |
| 3. Выявление различий в распределении признака | a) При сопоставлении эмпирического распределения с теоретическим | χ2 критерий Пирсона λ критерий Колмогорова - Смирнова t –критерий Стьюдента |
| b) При сопоставлении двух эмпирических распределений | χ2 критерий Пирсона λ критерий Колмогорова - Смирнова φ критерий (угловое преобразование Фишера) | |
| 4. Выявление степени согласованности изменений | a) Двух признаков | φ коэффициент корреляции Пирсона η корреляционное отношение Пирсона τ коэффициент корреляции Кендела ρ коэффициент ранговой корреляции Спирмена |
В обработке массива данных приветствуются многомерные методы, такие, как интеркорреляционные матрицы и плеяды, кластерный или факторный анализ. Но, в любом случае, статистическая обработка является не самоцелью, выбор метода должен определяться целью исследования.
Кластерный и факторный анализы предназначены для перехода от исходной совокупности множества переменных (или объектов) к существенно меньшему числу факторов (кластеров).
Основные отличия факторного и кластерного анализа:
1) Целью факторного анализа является замена большого числа исходных переменных меньшим числом факторов. Кластерный анализ применяется для того, чтобы уменьшить число объектов путем их группировки. Кластерный анализ исходит из сходства объектов по измеренным признакам.
2) Кластерный анализ может выступать как более простой аналог факторного анализа.
3) Действия, выполняемые в ходе статистических операций в каждом из вариантов анализа, различаются.
Факторный анализ применяется для уменьшения большого числа изучаемых переменных до некоторого набора признаков. В образующихся группах прослеживается связь фактора с входящими в него переменными. Данный вид анализа позволяет оптимально минимизировать размерность исходных данных, но не их содержание.
В основе факторного анализа лежит процедура корреляционного анализа, когда строится корреляционная матрица для всех изучаемых переменных. Необходимость подвергать полученные взаимосвязи факторизации возникает при наличии слишком большого множества признаков в связи с тем, что введение факторов упрощает структуру явления.
Фактор – это латентная причина, обуславливающая объединение признаков в одну группу. Соответственно, задачами факторного анализа являются:
1) Исследование структуры взаимосвязи переменных;
2) Идентификация факторов как скрытых переменных – причин взаимосвязи исходных переменных;
3) Сокращение количества признаков с минимальными потерями исходной информации.
Этапы факторного анализа:
1. Выбор и подготовка исходных данных для факторного анализа. Для дальнейшей факторизации признаков исходные эмпирические данные необходимо разместить в правильной последовательной форме. Сводный протокол должен иметь следующий вид: столбцы – признаки, строки – испытуемые.
2. Определение исследователем количества факторов. Заранее заданное число факторов влияет на результаты факторного анализа. Для этого обычно применяют анализ главных компонент и используют график собственных значений (screen plot). Количество факторов определяется приблизительно по точке перегиба на графике. Исследователь может варьировать число факторов до получения оптимальной для интерпретации картины.
3. Определение метода вращения факторов. Одним из наиболее часто используемых методов факторного анализа является метод варимакса, который обеспечивает минимизацию количества показателей, связанных с каждых из выделенных факторов. В каждый фактор группируются только показатели, которые в большей степени с ним связаны.
4. Факторизация матрицы интерпретаций. Результатом варимакс вращения является таблица факторов и факторных нагрузок. Изначально заданное количество факторов на втором этапе определяет количество столбцов таблицы. Строки содержат информацию о признаках и факторных нагрузок. Факторные нагрузки – корреляции переменных с выделенным фактором. Чем больше величина факторной нагрузки, тем сильнее связь этой переменной с фактором, то есть факторная нагрузка (степень взаимосвязи) показывает, насколько данная переменная обусловлена действием соответствующего фактора. Обозначение фактора вводится на основе содержания самых весомых признаков, входящих в него, то есть обладающих максимальной факторной нагрузкой. Переменные с минимальной факторной нагрузкой по всем факторам исключаются из дальнейшего анализа и не учитываются при интерпретации.
5. Составление нового сводного протокола исходных данных. Вычисляются значения выделенных факторов для каждого испытуемого, результаты представляются в графической форме. График факторов представляет собой пересечение двух прямых (фактор 1, фактор 2). На графике отмечается точка, являющаяся соотношением исходных значений по двум выделенным факторам.
6. Интерпретация факторов. Интерпретация факторов осуществляется на основе анализа факторных нагрузок. По каждому столбцу (фактору) выделяются переменные с доминирующими факторными нагрузками. Именно эти переменные определяют содержание фактора. Факторные нагрузки могут быть представлены как отрицательными, так и положительными коэффициентами корреляции. Отрицательный знак переменной указывает на её противоположный полюс. Соответственно, после анализа названия переменных с учетом их факторных нагрузок определяется название самого фактора.
Дата: 2019-05-29, просмотров: 361.