1. Комбинации, состоящие из k элементов, взятых из п различных элементов, и отличающиеся порядком следования элементов, называются…
1). Сочетаниями 2). Перестановками
3). Размещениями 4). Переборами
2. Значение выражения 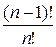 равно…
равно…
1)  2)
2)  3)
3) 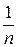 4) п
4) п
3. Относительной частотой случайного события 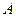 называется величина, равная:
называется величина, равная:
1). Отношению числа случаев, благоприятствующих событию  к общему числу равновозможных, несовместных событий;
к общему числу равновозможных, несовместных событий;
2). Пределу, к которому стремится отношение числа случаев, в которых реализуется событие  , к общему числу испытаний при неограниченном увеличении числа испытаний;
, к общему числу испытаний при неограниченном увеличении числа испытаний;
3). Отношению числа случаев, в которых реализуется событие 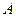 , к общему числу испытаний;
, к общему числу испытаний;
4).Отношению общего числа испытаний к числу испытаний, в которых реализуется событие А.
4. Укажите диапазон значений, которые может принимать вероятность случайного события 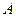 :
:
1). 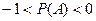 2).
2). 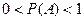 3).
3).  4).
4). 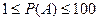
5. В урне находится 6 черных и 4 белых шара. Определите вероятность одновременного вынимания двух белых шаров.
1) 4/6 2) 0,2 3) 0,13 4) 0,8
6. Три стрелка стреляют по мишени. События: А – первый стрелок попал в мишень, В – второй стрелок попал в мишень, С – третий стрелок попал в мишень являются…
1). Несовместными и независимыми 2). Совместными и независимыми
3). Несовместными и зависимыми 4). Совместными и зависимыми
7. Вероятность события есть число, принадлежащее промежутку…
1).  2).
2). 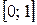 3).
3). 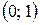 4).
4). 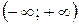
8. Вероятность того, что дом может сгореть в течение года, равна 0,0001. Застраховано 500 домов. Для вычисления вероятности того, что за год сгорит 5 домов, следует использовать…
1). Локальную формулу Лапласа 2). Интегральную формулу Лапласа
3). Формулу Пуассона 4). Формулу Бернулли.
РАЗДЕЛ II . СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
Глава 5. Дискретная случайная величина
Основные понятия случайных величин
Определение. Случайной называется величина, которая в результате испытания принимает одно и только одно возможное значение, какое именно заранее неизвестно.
Случайные величины делятся на дискретные и непрерывные.
Определение. Случайная величина называется дискретной, если в результате испытания она принимает одно из значений х1, х2, х3, … , х n, … с соответствующей вероятностью р1, р2, … , р n, …
Определение. Непрерывной называется случайная величина, которая может принимать любое значение из некоторого промежутка.
Например, число студентов на лекции – дискретная случайная величина, продолжительность лекции – непрерывная.
Закон распределения дискретной случайной величины
Соответствие между возможными значениями х k случайной величины Х и их вероятностями р k называется законом распределения вероятностей дискретной случайной величины Х.
Закон распределения обычно задается таблицей:
| Возможные значения случайной величины Х | х1 | х2 | … | хn |
| Вероятности этих значений Р | р1 | р2 | … | рn |
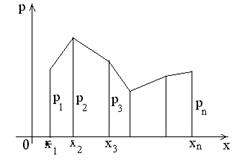
То, что случайная величина Х принимает одно из значений х1, х2, … , х n, есть достоверное событие и поэтому должно выполняться равенство 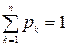 (в случае бесконечной последовательности значений
(в случае бесконечной последовательности значений 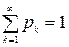 ).
).
Закон распределения может быть задан графически в виде многоугольника распределения вероятностей, т.е. в виде ломаной, соединяющей точки (х k, р k).
Примеры.
1. Переменная величина Х есть число очков, выпадающее на верхней грани игральной кости при ее однократном бросании. Составить закон распределения этой случайной величины.
Решение.
Так как любое число очков при однократном бросании кости выпадает с вероятностью 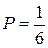 , то закон распределения случайной величины имеет вид:
, то закон распределения случайной величины имеет вид:
| Х | 1 | 2 | 3 | 4 | 5 | 6 |
| р | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 |
2. Вероятность попадания при каждом выстреле р=0,8. Имеется три снаряда. Определить вероятность того, что будет израсходован один снаряд, два снаряда, три снаряда, если стрельба ведется до первого попадания или промаха всеми тремя снарядами. Составить таблицу распределения случайной величины Х – числа израсходованных снарядов.
Решение.
Пусть Х – число израсходованных снарядов. Обозначим  - вероятность того, что будет израсходовано х k снарядов.
- вероятность того, что будет израсходовано х k снарядов.
Тогда Р(х=1)=0,8, Р(х=2)=(1-р)р=0,16, Р(х=3)=(1-р)2=0,04.
Таблица распределения будет иметь вид
| Х | 1 | 2 | 3 |
| р | 0,8 | 0,16 | 0,04 |
3. Экзаменатор задал студенту 4 дополнительных вопроса. Вероятность того, что студент ответит на любой заданный вопрос 0,9. Составить закон распределения случайной величины Х – числа ответов на заданные вопросы.
Решение.
Используем формулу Бернулли  . Здесь n=4, р=0,9, q=0,1.
. Здесь n=4, р=0,9, q=0,1.
 ,
,
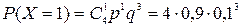 ,
,
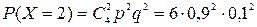 ,
,
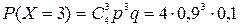 ,
,
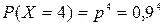 .
.
| Х | 0 | 1 | 2 | 3 | 4 |
| Р | 0,0001 | 0,0036 | 0,0486 | 0,2916 | 0,6561 |
Дата: 2019-05-28, просмотров: 436.