Локальная теорема Муавра-Лапласа. Если вероятность р наступления события А в каждом испытании постоянна и отлична от 0 и 1, то вероятность 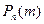 того, что событие А произойдет m раз в n независимых испытаниях при достаточно большом числе n, приближенно равна
того, что событие А произойдет m раз в n независимых испытаниях при достаточно большом числе n, приближенно равна 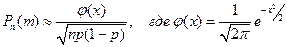 - локальная функция Лапласа и
- локальная функция Лапласа и 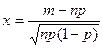 .
.
Все значения функции 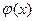 приведены в таблице (приложение 1). Локальная функция Лапласа является четной функцией т.е.
приведены в таблице (приложение 1). Локальная функция Лапласа является четной функцией т.е. 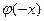 =
=  .
.
При х > 4 локальная функция Лапласа φ(х) =0.
Применяется теорема Лапласа при n больших 10. Чем больше n, тем точнее приближенная формула.
Интегральная теорема Муавра-Лапласа: Если вероятность наступления события А в каждом испытании постоянна и равна р 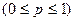 , а число n достаточно велико, то вероятность Pn ( m 1
, а число n достаточно велико, то вероятность Pn ( m 1  m
m  m 2 ) того, что событие А появится в n независимых испытаниях от m 1 до m 2 раз приближенно равна:
m 2 ) того, что событие А появится в n независимых испытаниях от m 1 до m 2 раз приближенно равна:
Pn(m1 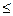 m
m 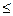 m 2) = Ф(х²) – Ф(х¢)
m 2) = Ф(х²) – Ф(х¢)
где Ф(х) = 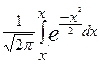 интегральная функция Лапласа, и
интегральная функция Лапласа, и
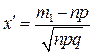 ;
; 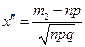 .
.
При решении задач, требующих применение интегральной теоремы Лапласа, пользуются специальными таблицами (приложение 2).
Для значений х>5 полагают Ф(х)=0,5.
Для отрицательных значений х, пользуются этой же таблицей, учитывая, что интегральная функция Лапласа нечетная, т.е. Ф(-х)= -Ф(х).
Примеры.
1. Вероятность получения с конвейера изделий первого сорта равна 0,9. Определить вероятность того, что из взятых на проверку 600 изделий 530 будут первого сорта.
Решение:
n =600, m =530, р=0,9, q=1-0,9=0,1 Вычислим значение х:
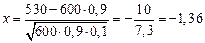
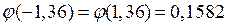
Р600(530)= 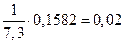
2. Вероятность того что деталь не прошла проверку равна 0,2. Найти вероятность того что среди 400 случайно отобранных деталей окажется непроверенных больше 100 деталей.
Решение:
n=400, m1=100, m2=400 p=0,2, q=0,8.
х¢ =  х² =
х² = 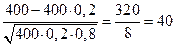
Ф(х¢)= 0,4938, Ф(х²)=0,5 Р(100 £m£ 400)=0,4938+0,5=0,9938
Формула Пуассона
При большом числе испытаний n и малой вероятности р формулой Бернулли пользоваться неудобно, например, 0,951000 вычислить трудно. В этом случае для вычисления вероятности того, что в n испытаниях (n – велико) событие произойдет m раз используют формулу Пуассона
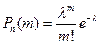 ,
,
где λ=np=const – среднее число появлений события в n испытаниях.
Примеры.
1. Устройство состоит из 1000 элементов, работающих независимо один от другого. Вероятность отказа любого элемента в течении времени Т равна 0,002. Найти вероятность того, что за время Т откажут ровно три элемента.
Решение:
n=1000, p=0,002, λ=np=2, m=3.
Искомая вероятность 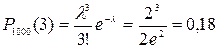 .
.
2. Завод отправил на базу 500 изделий. Вероятность повреждения изделия в пути 0,004. Найти вероятность того, что в пути повреждено меньше трех изделий.
Решение:
n=500, p=0,004, λ=2.
По теореме сложения вероятностей
 .
.
3. Магазин получил 1000 бутылок минеральной воды. Вероятность того, что при перевозке бутылка окажется разбитой, равна 0,003. Найти вероятность того, что магазин получит более двух разбитых бутылок.
Решение:
По формуле Пуассона:
λ=np=1000·0,003=3
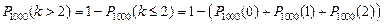

Примеры решения типовых задач
1. В жилом доме имеется 6400 ламп, вероятность включения каждой из них в вечернее время равна 0,5. Найти вероятность того, что число одновременно включенных ламп будет между 3120 и 3200.
Решение:
Используем интегральную теорему Лапласа, где n = 6400, p = 0,5, q = 1-p = 0,5, m1 =3120, m2 = 3200.
 .
.
 ;
;  .
.
Находим по таблице приложения 2:

Тогда 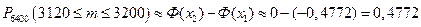 .
.
2. Вычислительное устройство состоит из 1000 элементов, работающих независимо друг от друга. Вероятность отказа каждого элемента за смену равна 0,024. Найти вероятность, что за смену откажут 6 элементов.
Решение:
Используем локальную теорему Лапласа:
n =1000, m =6, р=0,024, q=1-0,024=0,976.
Вычислим значение х:

Найдем по таблице приложения 1:

Р1000(6)= 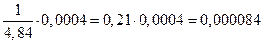
3. Найти вероятность того, что если бросить монету 200 раз, то орел выпадет от 90 до 110 раз.
Решение:
Так как число n=200 достаточно велико, будем использовать интегральную теорему Лапласа для подсчета вероятности, где m1 =90, m2 = 110, вероятность появления орла равна р = 0,5, и не появления q=0,5.
 . .
 . .  .
Находим по таблице приложения 2: .
Находим по таблице приложения 2:
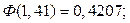  Тогда
Тогда  . .
|
4. Всхожесть семян некоторой культуры 90%. Найти вероятности следующих событий: а) из 100 семян взойдет ровно 80 семян; б) из 100 семян взойдет не менее 70 семян и не более 95 семян.
Решение.
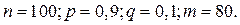
Так как п–велико, то применяем локальную формулу Муавра-Лапласа:
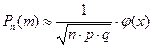 , где
, где 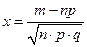 ,
,
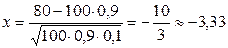 ,
, 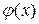 – четная функция,
– четная функция, 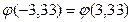 .
.
Находим по таблице приложения 1 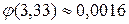 .
.
Тогда  .
.
Так как полученная вероятность очень мала, то событие, что из 100 семян взойдет ровно 80, практически невозможно.
б) 
Так как n большое и m принимает целые значения из промежутка 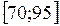 , то применяем интегральную формулу Муавра-Лапласа.
, то применяем интегральную формулу Муавра-Лапласа.
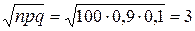 .
.
 .
. 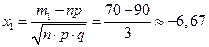 .
.
Находим по таблице приложения 2:
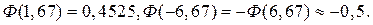
Тогда  .
.
5. Найти вероятность того, что событие А наступит ровно 80 раз при 400 испытаниях, если вероятность появления этого события в каждом испытании равна 0,2.
Решение:
По условию n =400, m=80, p=0,2, q=0,8.
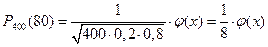
х= 
По таблице приложения 1 находим что φ(0)=0,04986
Тогда Р400(80)= 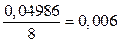 .
.
Дата: 2019-05-28, просмотров: 443.