Формула полной вероятности
Пусть событие А может наступить при условии появления одного из несовместных событий В1, В2,…В n, которые образуют полную группу. Пусть известны вероятности этих событий и условные вероятности события А.
Теорема. Если событие А может произойти только при выполнении одного из событий В1, В2,…В n, которые образуют полную группу несовместных событий, то вероятность события А вычисляется по формуле
 .
.
Эта формула называется формулой полной вероятности.
Пример.
1. В урну, содержащую два шара, опущен белый шар, после чего из нее наудачу извлечен один шар. Найти вероятность того, ч то извлеченный шар окажется белым, если равно возможны все предположения о первоначальном составе шаров.
Решение:
Обозначим события: А – извлечен белый шар;
В1 – первоначально белых шаров в урне не было;
В2 – первоначально в урне был один белый шар;
В3 – первоначально в урне было два белых шара.
Заметим, что 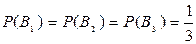 ,
,  ,
, 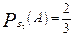 ,
,  . Тогда по формуле полной вероятности
. Тогда по формуле полной вероятности
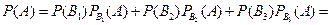
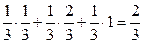 .
.
Формула Байеса
Вновь рассмотрим полную группу несовместных событий В1, В2,…В n вероятности появления которых 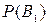 ,
, 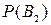 ,…,
,…, 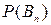 . Событие А может произойти только вместе с каким-либо из событий В1, В2,…В n, которые будем называть гипотезами. Тогда по формуле полной вероятности:
. Событие А может произойти только вместе с каким-либо из событий В1, В2,…В n, которые будем называть гипотезами. Тогда по формуле полной вероятности:
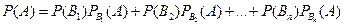 .
.
Если событие А произошло, то это может изменить вероятности гипотез 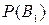 ,
,  ,…,
,…, 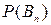 . По теореме умножения вероятностей
. По теореме умножения вероятностей
 ,
,
откуда: 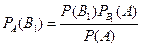 .
.
Аналогично, для остальных гипотез: 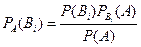 , i=1,2,…,n.
, i=1,2,…,n.
Полученная формула называется формулой Байеса. Здесь Р(А) определяется формулой полной вероятности.
Пример.
1. 30% приборов собирает специалист высокой квалификации и 70% специалист средней квалификации. Надежность работы прибора, собранного специалистом высокой квалификации, 0,9, надежность прибора, собранного специалистом средней квалификации, 0,8. Взятый прибор оказался надежным. Определить вероятность того, что он собран специалистом высокой квалификации.
Решение.
События: А – безотказная работа прибора;
В1 – прибор собран специалистом высокой квалификации;
В2 – прибор собран специалистом средней квалификации.
Выпишем вероятности гипотез:  ,
, 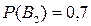 .
.
Условные вероятности события А: 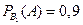 ,
,  .
.
Вероятность события А: 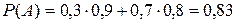 .
.
Определим вероятность гипотезы В1 при условии, что событие А произошло
 .
.
Примеры решения типовых задач
1. В пирамиде 5 винтовок, три из которых снабжены оптическим прицелом. Вероятность того, что стрелок поразит мишень при выстреле из винтовки с прицелом, равна 0,95, для винтовки без прицела соответствующая вероятность равна 0,7. Найти вероятность того, что мишень будет поражена, если стрелок делает один выстрел из произвольной винтовки.
Решение:
Пусть А–мишень поражена;
В1–произведен выстрел из винтовки с прицелом;
В1–выстрел из винтовки без прицела.
Тогда 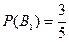 ,
,  и по формуле полной вероятности
и по формуле полной вероятности
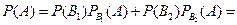
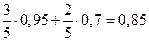 .
.
2. Батарея из трех орудий произвела залп, причем два снаряда попали в цель. Найти вероятность того, что первое орудие попало, если вероятности попадания в цель каждым из орудий равны р1=0,4, р2=0,3, р3=0,5.
Решение.
Обозначим события: А – два орудия попали в цель;
В1 – первое орудие попало в цель; В2 – первое орудие не попало в цель.
Вероятности гипотез: 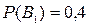 ,
, 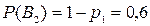 .
.
Условные вероятности события А:
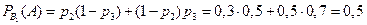 .
.
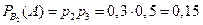 .
.
По формуле Байеса

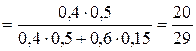 .
.
3. Три компьютерные фирмы представили в контрольное управление компьютеры для выборочной проверки: первая – 20 компьютеров; вторая – 30 компьютеров; третья – 50 компьютеров. Вероятности того, что компьютеры без брака у этих фирм соответственно равны: 0,8; 0,9; 0,7. Был выбран один компьютер, и он оказался без брака. Определить вероятность того, что этот компьютер принадлежит третьей фирме.
Решение.
Здесь события 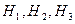 - это выбор компьютера соответственно у первой, второй и третьей фирмы. Вероятности этих событий таковы:
- это выбор компьютера соответственно у первой, второй и третьей фирмы. Вероятности этих событий таковы: 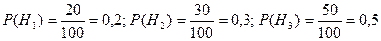 .
.
По формуле полной вероятности определяем вероятность выбора компьютера без брака (событие А): 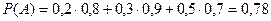 .
.
По формуле Байеса находим искомую вероятность:
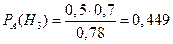 .
.
4. На сборку телевизоров поступают микросхемы от двух поставщиков, причем 70% микросхем от первого поставщика, 30% – от второго. Брак микросхем первого поставщика составляет 2%, второго – 3%. Взятая наудачу микросхема оказалась бракованной. Какова вероятность, что микросхема изготовлена первым поставщиком? Вторым поставщиком?
Решение.
Обозначим
 – взятая наудачу микросхема изготовлена первым поставщиком,
– взятая наудачу микросхема изготовлена первым поставщиком,
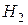 – взятая наудачу микросхема изготовлена вторым поставщиком,
– взятая наудачу микросхема изготовлена вторым поставщиком,
А – взятая наудачу микросхема дефектна – произошло в результате испытания.
Найдем вероятность того, что эта микросхема была изготовлена первым поставщиком по формуле Байеса:
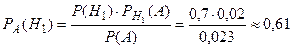 .
.
Аналогично, вероятность того, что микросхема была изготовлена вторым поставщиком:
 .
.
5. По цели произведено три последовательных выстрела. Вероятность попадания при первом выстреле р1=0,3, при втором р2=0,6, при третьем р3=0,8. При одном попадании вероятность поражения цели r1=0,4, при двух попаданиях r2=0,7, при трех попаданиях r3=1. Определить вероятность поражения цели при трех выстрелах.
Решение.
Рассмотрим полную группу несовместных событий:
В1 – было одно попадание;
В2 – было два попадания;
В3 – было три попадания;
В4 – не было ни одного попадания.
Определим вероятность каждого события. По теоремам умножения и сложения вероятностей будем иметь
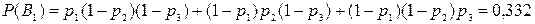 .
.
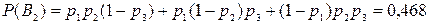 .
.
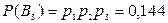 .
.
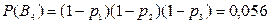 .
.
Пусть событие А – цель поражена. Выпишем условные вероятности поражения цели при осуществлении каждого из событий В1, В2, В3, и В4.
 ,
,  ,
, 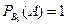 ,
, 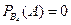 .
.
Тогда по формуле полной вероятности:
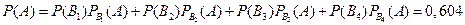
Решение:
Введем обозначения:
события А- поступившая деталь на сборку бракованная;В1 – детали с первого станка;
В2 – детали со второго станка;
В3 – детали с третьего станка;
В4 – детали с четвертого станка.
Воспользуемся формулой полной вероятности где P(B1)= 0,4 ; P(B2)= 0,3 ; P(B3)= 0,2 ; P(B4)= 0,1
где P(B1)= 0,4 ; P(B2)= 0,3 ; P(B3)= 0,2 ; P(B4)= 0,1 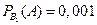 ,
, 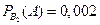 ,
, 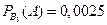 ,
, 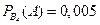 .
.
 7. Для участия в спортивных соревнованиях из 1-ой группы было выделено 4 студента; из 2-ой -6 ; из 3-й – 5 студентов. Вероятность того, что студент каждый из групп попадает в сборную института равны 0,5 ; 0,4; 0,3 соответственно для каждой из групп. Наудачу выбранный участник попал в сборную. К какой из 3-х групп он вероятнее всего принадлежит?Решение: Пусть событие А –произвольно выбранный студент попал в сборную . (Всего было студентов N=4+6+5=15).
7. Для участия в спортивных соревнованиях из 1-ой группы было выделено 4 студента; из 2-ой -6 ; из 3-й – 5 студентов. Вероятность того, что студент каждый из групп попадает в сборную института равны 0,5 ; 0,4; 0,3 соответственно для каждой из групп. Наудачу выбранный участник попал в сборную. К какой из 3-х групп он вероятнее всего принадлежит?Решение: Пусть событие А –произвольно выбранный студент попал в сборную . (Всего было студентов N=4+6+5=15). В1 –студент из первой группы;
В2 – студент из второй группы;
В3 - студент из третьей группы.
Вычислим вероятности того, что студент попавший в сборную принадлежит к той или иной из 3-х групп по формуле Бейеса: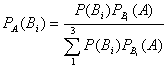 Вероятность принадлежности студента к каждой из групп равна::
Вероятность принадлежности студента к каждой из групп равна:: 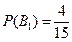 ;
; 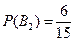 ;
; 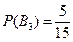 Условные вероятности события А:
Условные вероятности события А:  ,
, 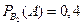
 .
. Вероятность события А:
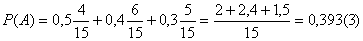
Определим вероятность гипотезы В1 при условии, что событие А произошло
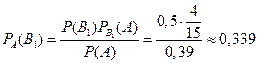 ;
;  ;
;
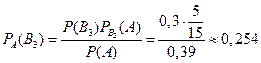
Формула Бернулли
Если производится n независимых испытаний, в каждом из которых вероятность появления события А одна и та же и равна р, то вероятность того, что событие А появится в этих n испытаниях k раз, выражается формулой
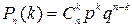 , где q=1-k.
, где q=1-k.
В частности, отсюда Р n(0)=qn, Р n(1)=npqn -1, … , Р n(n)=pn.
С помощью формулы Бернулли обычно вычисляются вероятности тех событий, которые происходят в небольшом числе опытов.
Следствия:
1). Вероятность того, что в n независимых испытаниях событие наступит не менее m1 раз и не более m2 раза, определится по формуле:
Рn(m1  m2)= Рn(m1) +...+ Рn(m2)=
m2)= Рn(m1) +...+ Рn(m2)= 
2). Вероятность того, что в n независимых испытаниях событие наступит хотя бы один раз, определится по формуле:
Рn( 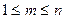 )=
)=  =1
=1
Примеры.
1. В урне 20 белых и 10 черных шаров. Вынули 4 шара, причем каждый вынутый шар возвращают в урну перед извлечением следующего и шары в урне перемешивают. Найти вероятность того, что из четырех вынутых шаров окажется 2 белых.
Решение:
Событие А – достали белый шар. Тогда вероятности 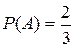 ,
, 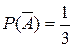 . По формуле Бернулли требуемая вероятность
. По формуле Бернулли требуемая вероятность
 .
.
2. Определить вероятность того, что в семье, имеющей 5 деталей, будет не больше трех девочек. Вероятности рождения мальчика и девочки предполагаются одинаковыми.
Решение:
Вероятность рождения девочки 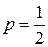 , тогда
, тогда 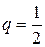 .
.
Найдем вероятности того, что в семье нет девочек, родилась одна, две или три девочки:
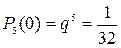 ,
,  ,
,
 ,
, 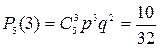 .
.
Следовательно, искомая вероятность
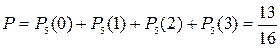 .
.
3. По цели производится 5 выстрелов. Вероятность попадания для каждого выстрела равна 0,4. Найти вероятность того, что в цель попали не менее трех раз.
Решение:
Вероятность не менее трех попаданий складывается из вероятности пяти попаданий, четырех попаданий и трех попаданий.
Т.к. выстрелы независимы, то можно применить формулу Бернулли вероятности того, что в п испытаниях событие с вероятностью р наступает ровно т раз.
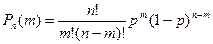
В случае пяти попаданий из пяти возможных: 
Четыре попадания из пяти выстрелов: 
Три попадания из пяти: 
Окончательно, получаем вероятность не менее трех попаданий из пяти выстрелов:
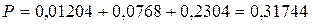
4. Всхожесть семян некоторой культуры 90%. Найти вероятность того, что из 10 случайно отобранных семян взойдет не менее 8.
Решение:
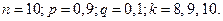
Так как проводится п независимых испытаний и п невелико, то применяем формулу Бернулли:
 .
.
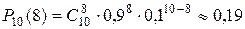
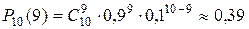 .
.
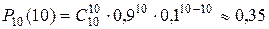 .
.
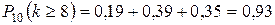 .
.
Дата: 2019-05-28, просмотров: 409.