.

Примеры решения типовых задач

1. В урне 10 белых, 15 черных, 20 синих и 25 красных шаров. Вынули один шар. Найти вероятность того, что вынутый шар: а) синий или черный; б) белый, черный или синий.

Решение.

Обозначим следующие события:

Б – вынули белый шар, 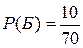; Ч – вынули черный шар, ;

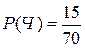С – вынули синий шар, 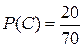; К – вынули красный шар, .

Тогда искомые вероятности будут:

а) .

б)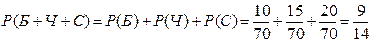

или .

2. На стеллаже в библиотеке стоит 15 учебников, причем 5 из них в переплете. Библиотекарь берет три учебника. Найти вероятность того, что хотя бы один из взятых учебников окажется в переплете.

Решение.

Рассмотрим два способа решения задачи.

Первый способ. Пусть события:

А – хотя бы один учебник в переплете;

В – один из взятых учебников в переплете, два – без переплета;

С – два в переплете, один без переплета;

D – все три учебника в переплете.

Очевидно, А=В+С+D. Найдем вероятности событий В, С, и D.

, , .

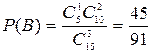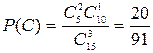Тогда

.

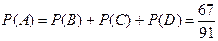Второй способ. Вновь А – хотя бы один учебник в переплете;

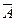 - ни один из взятых учебников не имеет переплета.

Так как события А и 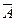 противоположные, то

.

3. Экспедиция издательства отправила газеты в три почтовых отделения. Вероятность своевременной доставки газет в первое отделение равна 0,95, во второе - 0,9, в третье - 0,8. Найти вероятность следующих событий: а) только одно отделение получит газеты вовремя; б) хотя бы одно отделение получит газеты с опозданием.

Решение:

а). Введем обозначения:

события А1 - (газеты доставлены своевременно в первое отделение),

А2 - (газеты доставлены своевременно во второе отделение),

А3 - (газеты доставлены своевременно в третье отделение),

 Х - (только одно отделение получит газеты вовремя).

По условию:

P(A1)=0,95; P(A2) = 0,9; P(A3)=0,8.

Событие Х произойдет, если или газеты доставлены своевременно в 1 отделение, и доставлены не вовремя во 2 и 3, или газеты доставлены своевременно в 2 отделение, и доставлены не вовремя во 1 и 3, или газеты доставлены своевременно в 3 отделение, и доставлены не вовремя во 2 и 1.

Таким образом:

Так как события А1, А2, А3 - независимые, по теоремам сложения и умножения получаем

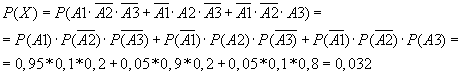
б). Найдем вероятность события Y - (хотя бы одно отделение получит газеты с опозданием).

Введем противоположное событие 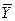- (все отделения получат газеты вовремя).

Вероятность этого события:

Тогда вероятность события Y:

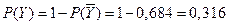
4. Для сигнализации об аварии установлены два независимо работающих сигнализатора. Вероятность того, что при аварии сигнализатор сработает, равна 0,95 для первого сигнализатора и 0,9 для второго. Найти вероятность того, что при аварии сработает только один сигнализатор.

Решение:

Введем обозначения:

события А1 - (при аварии сработает первый сигнализатор);

А2 - (при аварии сработает второй сигнализатор);

 Х - (при аварии сработает только один сигнализатор).

по условию задачи P(A1)=0,95, P(A2)=0,9.

Событие Х произойдет, если при аварии сработает первый сигнализатор и не сработает второй, или если при аварии сработает второй сигнализатор и не сработает первый, то есть:

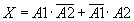
Тогда вероятность события Х по теоремам сложения и умножения вероятностей равна

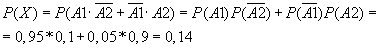
5. Вероятность попадания в цель у первого стрелка 0,8, у второго – 0,9. Стрелки делают по выстрелу. Найти вероятность: а) двойного попадания; б) хотя бы одного попадания; г) одного попадания.

Решение.

Пусть А – попадание первого стрелка, Р(А)=0,8;

В – попадание второго стрелка, Р(В)=0,9.

Тогда 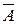 - промах первого, ;

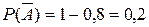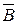 - промах второго, .

Найдем нужные вероятности.

а) АВ – двойное попадание, Р(АВ)=Р(А)Р(В)=0,72.

б) 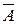 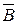- двойной промах, .

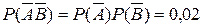в) А+В – хотя бы одно попадание, 

.

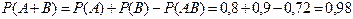г) 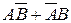 - одно попадание,

.

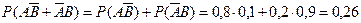6. Студент разыскивает нужную ему формулу в трех справочниках. Вероятности того, что формула содержится в первом, втором и третьем справочниках равны 0,6; 0,7 и 0,8. Найти вероятности того, что формула содержится 1) только в одном справочнике; 2) только в двух справочниках; 3) во всех трех справочниках.

Решение.

А – формула содержится в первом справочнике;

В – формула содержится во втором справочнике;

С – формула содержится в третьем справочнике.

Воспользуемся теоремами сложения и умножения вероятностей.

1. 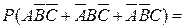0,6·0,3·0,2+0,4·0,7·0,2+0,4·0,3·0,8=0,188.

2. .

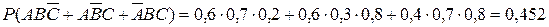3. Р(АВС)=0,6·0,7·0,8=0,336.

7. Из 10 деталей 7 – стандартные. Наудачу берут 6 деталей. Найти вероятность того, что среди них: а) не более одной нестандартной; б) не более двух нестандартных.

Решение.

а). Обозначим события А – среди взятых 6 деталей нестандартных нет;

В – в 6 выбранных деталях одна нестандартная. Тогда А+В – среди 6 деталей не более одной нестандартной. Найдем Р(А+В). Заметим, что

,

.

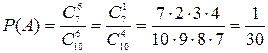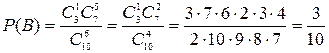Откуда

.

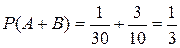б). Пусть теперь событие А – в шести взятых деталях не более двух нестандартных. Тогда 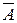 - в выбранных деталях более двух нестандартных, т.е. три.

.

.