Классическое определение вероятности связано с понятием благоприятствующего исхода.

Определение. Исход называется благоприятствующим, данному событию, если его появление влечет за собой наступление этого события.

Определение . Вероятность события А равна отношению числа благоприятствующих исходов к общему числу всех возможных исходов:

,

где m – число благоприятствующих событию А исходов;

n - общее число возможных исходов.

Свойства вероятности события

1. Вероятность достоверного события равна единице,

2. Вероятность невозможного события равна нулю.

Таким образом, значение вероятности любого события – есть положительное число, заключенное между нулем и единицей.

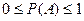
Статистическое определение вероятности

Данное понятие основано на том, насколько часто будет появляться данное событие в произведенных испытаниях.

Статистическое определение вероятности связано с понятием относительной частоты появления события А в опытах.

Определение. Относительной частотой события А называется отношение числа опытов, в результате которых произошло событие А к общему числу опытов:

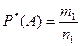, где m ₁ – число появлений события А в серии из n ₁ испытаний.

Вероятностью р события А называется отношение числа m благоприятствующих случаев к числу всех возможных случаев n, образующих полную группу равновозможных несовместных событий

.

Заметим, что вероятность достоверного события р=1. Вероятность невозможного события р=0. Кроме того из определения вероятности следует, что для любого события А

.

Примеры решения типовых задач

1. В урне находятся 6 белых и 5 черных шаров. Из урны одновременно вынимают два шара. Какова вероятность того, что оба шара белые (событие А)?

Решение.

Здесь число равновозможных независимых исходов составляет .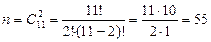

Событию А благоприятствуют  исходов. Следовательно,

2. В урне 10 пронумерованных шаров с номерами от 1 до 10. Вынули один шар. Какова вероятность того, что номер вынутого шара не превосходит 10?

Решение.

Пусть событие А – номер вынутого шара не превосходит 10. Число случаев благоприятствующих появлению события А равно числу всех возможных случаев m=n=10. Следовательно, Р(А)=1.

3. В урне 15 шаров: 5 белых и 10 черных. Какова вероятность вынуть из урны синий шар?

Решение.

Так как синих шаров в урне нет, то m=0, n=15. Следовательно, искомая вероятность р=0.

4. Из колоды в 36 карт вынимается одна карта. Какова вероятность появления карты пиковой масти?

Решение.

Здесь всего случаев n=36.

Обозначим: Событие А – появление карты пиковой масти.

Число случаев, благоприятствующих появлению события А, m=9. Следовательно, .

5. В урне 10 шаров: 6 белых и 4 черных. Вынули два шара. Какова вероятность, что оба шара белые?

Решение:

Обозначим: событие А- вынуть два белых шара.

Вынуть два шара из десяти можно следующим числом способов: .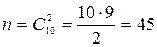

Число случаев, когда среди этих двух шаров будут оба белые, равно .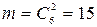

Искомая вероятность будет .

6. В цехе работают 6 мужчин и 4 женщины. По табельным номерам наудачу отобраны 7 человек. Найти вероятность того, что среди отобранных лиц три женщины.

Решение:

Обозначим: событие А- среди отобранных лиц три женщины.

Общее число возможных исходов равно числу способов, которыми можно отобрать 7 человек из 10, т.е. .

Найдем число исходов, благоприятствующих интересующему нас событию: трех женщин можно выбрать из четырех 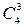 способами; при этом остальные четыре человека должны быть мужчинами, их можно отобрать  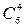способами. Следовательно, число благоприятствующих исходов равно .

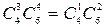Искомая вероятность .