РАЗДЕЛ I. СЛУЧАЙНЫЕ СОБЫТИЯ
ГЛАВА 1. СОБЫТИЕ И ВЕРОЯТНОСТЬ
1.1. Некоторые формулы комбинаторики
Рассмотрим некоторое множество Х, состоящее из n элементов 
. Будем выбирать из этого множества различные упорядоченные подмножества Z из k элементов.
Определение. Размещением из n элементов множества Х по k элементам называется комбинации составленные из данных n элементов по k которые отличаются либо элементом, либо порядком следования.
Число размещений из n элементов по k равно:
.
Пример.
Расписание одного дня содержит 5 уроков. Определить количество таких расписаний при выборе из 11 дисциплин.
Решение:
Количество различных расписаний можно определить с помощью формулы комбинаторики для размещения по 5 из 11 элементов. Выбор размещения определяется тем, что при построении расписания необходимо учитывать порядок следования уроков.
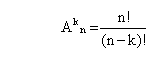
При данных условиях можно составить 55440 различных расписаний.
Частный случай размещения при n=k называется перестановкой из n элементов.
Определение. Перестановкой из n различный элементов называют расположение этих элементов в определенном порядке и отличающихся друг от друга только порядком следования.
Число различных перестановок из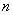 
элементов обозначается Pn и равно 
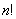, т.е.
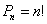
Примеры.
1. Из цифр 1, 2, 3, 4, 5 составлены всевозможные пятизначные числа без повторения цифр. Сколько среди этих чисел таких, которые начинаются цифрой 3?
Решение:
Поставим цифру 3 на первое место и зафиксируем ее. А остальные четыре цифры будем переставлять для получения различных чисел. Таким образом, количество чисел будет определяться количеством перестановок среди чисел 1, 2, 4, 5.
Чтобы его найти, воспользуемся формулой комбинаторики:
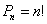
Рn = 4! = 24. т.е. из цифр 1, 2, 3, 4, 5 можно составить 24 пятизначных числа без повторения цифр, которые начинаются цифрой 3.
2. Порядок выступления 7 участников конкурса определяется жребием. Сколько различных вариантов жеребьевки при этом возможно?
Решение:
Каждый вариант жеребьевки отличается только порядком участников конкурса, т.е. является перестановкой из 7 элементов. Их число равно
Пусть теперь из множества Х выбирается неупорядоченное подмножество Z , т.е. два подмножества Z1 и Z2 из k элементов, состоящие из одних и тех же элементов и отличающиеся их порядком будем считать одинаковыми.
Определение . Сочетаниями из n элементов по k называются подмножества из k элементов, отличающиеся друг от друга хотя бы одним элементом.
Общее число всех сочетаний из n по k обозначается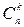 
и равно
.
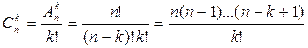В дальнейшем будем считать 
.
Примеры.
1. В группе из 27 человек нужно выбрать трех делегатов на профсоюзную конференцию. Найдем сколькими способами это можно сделать.
Решение:
.
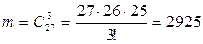2. Сколькими способами можно составить бригаду из трех человек для дежурства в группе из 30 человек.
Решение:
Поскольку порядок расположения людей в бригаде не фиксируется и люди не повторяются, то мы имеем случай сочетаний из 30 элементов по 3 без повторений:
.
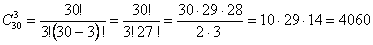Таким образом, бригаду дежурных из трех человек в группе из 30 человек можно выбрать 4060 различными способами.
3. В шахматном турнире участвуют 16 человек. Сколько партий должно быть сыграно в турнире, если между любыми двумя участниками должна быть сыграна одна партия?
Решение:
Каждая партия играется двумя участниками из 16 и отличается от других только составом пар участников, т.е. представляет собой сочетания из 16 элементов по 2.
Их число равно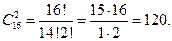 
Основные понятия теории вероятности
К основным понятиям теории вероятности относятся испытания и события.
Под испытанием (опытом) понимают выполнение определенных условий или действий, в результате которых непременно произойдет какое-либо событие.
Определение. Достоверным событием называется событие, которое непременно произойдет в результате опыта. Событие называется невозможным, если оно никогда не произойдет в результате опыта.
Определение. События называются несовместными, если наступление одного из них исключает наступление любого другого. В противном случае события называются совместными.
Определение. Несколько событий в данном опыте образуют полную группу событий, если в результате опыта непременно должно произойти хотя бы одно из них.
Определение. События называются равновозможными, если нет оснований считать, что одно из них появится в результате опыта с большей вероятностью.
Каждый из равновозможных исходов испытаний (опытов), образующих полную группу называется элементарным исходом. Их обычно обозначают буквами w 1 , w 2 , …, w n.
Каждое событие обладает какой-то степенью возможности. Численная мера возможности появления рассматриваемого события – это вероятность события. Вероятность события А обозначается Р(А). Наиболее широкое распространение получили два определения вероятности события: классическое и статистическое.
Дата: 2019-05-28, просмотров: 275.
