МАТЕМАТИКА
Методические рекомендации по организации и выполнению расчетно-графической работы № 3 для студентов ИДО, направления подготовки 20.03.01 Техносферная безопасность
Тюмень, 2016
УДК
ББК
Составитель: доцент кафедры математики и информатики, к.п.н., М.В. Виноградова
Математика. Методические указания и варианты расчетно-графической работы № 3 для студентов института дистанционного образования направления подготовки 20.03.01 Техносферная безопасность / М.В. Виноградова – Тюмень, 2016 – 93 с. –электронный ресурс
Методические указания разработаны для студентов института дистанционного образования направления подготовки 20.03.01 Техносферная безопасность. Предназначены для выполнения расчетно-графической работы № 3 по дисциплине «Математика».
Рецензент: Н.Н. Мальчукова– к.п.н., доцент кафедры математики и информатики ГАУ Северного Зауралья
УТВЕРЖДЕНО
на заседании кафедры математики и информатики
протокол № 3 от 30 ноября 2016 г.
методической комиссией механико-технологического института
протокол 3 № от 6 декабря 2016 г.
© ГАУ Северного Зауралья, 2016
© М.В. Виноградова, 2016
Оглавление
Введение
Требования к выполнению и оформлению контрольных работ.
РАЗДЕЛ I.
СЛУЧАЙНЫЕ СОБЫТИЯ
Глава 1.
События и вероятность
1.1.
Некоторые формулы комбинаторики
1.2.
Основные понятия теории вероятности
1.3.
Классическое определение вероятности
1.4.
Статистическое определение вероятности
Примеры решения типовых задач 9
Глава 2.
Теоремы сложения вероятностей
2.1.
Сложение вероятностей
2.2.
Умножение вероятностей независимых событий
2.3.
Условная вероятность
Примеры решения типовых задач 12
Глава 3.
Следствие теорем сложения и умножения
3.1.
. Формула полной вероятности
3.2.
Формула Байеса
Примеры решения типовых задач 16
Глава 4.
Повторение испытаний
4.1
Формула Бернулли
4.2.
Локальная и интегральная формулы Муавра- Лапласа
4.3.
Формула Пуассона
Примеры решения типовых задач
Контрольный тест после изучения раздела I «Случайные события»
РАЗДЕЛ II.
СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
Глава 5.
Дискретная случайная величина
5.1.
Основные понятия случайных величин
5.2.
Числовые характеристики дискретной случайной величины
Примеры решения типовых задач 28
Глава 6.
Непрерывная случайная величина
6.1.
Функция и плотность распределения непрерывной случайной величины
6.2.
Числовые характеристики непрерывной случайной величины
Примеры решения типовых задач
Контрольный тест после изучения раздела II «Случайные величины»
РАЗДЕЛ III.
ВЫБОРОЧНЫЙ МЕТОД
Глава 7.
Выборочный метод
Генеральная и выборочная совокупности. Виды выборки
Статистическое распределение выборки
Графическое изображение статистического распределения выборки и эмпирической функции распределения.
Глава 8.
Статистические оценки параметров распределения
Оценки параметров распределения
Понятия генеральной и выборочной средней. Формулы вычисления
Понятия генеральной и выборочной дисперсий и формулы вычисления
Точность оценки, доверительная вероятность (надежность). Доверительный интервал.
РАЗДЕЛ IV.
СТАТИСТИЧЕСКАЯ ПРОВЕРКА СТАТИСТИЧЕСКИХ ГИПОТЕЗ
Глава 9.
Проверка гипотез
9.1.
Понятие статистической гипотезы
9.2.
Критическая область. Область принятия гипотезы. Критические точки
9.3
Проверка гипотезы о нормальном распределении генеральной совокупности. Критерий согласия Пирсона
9.4
Методика вычисления теоретических частот нормального распределения
Пример решения типовой задачи
Контрольный тест после изучения раздела «Статистическая проверка статистических гипотез»
РАЗДЕЛ V
ЭЛЕМЕНТЫ ТЕОРИИ КОРРЕЛЯЦИИ
Глава 10.
Элементы корреляционного анализа
10.1.
Основные понятия корреляционного анализа.
10.2.
Корреляционная таблица и корреляционное поле
10.3
Выборочное уравнение регрессии
10.4.
Выборочный коэффициент корреляции
10.5.
Оценка тесноты любой связи
Пример решения типовой задачи
Контрольный тест после изучения раздела V «Элементы теории корреляции»
Задания для контрольной работы № 3
Контрольные вопросы к итоговой аттестации по предмету
Учебно-методическое и информационное обеспечение дисциплины
Выполнение и оформление контрольных работ
1. Слушатели выполняют контрольную работу в соответствии с учебным планом в сроки, установленные ИДО.
2. Каждая контрольная работа выполняется в отдельной тетради в клеточку, ручкой любого цвета, кроме зеленого и красного, аккуратно и разборчивым почерком, чертежи выполняются простым карандашом с использованием инструмента.
3. На титульном листе следует указать фамилию, имя, отчество слушателя, его адрес с указанием почтового индекса, номер зачетной книжки, номер варианта.
4. Задания в контрольных работах выполняются по порядку, согласно расположению их в варианте.
5. На заключительном листе контрольных работ следует указать список литературы, которым Вы пользовались при их выполнении.
6. Если контрольные работы выполнены с нарушением всех вышеперечисленных указаний или не полностью, то они возвращаются слушателю для доработки без проверки.
7. Если работы не зачтены, внимательно изучите все замечания рецензента. Переделайте работы в соответствии с рекомендациями рецензента.
8. Переделанные работы предоставляются на проверку вместе с незачтенными работами.
9. Слушатель выполняет тот вариант контрольных работ, который совпадает с последней цифрой его учебного шифра.
При этом если предпоследняя цифра учебного шифра – нечетное число (1,3,5,7,9),то номера задач для соответствующего варианта даны в таблице № 1; если же предпоследняя цифра учебного шифра – четное число или ноль (2,4,6,8,0), то номера задач для соответствующего варианта даны в таблице № 2.
Таблица № 1.
| № варианта | ||||||||
Таблица № 2.
| № варианта | ||||||||
РАЗДЕЛ I. СЛУЧАЙНЫЕ СОБЫТИЯ
ГЛАВА 1. СОБЫТИЕ И ВЕРОЯТНОСТЬ
1.1. Некоторые формулы комбинаторики
Рассмотрим некоторое множество Х, состоящее из n элементов  . Будем выбирать из этого множества различные упорядоченные подмножества Z из k элементов.
. Будем выбирать из этого множества различные упорядоченные подмножества Z из k элементов.
Определение. Размещением из n элементов множества Х по k элементам называется комбинации составленные из данных n элементов по k которые отличаются либо элементом, либо порядком следования.
Число размещений из n элементов по k равно:
 .
.
Пример.
Расписание одного дня содержит 5 уроков. Определить количество таких расписаний при выборе из 11 дисциплин.
Решение:
Количество различных расписаний можно определить с помощью формулы комбинаторики для размещения по 5 из 11 элементов. Выбор размещения определяется тем, что при построении расписания необходимо учитывать порядок следования уроков.
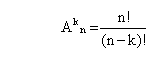

При данных условиях можно составить 55440 различных расписаний.
Частный случай размещения при n=k называется перестановкой из n элементов.
Определение. Перестановкой из n различный элементов называют расположение этих элементов в определенном порядке и отличающихся друг от друга только порядком следования.
Число различных перестановок из 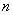 элементов обозначается Pn и равно
элементов обозначается Pn и равно 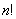 , т.е.
, т.е.
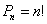
Примеры.
1. Из цифр 1, 2, 3, 4, 5 составлены всевозможные пятизначные числа без повторения цифр. Сколько среди этих чисел таких, которые начинаются цифрой 3?
Решение:
Поставим цифру 3 на первое место и зафиксируем ее. А остальные четыре цифры будем переставлять для получения различных чисел. Таким образом, количество чисел будет определяться количеством перестановок среди чисел 1, 2, 4, 5.
Чтобы его найти, воспользуемся формулой комбинаторики:
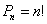
Рn = 4! = 24. т.е. из цифр 1, 2, 3, 4, 5 можно составить 24 пятизначных числа без повторения цифр, которые начинаются цифрой 3.
2. Порядок выступления 7 участников конкурса определяется жребием. Сколько различных вариантов жеребьевки при этом возможно?
Решение:
Каждый вариант жеребьевки отличается только порядком участников конкурса, т.е. является перестановкой из 7 элементов. Их число равно

Пусть теперь из множества Х выбирается неупорядоченное подмножество Z , т.е. два подмножества Z1 и Z2 из k элементов, состоящие из одних и тех же элементов и отличающиеся их порядком будем считать одинаковыми.
Определение . Сочетаниями из n элементов по k называются подмножества из k элементов, отличающиеся друг от друга хотя бы одним элементом.
Общее число всех сочетаний из n по k обозначается 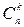 и равно
и равно
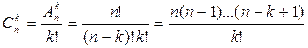 .
.
В дальнейшем будем считать  .
.
Примеры.
1. В группе из 27 человек нужно выбрать трех делегатов на профсоюзную конференцию. Найдем сколькими способами это можно сделать.
Решение:
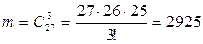 .
.
2. Сколькими способами можно составить бригаду из трех человек для дежурства в группе из 30 человек.
Решение:
Поскольку порядок расположения людей в бригаде не фиксируется и люди не повторяются, то мы имеем случай сочетаний из 30 элементов по 3 без повторений:
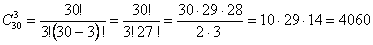 .
.
Таким образом, бригаду дежурных из трех человек в группе из 30 человек можно выбрать 4060 различными способами.
3. В шахматном турнире участвуют 16 человек. Сколько партий должно быть сыграно в турнире, если между любыми двумя участниками должна быть сыграна одна партия?
Решение:
Каждая партия играется двумя участниками из 16 и отличается от других только составом пар участников, т.е. представляет собой сочетания из 16 элементов по 2.
Их число равно 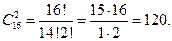
Основные понятия теории вероятности
К основным понятиям теории вероятности относятся испытания и события.
Под испытанием (опытом) понимают выполнение определенных условий или действий, в результате которых непременно произойдет какое-либо событие.
Определение. Достоверным событием называется событие, которое непременно произойдет в результате опыта. Событие называется невозможным, если оно никогда не произойдет в результате опыта.
Определение. События называются несовместными, если наступление одного из них исключает наступление любого другого. В противном случае события называются совместными.
Определение. Несколько событий в данном опыте образуют полную группу событий, если в результате опыта непременно должно произойти хотя бы одно из них.
Определение. События называются равновозможными, если нет оснований считать, что одно из них появится в результате опыта с большей вероятностью.
Каждый из равновозможных исходов испытаний (опытов), образующих полную группу называется элементарным исходом. Их обычно обозначают буквами w 1 , w 2 , …, w n.
Каждое событие обладает какой-то степенью возможности. Численная мера возможности появления рассматриваемого события – это вероятность события. Вероятность события А обозначается Р(А). Наиболее широкое распространение получили два определения вероятности события: классическое и статистическое.
Примеры решения типовых задач
1. В урне находятся 6 белых и 5 черных шаров. Из урны одновременно вынимают два шара. Какова вероятность того, что оба шара белые (событие А)?
Решение.
Здесь число равновозможных независимых исходов составляет 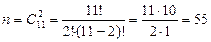 .
.
Событию А благоприятствуют  исходов. Следовательно,
исходов. Следовательно, 
2. В урне 10 пронумерованных шаров с номерами от 1 до 10. Вынули один шар. Какова вероятность того, что номер вынутого шара не превосходит 10?
Решение.
Пусть событие А – номер вынутого шара не превосходит 10. Число случаев благоприятствующих появлению события А равно числу всех возможных случаев m=n=10. Следовательно, Р(А)=1.
3. В урне 15 шаров: 5 белых и 10 черных. Какова вероятность вынуть из урны синий шар?
Решение.
Так как синих шаров в урне нет, то m=0, n=15. Следовательно, искомая вероятность р=0.
4. Из колоды в 36 карт вынимается одна карта. Какова вероятность появления карты пиковой масти?
Решение.
Здесь всего случаев n=36.
Обозначим: Событие А – появление карты пиковой масти.
Число случаев, благоприятствующих появлению события А, m=9. Следовательно,  .
.
5. В урне 10 шаров: 6 белых и 4 черных. Вынули два шара. Какова вероятность, что оба шара белые?
Решение:
Обозначим: событие А- вынуть два белых шара.
Вынуть два шара из десяти можно следующим числом способов: 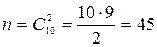 .
.
Число случаев, когда среди этих двух шаров будут оба белые, равно 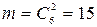 .
.
Искомая вероятность будет  .
.
6. В цехе работают 6 мужчин и 4 женщины. По табельным номерам наудачу отобраны 7 человек. Найти вероятность того, что среди отобранных лиц три женщины.
Решение:
Обозначим: событие А- среди отобранных лиц три женщины.
Общее число возможных исходов равно числу способов, которыми можно отобрать 7 человек из 10, т.е.  .
.
Найдем число исходов, благоприятствующих интересующему нас событию: трех женщин можно выбрать из четырех 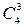 способами; при этом остальные четыре человека должны быть мужчинами, их можно отобрать
способами; при этом остальные четыре человека должны быть мужчинами, их можно отобрать 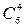 способами. Следовательно, число благоприятствующих исходов равно
способами. Следовательно, число благоприятствующих исходов равно 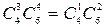 .
.
Искомая вероятность  .
.
Сложение вероятностей
Определение. Суммой двух событий А и B называется событие С, состоящее в появлении хотя бы одного из этих событий.
Сумма обозначается: С=А+В=А или В.
Теорема о сложении вероятностей. Вероятность появления одного из двух несовместных событий равна сумме вероятностей этих событий.
Р(А или В)=Р(А)+Р(В).
Определение. Два события называются противоположными, если они несовместны и образуют полную группу. Если событие обозначим через А, то противоположное ему – через 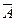 .
.
Так как при испытании обязательно произойдет или событие А или событие 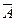 , то согласно теореме о сложении вероятностей получаем
, то согласно теореме о сложении вероятностей получаем 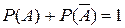 .
.
Если случайные события А1, А2,…, А n образуют полную группу несовместных событий, то имеет место равенство
 .
.
Определение. Случайные события А и B называются совместными, если при данном испытании могут произойти оба эти события. Событие, заключающееся в совмещении событий А и B, будем обозначать А и В или АВ.
Теорема. Вероятность суммы совместных событий вычисляется по формуле
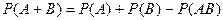 .
.
Пример.
1. В ящике 10 красных и 5 синих пуговиц. Вынимаются наудачу две пуговицы. Какова вероятность, что пуговицы будут одноцветными?
Решение.
Событие A={вынуты пуговицы одного цвета} можно представить в виде суммы  , где события
, где события  и
и  означают выбор пуговиц красного и синего цвета соответственно.
означают выбор пуговиц красного и синего цвета соответственно.
Вероятность вытащить две красные пуговицы равна 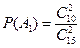 , а вероятность вытащить две синие пуговицы
, а вероятность вытащить две синие пуговицы  . Так как события
. Так как события  и
и  не могут произойти одновременно, то в силу теоремы сложения
не могут произойти одновременно, то в силу теоремы сложения
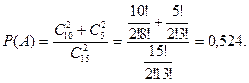
Условная вероятность
Определение. Событие А называется зависимым от события В, если вероятность появления события А зависит от того, произошло или нет событие В.
Вероятность того, что произошло А при условии, что произошло событие В, будем обозначать P В(A) и называть условной вероятностью события А при условии В.
Справедливы следующие теоремы.
Теорема. Вероятность совместного появления двух зависимых событий равна произведению вероятности одного из них на условную вероятность второго, вычисленную при условии, что первое событие произошло, т.е.
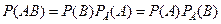 .
.
В частности, отсюда получаем 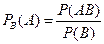 .
.
Примеры.
1. Вероятность изготовления годного изделия данным станком 0,9. Вероятность появления изделия первого сорта среди годных изделий 0,8. Определить вероятность изготовления изделия первого сорта данным станком.
Решение:
Событие В – изготовление годного изделия данным станком; событие А – появление изделия первого сорта. Очевидно, Р(В)=0,9,  . Искомая вероятность будет
. Искомая вероятность будет
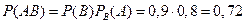 .
.
2. К экзамену надо подготовить 25 вопросов. Студент пришел на экзамен, зная 20. Какова вероятность того, что студент ответит на все три вопроса билета?
Решение.
Пусть события: А – студент знает первый вопрос;
В – студент знает второй вопрос;
С – студент знает третий вопрос.
Примеры решения типовых задач
1. В урне 10 белых, 15 черных, 20 синих и 25 красных шаров. Вынули один шар. Найти вероятность того, что вынутый шар: а) синий или черный; б) белый, черный или синий.
Решение.
Обозначим следующие события:
Б – вынули белый шар, 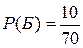 ; Ч – вынули черный шар,
; Ч – вынули черный шар, 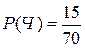 ;
;
С – вынули синий шар, 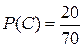 ; К – вынули красный шар,
; К – вынули красный шар,  .
.
Тогда искомые вероятности будут:
а)  .
.
б) 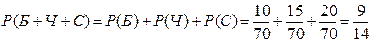
или  .
.
2. На стеллаже в библиотеке стоит 15 учебников, причем 5 из них в переплете. Библиотекарь берет три учебника. Найти вероятность того, что хотя бы один из взятых учебников окажется в переплете.
Решение.
Рассмотрим два способа решения задачи.
Первый способ. Пусть события:
А – хотя бы один учебник в переплете;
В – один из взятых учебников в переплете, два – без переплета;
С – два в переплете, один без переплета;
D – все три учебника в переплете.
Очевидно, А=В+С+D. Найдем вероятности событий В, С, и D.
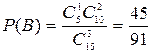 ,
, 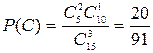 ,
,  .
.
Тогда
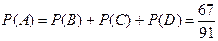 .
.
Второй способ. Вновь А – хотя бы один учебник в переплете;
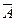 - ни один из взятых учебников не имеет переплета.
- ни один из взятых учебников не имеет переплета.
Так как события А и 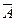 противоположные, то
противоположные, то
 .
.
3. Экспедиция издательства отправила газеты в три почтовых отделения. Вероятность своевременной доставки газет в первое отделение равна 0,95, во второе - 0,9, в третье - 0,8. Найти вероятность следующих событий: а) только одно отделение получит газеты вовремя; б) хотя бы одно отделение получит газеты с опозданием.
Решение:
а). Введем обозначения:
события А1 - (газеты доставлены своевременно в первое отделение),
А2 - (газеты доставлены своевременно во второе отделение),
А3 - (газеты доставлены своевременно в третье отделение),
Х - (только одно отделение получит газеты вовремя).
По условию:
P(A1)=0,95; P(A2) = 0,9; P(A3)=0,8.
Событие Х произойдет, если или газеты доставлены своевременно в 1 отделение, и доставлены не вовремя во 2 и 3, или газеты доставлены своевременно в 2 отделение, и доставлены не вовремя во 1 и 3, или газеты доставлены своевременно в 3 отделение, и доставлены не вовремя во 2 и 1.
Таким образом:

Так как события А1, А2, А3 - независимые, по теоремам сложения и умножения получаем
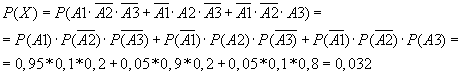
б). Найдем вероятность события Y - (хотя бы одно отделение получит газеты с опозданием).
Введем противоположное событие 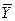 - (все отделения получат газеты вовремя).
- (все отделения получат газеты вовремя).
Вероятность этого события:

Тогда вероятность события Y:
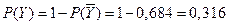
4. Для сигнализации об аварии установлены два независимо работающих сигнализатора. Вероятность того, что при аварии сигнализатор сработает, равна 0,95 для первого сигнализатора и 0,9 для второго. Найти вероятность того, что при аварии сработает только один сигнализатор.
Решение:
Введем обозначения:
события А1 - (при аварии сработает первый сигнализатор);
А2 - (при аварии сработает второй сигнализатор);
Х - (при аварии сработает только один сигнализатор).
по условию задачи P(A1)=0,95, P(A2)=0,9.
Событие Х произойдет, если при аварии сработает первый сигнализатор и не сработает второй, или если при аварии сработает второй сигнализатор и не сработает первый, то есть:
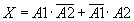
Тогда вероятность события Х по теоремам сложения и умножения вероятностей равна
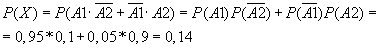
5. Вероятность попадания в цель у первого стрелка 0,8, у второго – 0,9. Стрелки делают по выстрелу. Найти вероятность: а) двойного попадания; б) хотя бы одного попадания; г) одного попадания.
Решение.
Пусть А – попадание первого стрелка, Р(А)=0,8;
В – попадание второго стрелка, Р(В)=0,9.
Тогда 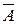 - промах первого,
- промах первого, 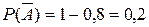 ;
;
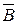 - промах второго,
- промах второго,  .
.
Найдем нужные вероятности.
а) АВ – двойное попадание, Р(АВ)=Р(А)Р(В)=0,72.
б) 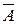
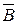 - двойной промах,
- двойной промах, 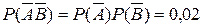 .
.
в) А+В – хотя бы одно попадание,
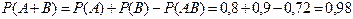 .
.
г) 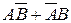 - одно попадание,
- одно попадание,
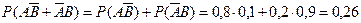 .
.
6. Студент разыскивает нужную ему формулу в трех справочниках. Вероятности того, что формула содержится в первом, втором и третьем справочниках равны 0,6; 0,7 и 0,8. Найти вероятности того, что формула содержится 1) только в одном справочнике; 2) только в двух справочниках; 3) во всех трех справочниках.
Решение.
А – формула содержится в первом справочнике;
В – формула содержится во втором справочнике;
С – формула содержится в третьем справочнике.
Воспользуемся теоремами сложения и умножения вероятностей.
1. 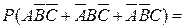 0,6·0,3·0,2+0,4·0,7·0,2+0,4·0,3·0,8=0,188.
0,6·0,3·0,2+0,4·0,7·0,2+0,4·0,3·0,8=0,188.
2. 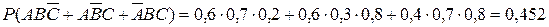 .
.
3. Р(АВС)=0,6·0,7·0,8=0,336.
7. Из 10 деталей 7 – стандартные. Наудачу берут 6 деталей. Найти вероятность того, что среди них: а) не более одной нестандартной; б) не более двух нестандартных.
Решение.
а). Обозначим события А – среди взятых 6 деталей нестандартных нет;
В – в 6 выбранных деталях одна нестандартная. Тогда А+В – среди 6 деталей не более одной нестандартной. Найдем Р(А+В). Заметим, что
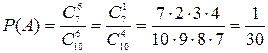 ,
,
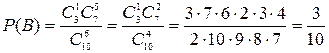 .
.
Откуда
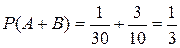 .
.
б). Пусть теперь событие А – в шести взятых деталях не более двух нестандартных. Тогда 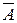 - в выбранных деталях более двух нестандартных, т.е. три.
- в выбранных деталях более двух нестандартных, т.е. три.
 .
.
 .
.
Формула полной вероятности
Пусть событие А может наступить при условии появления одного из несовместных событий В1, В2,…В n, которые образуют полную группу. Пусть известны вероятности этих событий и условные вероятности события А.
Теорема. Если событие А может произойти только при выполнении одного из событий В1, В2,…В n, которые образуют полную группу несовместных событий, то вероятность события А вычисляется по формуле
 .
.
Эта формула называется формулой полной вероятности.
Пример.
1. В урну, содержащую два шара, опущен белый шар, после чего из нее наудачу извлечен один шар. Найти вероятность того, ч то извлеченный шар окажется белым, если равно возможны все предположения о первоначальном составе шаров.
Решение:
Обозначим события: А – извлечен белый шар;
В1 – первоначально белых шаров в урне не было;
В2 – первоначально в урне был один белый шар;
В3 – первоначально в урне было два белых шара.
Заметим, что 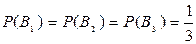 ,
,  ,
, 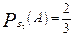 ,
,  . Тогда по формуле полной вероятности
. Тогда по формуле полной вероятности
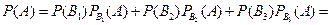
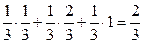 .
.
Формула Байеса
Вновь рассмотрим полную группу несовместных событий В1, В2,…В n вероятности появления которых 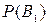 ,
, 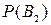 ,…,
,…, 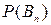 . Событие А может произойти только вместе с каким-либо из событий В1, В2,…В n, которые будем называть гипотезами. Тогда по формуле полной вероятности:
. Событие А может произойти только вместе с каким-либо из событий В1, В2,…В n, которые будем называть гипотезами. Тогда по формуле полной вероятности:
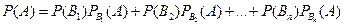 .
.
Если событие А произошло, то это может изменить вероятности гипотез 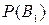 ,
,  ,…,
,…, 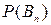 . По теореме умножения вероятностей
. По теореме умножения вероятностей
 ,
,
откуда: 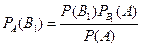 .
.
Аналогично, для остальных гипотез: 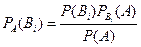 , i=1,2,…,n.
, i=1,2,…,n.
Полученная формула называется формулой Байеса. Здесь Р(А) определяется формулой полной вероятности.
Пример.
1. 30% приборов собирает специалист высокой квалификации и 70% специалист средней квалификации. Надежность работы прибора, собранного специалистом высокой квалификации, 0,9, надежность прибора, собранного специалистом средней квалификации, 0,8. Взятый прибор оказался надежным. Определить вероятность того, что он собран специалистом высокой квалификации.
Решение.
События: А – безотказная работа прибора;
В1 – прибор собран специалистом высокой квалификации;
В2 – прибор собран специалистом средней квалификации.
Выпишем вероятности гипотез:  ,
, 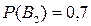 .
.
Условные вероятности события А: 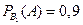 ,
,  .
.
Вероятность события А: 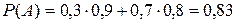 .
.
Определим вероятность гипотезы В1 при условии, что событие А произошло
 .
.
Примеры решения типовых задач
1. В пирамиде 5 винтовок, три из которых снабжены оптическим прицелом. Вероятность того, что стрелок поразит мишень при выстреле из винтовки с прицелом, равна 0,95, для винтовки без прицела соответствующая вероятность равна 0,7. Найти вероятность того, что мишень будет поражена, если стрелок делает один выстрел из произвольной винтовки.
Решение:
Пусть А–мишень поражена;
В1–произведен выстрел из винтовки с прицелом;
В1–выстрел из винтовки без прицела.
Тогда 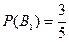 ,
,  и по формуле полной вероятности
и по формуле полной вероятности
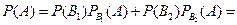
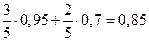 .
.
2. Батарея из трех орудий произвела залп, причем два снаряда попали в цель. Найти вероятность того, что первое орудие попало, если вероятности попадания в цель каждым из орудий равны р1=0,4, р2=0,3, р3=0,5.
Решение.
Обозначим события: А – два орудия попали в цель;
В1 – первое орудие попало в цель; В2 – первое орудие не попало в цель.
Вероятности гипотез: 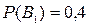 ,
, 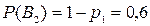 .
.
Условные вероятности события А:
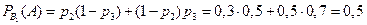 .
.
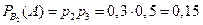 .
.
По формуле Байеса

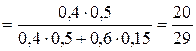 .
.
3. Три компьютерные фирмы представили в контрольное управление компьютеры для выборочной проверки: первая – 20 компьютеров; вторая – 30 компьютеров; третья – 50 компьютеров. Вероятности того, что компьютеры без брака у этих фирм соответственно равны: 0,8; 0,9; 0,7. Был выбран один компьютер, и он оказался без брака. Определить вероятность того, что этот компьютер принадлежит третьей фирме.
Решение.
Здесь события 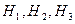 - это выбор компьютера соответственно у первой, второй и третьей фирмы. Вероятности этих событий таковы:
- это выбор компьютера соответственно у первой, второй и третьей фирмы. Вероятности этих событий таковы: 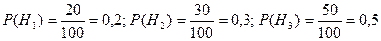 .
.
По формуле полной вероятности определяем вероятность выбора компьютера без брака (событие А): 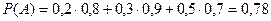 .
.
По формуле Байеса находим искомую вероятность:
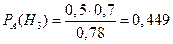 .
.
4. На сборку телевизоров поступают микросхемы от двух поставщиков, причем 70% микросхем от первого поставщика, 30% – от второго. Брак микросхем первого поставщика составляет 2%, второго – 3%. Взятая наудачу микросхема оказалась бракованной. Какова вероятность, что микросхема изготовлена первым поставщиком? Вторым поставщиком?
Решение.
Обозначим
 – взятая наудачу микросхема изготовлена первым поставщиком,
– взятая наудачу микросхема изготовлена первым поставщиком,
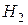 – взятая наудачу микросхема изготовлена вторым поставщиком,
– взятая наудачу микросхема изготовлена вторым поставщиком,
А – взятая наудачу микросхема дефектна – произошло в результате испытания.
Найдем вероятность того, что эта микросхема была изготовлена первым поставщиком по формуле Байеса:
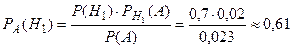 .
.
Аналогично, вероятность того, что микросхема была изготовлена вторым поставщиком:
 .
.
5. По цели произведено три последовательных выстрела. Вероятность попадания при первом выстреле р1=0,3, при втором р2=0,6, при третьем р3=0,8. При одном попадании вероятность поражения цели r1=0,4, при двух попаданиях r2=0,7, при трех попаданиях r3=1. Определить вероятность поражения цели при трех выстрелах.
Решение.
Рассмотрим полную группу несовместных событий:
В1 – было одно попадание;
В2 – было два попадания;
В3 – было три попадания;
В4 – не было ни одного попадания.
Определим вероятность каждого события. По теоремам умножения и сложения вероятностей будем иметь
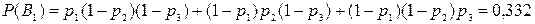 .
.
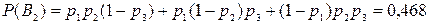 .
.
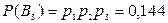 .
.
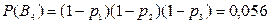 .
.
Пусть событие А – цель поражена. Выпишем условные вероятности поражения цели при осуществлении каждого из событий В1, В2, В3, и В4.
 ,
,  ,
, 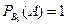 ,
, 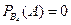 .
.
Тогда по формуле полной вероятности:
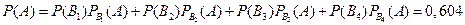
Решение:
Введем обозначения:
события А- поступившая деталь на сборку бракованная;В1 – детали с первого станка;
В2 – детали со второго станка;
В3 – детали с третьего станка;
В4 – детали с четвертого станка.
Воспользуемся формулой полной вероятности где P(B1)= 0,4 ; P(B2)= 0,3 ; P(B3)= 0,2 ; P(B4)= 0,1
где P(B1)= 0,4 ; P(B2)= 0,3 ; P(B3)= 0,2 ; P(B4)= 0,1 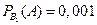 ,
, 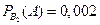 ,
, 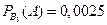 ,
, 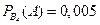 .
.
 7. Для участия в спортивных соревнованиях из 1-ой группы было выделено 4 студента; из 2-ой -6 ; из 3-й – 5 студентов. Вероятность того, что студент каждый из групп попадает в сборную института равны 0,5 ; 0,4; 0,3 соответственно для каждой из групп. Наудачу выбранный участник попал в сборную. К какой из 3-х групп он вероятнее всего принадлежит?Решение: Пусть событие А –произвольно выбранный студент попал в сборную . (Всего было студентов N=4+6+5=15).
7. Для участия в спортивных соревнованиях из 1-ой группы было выделено 4 студента; из 2-ой -6 ; из 3-й – 5 студентов. Вероятность того, что студент каждый из групп попадает в сборную института равны 0,5 ; 0,4; 0,3 соответственно для каждой из групп. Наудачу выбранный участник попал в сборную. К какой из 3-х групп он вероятнее всего принадлежит?Решение: Пусть событие А –произвольно выбранный студент попал в сборную . (Всего было студентов N=4+6+5=15). В1 –студент из первой группы;
В2 – студент из второй группы;
В3 - студент из третьей группы.
Вычислим вероятности того, что студент попавший в сборную принадлежит к той или иной из 3-х групп по формуле Бейеса: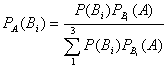 Вероятность принадлежности студента к каждой из групп равна::
Вероятность принадлежности студента к каждой из групп равна:: 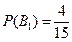 ;
; 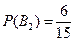 ;
; 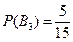 Условные вероятности события А:
Условные вероятности события А:  ,
, 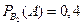
 .
. Вероятность события А:
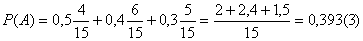
Определим вероятность гипотезы В1 при условии, что событие А произошло
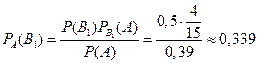 ;
;  ;
;
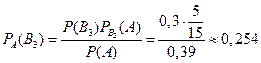
Формула Бернулли
Если производится n независимых испытаний, в каждом из которых вероятность появления события А одна и та же и равна р, то вероятность того, что событие А появится в этих n испытаниях k раз, выражается формулой
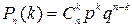 , где q=1-k.
, где q=1-k.
В частности, отсюда Р n(0)=qn, Р n(1)=npqn -1, … , Р n(n)=pn.
С помощью формулы Бернулли обычно вычисляются вероятности тех событий, которые происходят в небольшом числе опытов.
Следствия:
1). Вероятность того, что в n независимых испытаниях событие наступит не менее m1 раз и не более m2 раза, определится по формуле:
Рn(m1  m2)= Рn(m1) +...+ Рn(m2)=
m2)= Рn(m1) +...+ Рn(m2)= 
2). Вероятность того, что в n независимых испытаниях событие наступит хотя бы один раз, определится по формуле:
Рn( 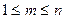 )=
)=  =1
=1
Примеры.
1. В урне 20 белых и 10 черных шаров. Вынули 4 шара, причем каждый вынутый шар возвращают в урну перед извлечением следующего и шары в урне перемешивают. Найти вероятность того, что из четырех вынутых шаров окажется 2 белых.
Решение:
Событие А – достали белый шар. Тогда вероятности 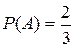 ,
, 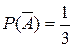 . По формуле Бернулли требуемая вероятность
. По формуле Бернулли требуемая вероятность
 .
.
2. Определить вероятность того, что в семье, имеющей 5 деталей, будет не больше трех девочек. Вероятности рождения мальчика и девочки предполагаются одинаковыми.
Решение:
Вероятность рождения девочки 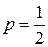 , тогда
, тогда 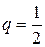 .
.
Найдем вероятности того, что в семье нет девочек, родилась одна, две или три девочки:
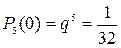 ,
,  ,
,
 ,
, 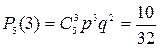 .
.
Следовательно, искомая вероятность
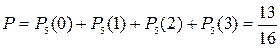 .
.
3. По цели производится 5 выстрелов. Вероятность попадания для каждого выстрела равна 0,4. Найти вероятность того, что в цель попали не менее трех раз.
Решение:
Вероятность не менее трех попаданий складывается из вероятности пяти попаданий, четырех попаданий и трех попаданий.
Т.к. выстрелы независимы, то можно применить формулу Бернулли вероятности того, что в п испытаниях событие с вероятностью р наступает ровно т раз.
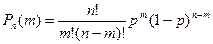
В случае пяти попаданий из пяти возможных: 
Четыре попадания из пяти выстрелов: 
Три попадания из пяти: 
Окончательно, получаем вероятность не менее трех попаданий из пяти выстрелов:
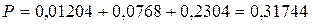
4. Всхожесть семян некоторой культуры 90%. Найти вероятность того, что из 10 случайно отобранных семян взойдет не менее 8.
Решение:
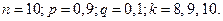
Так как проводится п независимых испытаний и п невелико, то применяем формулу Бернулли:
 .
.
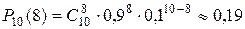
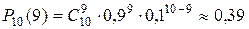 .
.
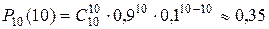 .
.
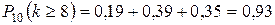 .
.
Примеры.
1. Вероятность получения с конвейера изделий первого сорта равна 0,9. Определить вероятность того, что из взятых на проверку 600 изделий 530 будут первого сорта.
Решение:
n =600, m =530, р=0,9, q=1-0,9=0,1 Вычислим значение х:
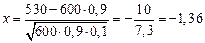
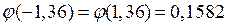
Р600(530)= 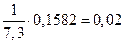
2. Вероятность того что деталь не прошла проверку равна 0,2. Найти вероятность того что среди 400 случайно отобранных деталей окажется непроверенных больше 100 деталей.
Решение:
n=400, m1=100, m2=400 p=0,2, q=0,8.
х¢ =  х² =
х² = 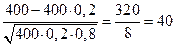
Ф(х¢)= 0,4938, Ф(х²)=0,5 Р(100 £m£ 400)=0,4938+0,5=0,9938
Формула Пуассона
При большом числе испытаний n и малой вероятности р формулой Бернулли пользоваться неудобно, например, 0,951000 вычислить трудно. В этом случае для вычисления вероятности того, что в n испытаниях (n – велико) событие произойдет m раз используют формулу Пуассона
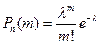 ,
,
где λ=np=const – среднее число появлений события в n испытаниях.
Примеры.
1. Устройство состоит из 1000 элементов, работающих независимо один от другого. Вероятность отказа любого элемента в течении времени Т равна 0,002. Найти вероятность того, что за время Т откажут ровно три элемента.
Решение:
n=1000, p=0,002, λ=np=2, m=3.
Искомая вероятность 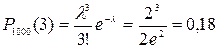 .
.
2. Завод отправил на базу 500 изделий. Вероятность повреждения изделия в пути 0,004. Найти вероятность того, что в пути повреждено меньше трех изделий.
Решение:
n=500, p=0,004, λ=2.
По теореме сложения вероятностей
 .
.
3. Магазин получил 1000 бутылок минеральной воды. Вероятность того, что при перевозке бутылка окажется разбитой, равна 0,003. Найти вероятность того, что магазин получит более двух разбитых бутылок.
Решение:
По формуле Пуассона:
λ=np=1000·0,003=3
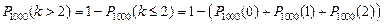

Примеры решения типовых задач
1. В жилом доме имеется 6400 ламп, вероятность включения каждой из них в вечернее время равна 0,5. Найти вероятность того, что число одновременно включенных ламп будет между 3120 и 3200.
Решение:
Используем интегральную теорему Лапласа, где n = 6400, p = 0,5, q = 1-p = 0,5, m1 =3120, m2 = 3200.
 .
.
 ;
;  .
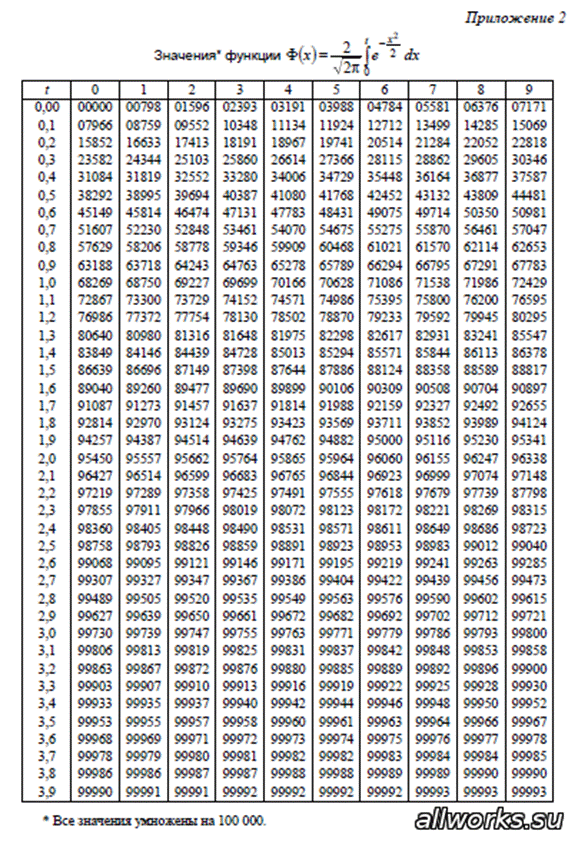
.
Находим по таблице приложения 2:

Тогда 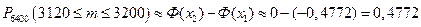 .
.
2. Вычислительное устройство состоит из 1000 элементов, работающих независимо друг от друга. Вероятность отказа каждого элемента за смену равна 0,024. Найти вероятность, что за смену откажут 6 элементов.
Решение:
Используем локальную теорему Лапласа:
n =1000, m =6, р=0,024, q=1-0,024=0,976.
Вычислим значение х:

Найдем по таблице приложения 1:

Р1000(6)= 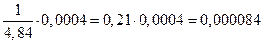
3. Найти вероятность того, что если бросить монету 200 раз, то орел выпадет от 90 до 110 раз.
Решение:
Так как число n=200 достаточно велико, будем использовать интегральную теорему Лапласа для подсчета вероятности, где m1 =90, m2 = 110, вероятность появления орла равна р = 0,5, и не появления q=0,5.
 . .
 . .  .
Находим по таблице приложения 2: .
Находим по таблице приложения 2:
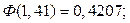  Тогда
Тогда  . .
|
4. Всхожесть семян некоторой культуры 90%. Найти вероятности следующих событий: а) из 100 семян взойдет ровно 80 семян; б) из 100 семян взойдет не менее 70 семян и не более 95 семян.
Решение.
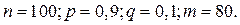
Так как п–велико, то применяем локальную формулу Муавра-Лапласа:
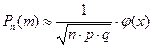 , где
, где 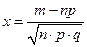 ,
,
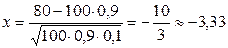 ,
, 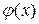 – четная функция,
– четная функция, 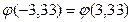 .
.
Находим по таблице приложения 1 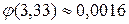 .
.
Тогда  .
.
Так как полученная вероятность очень мала, то событие, что из 100 семян взойдет ровно 80, практически невозможно.
б) 
Так как n большое и m принимает целые значения из промежутка 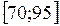 , то применяем интегральную формулу Муавра-Лапласа.
, то применяем интегральную формулу Муавра-Лапласа.
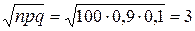 .
.
 .
. 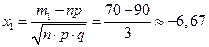 .
.
Находим по таблице приложения 2:
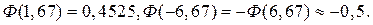
Тогда  .
.
5. Найти вероятность того, что событие А наступит ровно 80 раз при 400 испытаниях, если вероятность появления этого события в каждом испытании равна 0,2.
Решение:
По условию n =400, m=80, p=0,2, q=0,8.
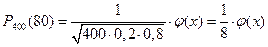
х= 
По таблице приложения 1 находим что φ(0)=0,04986
Тогда Р400(80)= 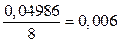 .
.
Основные понятия случайных величин
Определение. Случайной называется величина, которая в результате испытания принимает одно и только одно возможное значение, какое именно заранее неизвестно.
Случайные величины делятся на дискретные и непрерывные.
Определение. Случайная величина называется дискретной, если в результате испытания она принимает одно из значений х1, х2, х3, … , х n, … с соответствующей вероятностью р1, р2, … , р n, …
Определение. Непрерывной называется случайная величина, которая может принимать любое значение из некоторого промежутка.
Например, число студентов на лекции – дискретная случайная величина, продолжительность лекции – непрерывная.
Закон распределения дискретной случайной величины
Соответствие между возможными значениями х k случайной величины Х и их вероятностями р k называется законом распределения вероятностей дискретной случайной величины Х.
Закон распределения обычно задается таблицей:
| Возможные значения случайной величины Х | х1 | х2 | … | хn |
| Вероятности этих значений Р | р1 | р2 | … | рn |
То, что случайная величина Х принимает одно из значений х1, х2, … , х n, есть достоверное событие и поэтому должно выполняться равенство 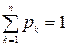 (в случае бесконечной последовательности значений
(в случае бесконечной последовательности значений 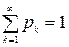 ).
).
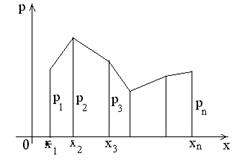
Закон распределения может быть задан графически в виде многоугольника распределения вероятностей, т.е. в виде ломаной, соединяющей точки (х k, р k).
Примеры.
1. Переменная величина Х есть число очков, выпадающее на верхней грани игральной кости при ее однократном бросании. Составить закон распределения этой случайной величины.
Решение.
Так как любое число очков при однократном бросании кости выпадает с вероятностью 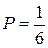 , то закон распределения случайной величины имеет вид:
, то закон распределения случайной величины имеет вид:
| Х | 1 | 2 | 3 | 4 | 5 | 6 |
| р | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 |
2. Вероятность попадания при каждом выстреле р=0,8. Имеется три снаряда. Определить вероятность того, что будет израсходован один снаряд, два снаряда, три снаряда, если стрельба ведется до первого попадания или промаха всеми тремя снарядами. Составить таблицу распределения случайной величины Х – числа израсходованных снарядов.
Решение.
Пусть Х – число израсходованных снарядов. Обозначим  - вероятность того, что будет израсходовано х k снарядов.
- вероятность того, что будет израсходовано х k снарядов.
Тогда Р(х=1)=0,8, Р(х=2)=(1-р)р=0,16, Р(х=3)=(1-р)2=0,04.
Таблица распределения будет иметь вид
| Х | 1 | 2 | 3 |
| р | 0,8 | 0,16 | 0,04 |
3. Экзаменатор задал студенту 4 дополнительных вопроса. Вероятность того, что студент ответит на любой заданный вопрос 0,9. Составить закон распределения случайной величины Х – числа ответов на заданные вопросы.
Решение.
Используем формулу Бернулли  . Здесь n=4, р=0,9, q=0,1.
. Здесь n=4, р=0,9, q=0,1.
 ,
,
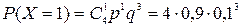 ,
,
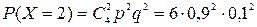 ,
,
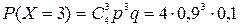 ,
,
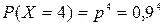 .
.
| Х | 0 | 1 | 2 | 3 | 4 |
| Р | 0,0001 | 0,0036 | 0,0486 | 0,2916 | 0,6561 |
Свойства дисперсии
1. D[C]=0, где С=const.
2. D[CX]=C2·D[X].
3. Для независимых случайных величин Х и У D[X + Y]= D[X] + D[Y].
Примеры решения типовых задач
1. Случайная величина Х задана следующим законом распределения:
| Х | 2 | 3 | 4 |
| р | 0,3 | 0,4 | 0,3 |
Найдем ее математическое ожидание, дисперсию и среднеквадратичное отклонение.
Решение:
M[X]=2·0,3+3·0,4+4·0,3=3;
D[X]=(2 – 3)2·0,3+(3 – 3)2·0,4+(4 – 3)2·0,3=0,6;
 .
.
2. Независимые дискретные величины X и Y заданы законами распределения: Найти математическое ожидание, дисперсию и среднее квадратическое отклонение для случайной величины Z .
| Х | –1 | 0 | 1 |
| Y | –2 | 0 |
| р | 0,2 | 0,3 | 0,5 | р | 0,3 | 0,7 |

Решение:
Используя свойства математического ожидания
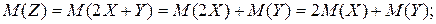
Найдем математическое ожидание Z:
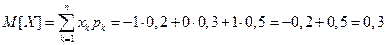
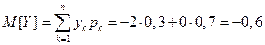
Подставляя в формулу найденные значения М(Х) и М(Y)
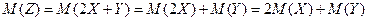
получим:
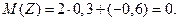
Используя свойства дисперсии, получим:
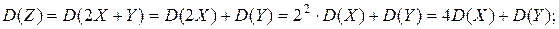
Найдем дисперсию по формуле:
D[X]= M[X2] – (M[X])2.
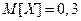
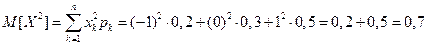
Тогда 
Аналогично посчитаем: D[Y]= M[Y2] – (M[Y])2.

Найдем среднее квадратическое отклонение по формуле:
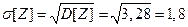
Пример.
Случайная величина Х задана плотностью распределения
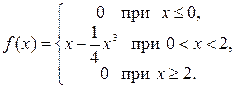
Найти математическое ожидание, дисперсию и среднеквадратичное отклонение величины Х.
Воспользуемся определениями.
 .
.
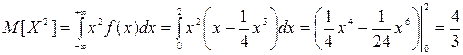 .
.
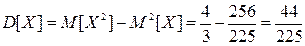 .
.
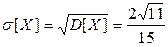 .
.
Примеры решения типовых задач
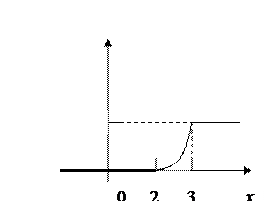
1. Случайная величина X задана функцией распределения вероятностей F(x). Найти: а) плотность распределения вероятностей случайной величины X; б) вероятность попадания случайной величины в интервал (1; 2,5); Построить графики функции и плотности распределения случайной величины Х.
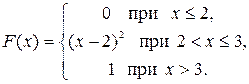
Решение
а). По определению

б). Требуемая вероятность будет
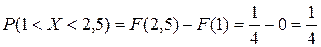 .
. 
Глава 7. Выборочный метод
Способы составления выборки
1) простой (случайный) – отбор, при котором объекты извлекают по одному из всей генеральной совокупности;
2) механический – отбор, при котором генеральную совокупность «механически» делят на столько групп, сколько объектов должно войти в выборку, а из каждой группы отбирают один объект.
Например, если нужно отобрать 20% готовых деталей, то отбирают каждую 5-ую деталь, а если 5% -то каждую двадцатую.
3.) типический - отбор при котором объекты отбираются не из всей генеральной совокупности, а из каждой ее «типической» части.
Например, если деталь изготавливают на нескольких станках, то отбор производят не из всей совокупности деталей, произведенных всеми станками, а из продукции каждого станка в отдельности.
СТАТИСТИЧЕСКИХ ГИПОТЕЗ
Глава 9. Проверка гипотез
Пример решения типовой задачи
Комитетом по физической культуре и спорту были проведены исследования спортсменов, занимающихся стрельбой. Было отобрано 200 стрелков из 4000 для определения среднего количества патронов, необходимых одному спортсмену для одной тренировки. Результаты обследования приведены в таблице
| Число патронов (шт.) | Менее 200 | 200-300 | 300-400 | 400-500 | 500-600 | 600-700 | Более 700 |
| Число спортсменов (чел.) | 4 | 20 | 57 | 65 | 31 | 15 | 8 |
1. Перейти к вариационному ряду, и построить полигон частот.
2. Найти выборочную среднюю, выборочную дисперсию, исправленную выборочную дисперсию, исправленное выборочное среднеквадратическое отклонение случайной величины Х.
3. Построить доверительный интервал для генеральной средней и генерального среднеквадратического отклонения с заданным уровнем доверительной вероятности γ=0,95.
4. Используя критерий 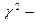 Пирсона при уровне значимости a=0,05 проверить гипотезу о том, что случайная величина X– распределена по нормальному закону. Построить на одном графике гистограмму эмпирического распределения и соответствующую нормальную кривую.
Пирсона при уровне значимости a=0,05 проверить гипотезу о том, что случайная величина X– распределена по нормальному закону. Построить на одном графике гистограмму эмпирического распределения и соответствующую нормальную кривую.
Решение.
1. Перейдем от данного интервального ряда к вариационному. Для этого найдем середину каждого интервала (сложим концы каждого интервала и поделим пополам):
| Число патронов (шт.), х i | 150 | 250 | 350 | 450 | 550 | 650 | 750 |
| Число спортсменов (чел.), ni | 4 | 20 | 57 | 65 | 31 | 15 | 8 |
Построим полигон частот для полученного вариационного ряда.
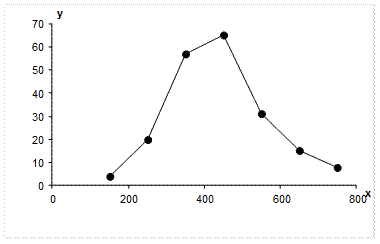
2. Находим выборочную среднюю по формуле:
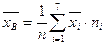 .
.
Объем выборки n=200.
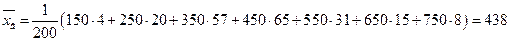
Таким образом, среднее число патронов необходимых одному спортсмену для одной тренировки равно 438 шт.
Находим выборочную дисперсию:
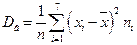 = 16656
= 16656
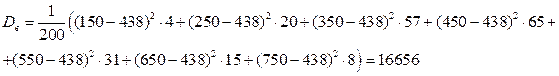
Посчитаем выборочную дисперсию вторым способом:
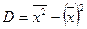 , где
, где 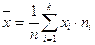 и
и 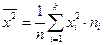 .
.
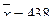
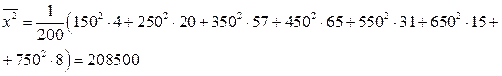
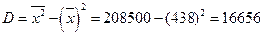
Среднеквадратическое отклонение: 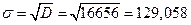
Исправленную выборочную дисперсию посчитаем по формуле:
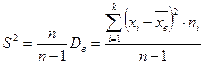
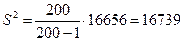
Исправленное выборочное среднеквадратическое отклонение случайной величины Х :
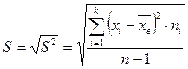

3. Построить доверительный интервал для генеральной средней и генерального среднеквадратического отклонения с заданным уровнем доверительной вероятности γ=0,95. Тем самым, найдем границы, в которых с вероятностью 0,95 заключено среднее число патронов, необходимых для тренировки одного спортсмена.
Доверительный интервал для генеральной средней находим по формуле:
 , где
, где 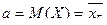 - математическое ожидание;
- математическое ожидание;
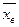 - выборочная средняя;
- выборочная средняя;
 - объем выборки;
- объем выборки;
 - при большом объеме выборки;
- при большом объеме выборки;
t- значение аргумента функции Лапласа, при котором она равна 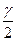 , то есть
, то есть 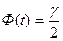 , где
, где 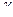 - заданная надежность. Аргумент t находится по таблицам значений функции Лапласа (приложение 2). По таблицам значений функции Лапласа находим: Ф(t)=0,95
- заданная надежность. Аргумент t находится по таблицам значений функции Лапласа (приложение 2). По таблицам значений функции Лапласа находим: Ф(t)=0,95 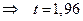 .
.

 ;
; 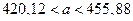
Доверительный интервал для оценки среднеквадратического отклонения  вычисляется по формуле
вычисляется по формуле
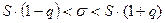 ,
,
где 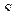 - это исправленное среднеквадратическое отклонение;
- это исправленное среднеквадратическое отклонение;
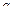 - это табличное значение, которое зависит от объема выборки
- это табличное значение, которое зависит от объема выборки  и заданной надежности
и заданной надежности 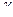 , то есть
, то есть 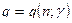 (приложение 4).
(приложение 4).
Найдем значение q: 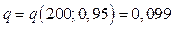
Тогда доверительный интервал для оценки среднеквадратического отклонения  будет равен:
будет равен:
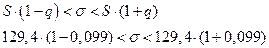
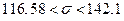
4. Используя критерий 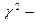 Пирсона при уровне значимости a=0,05 проверим гипотезу о том, что случайная величина X– распределена по нормальному закону.
Пирсона при уровне значимости a=0,05 проверим гипотезу о том, что случайная величина X– распределена по нормальному закону.
Примечание: В качестве дисперсии нормального закона распределения следует взять исправленную выборочную дисперсию. Но т.к. количество наблюдений – 200 достаточно велико, то подойдет и “обычная”  .
.
| xi | ni | 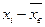
| 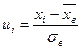
| 
| 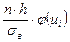
| 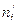
|
| 150 | 4 | -288 | -2,23 | 0,0332 | 5,144974 | 5,1 |
| 250 | 20 | -188 | -1,46 | 0,1374 | 21,29275 | 21,3 |
| 350 | 57 | -88 | -0,68 | 0,3166 | 49,06321 | 49,1 |
| 450 | 65 | 12 | 0,09 | 0,3973 | 61,56922 | 61,6 |
| 550 | 31 | 112 | 0,87 | 0,2732 | 42,33755 | 42,3 |
| 650 | 15 | 212 | 1,64 | 0,1040 | 16,11678 | 16,1 |
| 750 | 8 | 312 | 2,42 | 0,0213 | 3,300841 | 3,3 |
| 200 | 198,8 |
Составим расчетную таблицу для вычисления теоретических частот пользуюсь указанной схемой.
Для этого найдем величину
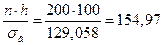 .(h-длина интервала или шаг).
.(h-длина интервала или шаг).
Из первого пункта данной задачи известно, что 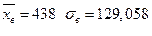 .
.
Составим таблицу для подсчета 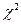
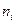
| 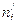
| 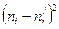
| 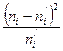
|
| 4 | 5,1 | 1,21 | 0,237255 |
| 20 | 21,3 | 1,69 | 0,079343 |
| 57 | 49,1 | 62,41 | 1,271079 |
| 65 | 61,6 | 11,56 | 0,187662 |
| 31 | 42,3 | 127,69 | 3,018676 |
| 15 | 16,1 | 1,21 | 0,075155 |
| 8 | 3,3 | 22,09 | 6,693939 |
| 200 | 198,8 | 11,56311 |
Итого, значение статистики  .
.
Определим количество степеней свободы по формуле: 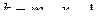 .
.
m–число интервалов (m=7), r – число параметров закона распределения (в нормальном распределении r = 2)
Т.е. k = 7-2-1=4.
Соответствующее критическое значение статистики 
Поскольку  , гипотеза о нормальном распределении с параметрами N(438; 129,058) не согласуется с опытными данными.
, гипотеза о нормальном распределении с параметрами N(438; 129,058) не согласуется с опытными данными.
Ниже показана кривая эмпирического (сплошная линия) и теоретического (пунктирная линия) распределений

Вывод. Сопоставив обе кривых видим, что наилучшее соответствие эмпирических данных нормальному распределению наблюдается на первом, втором, и шестом интервалах, что подтверждается таблицей. А вот на участке от 500 до 600 патронов отклонение очень большое – это видно из графика. Оно и оказало “фатальное” влияние на критерий согласия – это видно из таблицы.
Основные понятия корреляционного анализа.
Во многих задачах требуется установить зависимость изучаемой случайной величины  от одной или нескольких случайных величин. Рассмотрим зависимость случайной величины
от одной или нескольких случайных величин. Рассмотрим зависимость случайной величины  от одной случайной (или неслучайной) величины
от одной случайной (или неслучайной) величины  .
.
Две случайные величины могут быть связаны между собой либо функциональной зависимостью, либо статистической, либо быть независимыми.
Определение . Функциональной называют зависимость, при которой каждому возможному значению случайной величины 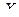 соответствует одно возможное значение случайной величины
соответствует одно возможное значение случайной величины  и обозначают
и обозначают
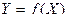 .
.
Строгая функциональная зависимость реализуется редко, так как обе величины или одна из них подвержены еще воздействию случайных факторов, причем среди них могут быть и общие для обеих случайных величин факторы. Такую зависимость называют статистической.
Определение . Статистической называется зависимость, при которой изменение одной случайной величины влечет изменение закона распределения другой случайной величины.
Определение . Статистическая зависимость называется корреляционной, если при изменении одной случайной величины изменяется среднее значение другой.
Пример. Пусть случайная величина  - это количество внесенных удобрений, а
- это количество внесенных удобрений, а  - это урожайность зерна. Как показывает практика, между этими величинами нет функциональной связи, так как урожайность может зависеть и от других факторов (осадки, температура воздуха и др.), поэтому, от количества внесенных удобрений зависит только средняя урожайность, следовательно связь между случайными величинами
- это урожайность зерна. Как показывает практика, между этими величинами нет функциональной связи, так как урожайность может зависеть и от других факторов (осадки, температура воздуха и др.), поэтому, от количества внесенных удобрений зависит только средняя урожайность, следовательно связь между случайными величинами 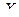 и
и  является корреляционной.
является корреляционной.
Таким образом, в основе корреляционного анализа лежит соотношение, существующее между значением одной случайной величины и средним значением другой.
Задача установления корреляционной связи распадается на две задачи. Первая состоит в установлении формы связи, то есть в определении вида функции, связывающей значения одной случайной величины со средним значением другой. Вторая задача состоит в оценке силы (тесноты) корреляционной связи. Рассмотрим каждую из этих задач.
10.2. Корреляционная таблица и корреляционное поле
Для установления формы связи между случайными величинами 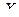 и
и  строят корреляционную таблицу, а затем корреляционное поле.
строят корреляционную таблицу, а затем корреляционное поле.
Пусть при выборе объема 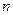 некоторое значение
некоторое значение 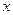 встречалось
встречалось 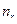 раз, некоторое значение
раз, некоторое значение 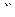 встречалось
встречалось  раз, и одна и та же пара чисел пара чисел
раз, и одна и та же пара чисел пара чисел 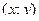 встречалась
встречалась 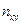 раз. Полученные данные удобно группировать в виде таблицы, которую называют корреляционной таблицей.
раз. Полученные данные удобно группировать в виде таблицы, которую называют корреляционной таблицей.
Поясним устройство корреляционной таблицы на примере.
Пример. Пусть  - это прибыль предприятия в год (млн. руб.);
- это прибыль предприятия в год (млн. руб.); 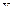 - это фонд материального поощрения (% от прибыли).
- это фонд материального поощрения (% от прибыли).
| x y | 10 | 20 | 30 | 40 | ny |
| 5 | 5 | 7 | 14 | 26 | |
| 10 | 2 | 6 | 4 | 12 | |
| 15 | 3 | 19 | 22 | ||
| nx | 8 | 21 | 13 | 18 | 60 |
В первой строке таблицы указаны наблюдаемые значения прибыли предприятия, а в первом столбце – процент от прибыли в фонд материального поощрения работников. На пересечении строк и столбцов находятся частоты  наблюдаемых пар значений
наблюдаемых пар значений 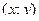 , например, пара (10;5) – встречалась на 5-ти предприятиях, а пара (30;15) – не встречалась не одного раза.
, например, пара (10;5) – встречалась на 5-ти предприятиях, а пара (30;15) – не встречалась не одного раза.
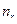 - это частота повторений значений
- это частота повторений значений 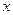 признака
признака 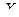 , равная сумме всех частот столбца, и указывающая, сколько раз всего встречалось данное значение
, равная сумме всех частот столбца, и указывающая, сколько раз всего встречалось данное значение 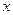 , например,
, например, 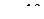 встречалось 8 раз.
встречалось 8 раз.
 - частота повторений значений
- частота повторений значений 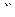 признака
признака 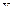 , равная сумме всех частот по строке и указывающая, сколько раз встречалось значение
, равная сумме всех частот по строке и указывающая, сколько раз встречалось значение 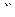 , например, значение
, например, значение 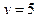 встречалось 26 раз.
встречалось 26 раз.
В правом нижнем углу таблицы указывается объем выборки 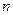 , равный сумме всех частот по строке (и по столбцу), то есть
, равный сумме всех частот по строке (и по столбцу), то есть
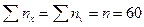 .
.
Таким образом выборка проведена по 60-ти предприятиям.
После того, как данные сгруппированы в виде корреляционной таблицы, строят корреляционное поле. Для этого в прямоугольной системе координат отмечают точки с координатами 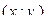 , то есть пары наблюдаемых значений величин
, то есть пары наблюдаемых значений величин  и
и 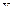 . По разбросу точек предполагают, какой именно можно считать связь между признаками, то есть с помощью какой функции ее можно описать.
. По разбросу точек предполагают, какой именно можно считать связь между признаками, то есть с помощью какой функции ее можно описать.
Пример. Построим корреляционное поле для предыдущего примера.
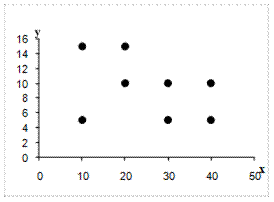
В данном примере связь предположительно можно считать линейной, так как все точки корреляционного поля располагаются в близи некоторой прямой линии.
Оценка тесноты любой связи
Как рассматривалось выше, оценка тесноты линейной связи осуществляется с помощью выборочного коэффициента корреляции. Но связь между признаками  и
и  не всегда является линейной. Рассмотрим, как оценить тесноту любой корреляционной связи, как линейной, так и нелинейной.
не всегда является линейной. Рассмотрим, как оценить тесноту любой корреляционной связи, как линейной, так и нелинейной.
Пусть данные наблюдений над количественными признаками  и
и  сведены в корреляционной таблице. Эти данные можно разбить на группы, причем каждая группа будет содержать те значения
сведены в корреляционной таблице. Эти данные можно разбить на группы, причем каждая группа будет содержать те значения  , которые соответствуют определенному значению
, которые соответствуют определенному значению  .
.
Пример. Пусть дана следующая корреляционная таблица
| x y | 2 | 3 | 5 | ny |
| 25 | 20 | 20 | ||
| 45 | 30 | 1 | 31 | |
| 110 | 1 | 48 | 49 | |
| nx | 20 | 31 | 49 | 100 |
Данные этой таблиц можно разбить на группы относительно признаков  и
и  . Рассмотрим группы по признаку
. Рассмотрим группы по признаку  .
.
К первой группе относится 20 значений 
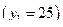 , которые соответствуют
, которые соответствуют 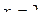 .
.
Ко второй группе относится 31 значений 
 , которые соответствуют
, которые соответствуют  .
.
К третей группе относится 49 значений 
 , которые соответствуют
, которые соответствуют 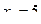 .
.
Таким образом, в данном случае, все исходные значения по признаку  , можно разбить на три группы и вычислить групповые средние, которые совпадают с условными средними:
, можно разбить на три группы и вычислить групповые средние, которые совпадают с условными средними:
 ;
; 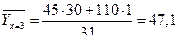 ;
;  .
.
Аналогично, можно разбить данные по признаку 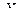 так же на три группы и найти групповые средние
так же на три группы и найти групповые средние 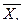 , получим
, получим
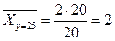 ;
; 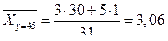 ;
; 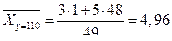 .
.
После разбиения данных на группы и вычисления групповых средних можно вычислить средние квадратические отклонения условных средних 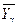 и
и 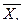 по формулам
по формулам 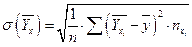 ,
, 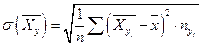 .
.
С помощью этих средних квадратических отклонений, вычисляют корреляционные отношения  по
по 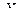 и
и  по
по  , по формулам
, по формулам
 и
и 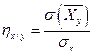 ,
,
где 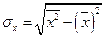 - среднее квадратическое отклонение признака
- среднее квадратическое отклонение признака  ;
;
 - среднее квадратическое отклонение признака
- среднее квадратическое отклонение признака  .
.
По приведенным корреляционным отношениям определяют тесноту любой связи, как линейной, так и нелинейной.
Пример решения типовой задачи
В таблице представлено распределение 200 драгоценных изделий по количеству примесей в них Х (%) и стоимости Y (тыс. руб):
| Х \ У | 3-9 | 9-15 | 15-21 | 21-27 | 27-33 | Более 33 | итого |
| 20-30 | 2 | 5 | 2 | 9 | |||
| 30-40 | 4 | 8 | 4 | 3 | 19 | ||
| 40-50 | 4 | 10 | 20 | 10 | 44 | ||
| 50-60 | 5 | 36 | 23 | 6 | 70 | ||
| 60-70 | 12 | 11 | 11 | 34 | |||
| 70-80 | 6 | 10 | 16 | ||||
| 80-90 | 8 | 8 | |||||
| Итого | 14 | 27 | 55 | 54 | 35 | 15 | 200 |
Необходимо:
1. Вычислить условные средние 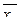 и
и 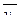 и построить эмпирические линии регрессии.
и построить эмпирические линии регрессии.
2. предполагая, что между переменными Х и Y существует линейная корреляционная зависимость:
а) найти уравнения прямых регрессии и построить их графики на одном чертеже с эмпирическими линиями регрессии;
б) вычислить коэффициент корреляции на уровне значимости 0,05, оценить его значимость и сделать вывод о тесноте и направлении связи между переменными Х и Y;
Решение:
Найдем условные средние по формулам
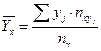 и
и 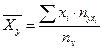 .
.
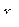 ,
, 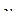 - середины соответствующих интервалов.
- середины соответствующих интервалов.
Найдем середины интервалов и запишем в таблицу:
| Х \ У | 6 | 12 | 18 | 24 | 30 | 36 | итого |
| 25 | 2 | 5 | 2 | 9 | |||
| 35 | 4 | 8 | 4 | 3 | 19 | ||
| 45 | 4 | 10 | 20 | 10 | 44 | ||
| 55 | 5 | 36 | 23 | 6 | 70 | ||
| 65 | 12 | 11 | 11 | 34 | |||
| 75 | 6 | 10 | 16 | ||||
| 85 | 8 | 8 | |||||
| Итого | 14 | 27 | 55 | 54 | 35 | 15 | 200 |
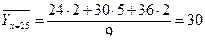


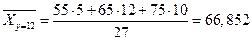


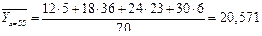
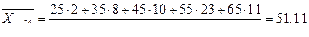


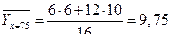

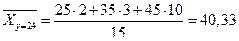
2а). Для нахождения уравнений регрессии вычисляем необходимые суммы. Для удобства их вычислений составим расчетные таблицы.
| 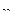
| 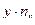
| 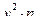
| 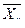
| 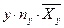
|
| 6 | 14 | 84 | 504 | 80,714 | 6778,8 |
| 12 | 27 | 324 | 3888 | 66,852 | 21675,6 |
| 18 | 55 | 990 | 17820 | 54,812 | 54261,9 |
| 24 | 54 | 1296 | 31104 | 51,11 | 66238,56 |
| 30 | 35 | 1050 | 31500 | 42,714 | 44847,6 |
| 36 | 15 | 540 | 19440 | 40,33 | 21778,2 |
| ∑ | 4284 | 104256 | - | 215580 |
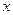
| 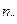
| 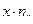
| 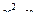
| 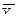
| 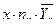
|
| 25 | 9 | 225 | 5625 | 30 | 6750 |
| 35 | 19 | 665 | 23275 | 25,895 | 17223,5 |
| 45 | 44 | 1980 | 89100 | 28,909 | 57239,82 |
| 55 | 70 | 3850 | 211750 | 20,571 | 79198,35 |
| 65 | 34 | 2210 | 143650 | 17,823 | 39388,83 |
| 75 | 16 | 1200 | 90000 | 9,75 | 11700 |
| 85 | 8 | 680 | 57800 | 6 | 4080 |
| ∑ | 10810 | 621200 | - | 215580 |

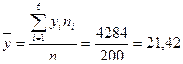
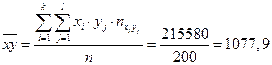


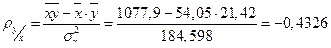
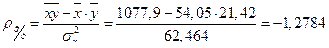
Тогда уравнение линейной регрессии у на х, будет иметь вид
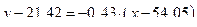 ,
,
или 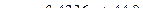
Тогда уравнение линейной регрессии х на у, будет иметь вид
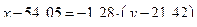 ,
,
или 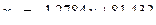
Ниже представлены графики полученных уравнений регрессии совместно с соответствующей эмпирической регрессией
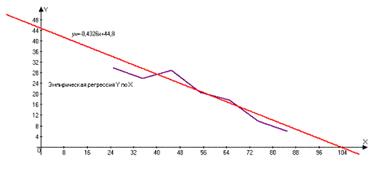

2б). Находим коэффициент корреляции 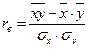
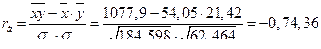
Так как 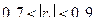 , то связь между рассматриваемыми признаками высокая, и так как
, то связь между рассматриваемыми признаками высокая, и так как  , то связь обратная.
, то связь обратная.
Проверим гипотезу о значимости коэффициента корреляции, то есть проверим гипотезу 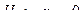 и
и
 .
.
Воспользуемся t - критерием Стьюдента, найдем 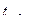 и
и 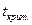 :
:
 .
.
Так как 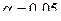 ,
, 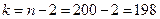 , то
, то
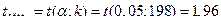 .
.
Таким образом, так как  , то коэффициент корреляции значимо отличается от нуля. Связь тесная и обратная.
, то коэффициент корреляции значимо отличается от нуля. Связь тесная и обратная.
2в). Для нахождения корреляционных отношений найдем средние квадратические отклонения для условных средних 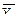 и
и 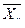 по формулам
по формулам
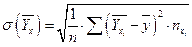 ,
,
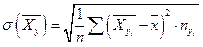 .
.
Получим
 ;
;
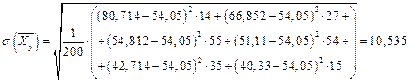 .
.
Тогда  ;
; 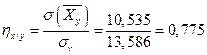 .
.
Корреляционное отношение 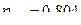 показывает, что признак
показывает, что признак  зависит от влияния признака
зависит от влияния признака 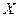 , а отношение
, а отношение 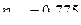 показывает, что признак
показывает, что признак 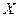 зависит от влияния признака
зависит от влияния признака  .
.
Процедура оценивания зачета
Очная форма обучения
Согласно положению о текущем контроле и промежуточной аттестации студентов, ФГБОУ ВО «Государственный аграрный университет Северного Зауралья» принятого решением ученого совета от 4 апреля 2016 г. протокол № 10: «зачет служит формой аттестации по итогам выполнения и защиты студентами лабораторных и практических занятий. При условии успешной защиты всех лабораторных работ и практических занятий, предусмотренных рабочей программой дисциплины, выставляется оценка «Зачтено»».
Таким образом, по дисциплине «Математика» выставляется оценка «Зачтено», при условии посещения студентами занятий; успешного выполнения контрольных работ; защиты РГР; получения положительной оценки при собеседовании по темам, выносимым на самостоятельное обучение.
Если студент не выполнил условия программы дисциплины, то зачет проводится в форме теста, по результатам которого выставляется оценка «Зачтено» либо «Не зачтено» в зависимости от процента верно выполненных заданий. Метод тестирования - бумажный. Перед началом работы над тестами преподаватель проводит инструктаж, разъясняет порядок заполнения ответов, порядок проведения тестирования, оговаривает вопросы соблюдения дисциплины при тестировании.
Время начала и окончания тестирования фиксируется, нарушение временного регламента не допускается.
Во время проведения тестирования каждому студенту предоставляется отдельное место, которое организуется в соответствии с требованиями гарантированного индивидуального выполнения теста.
При неоднократном нарушении дисциплины тестируемый удаляется из аудитории.
В процессе прохождения тестирования студенту разрешается пользоваться только ручкой, калькулятором и тестовыми материалами.
Заочная форма обучения
По дисциплине «Математика» студенты заочной формы в третьем семестре сдают зачет. Зачет выставляется по результатам РГР, которая предусмотрена учебным планом при посещении всех лекционных и практических занятий. В противном случае, процедура сдачи зачета как у студентов очного отделения.
Критерии оценки
Студенту выдается вариант с зачетными тестовыми заданиями и предоставляется 60 минут на подготовку. В задание включено 40 тестовых вопросов по 8 из каждой темы, с возможными вариантами ответов, из которых необходимо выбрать правильный. Оценка выставляется:
«зачтено», если студент верно отвечает на 60-100% вопросов теста.
«не зачтено», если обучающийся допустил грубые ошибки и ответил верно менее чем на 60% вопросов теста.
Учебно-методическое и информационное обеспечение дисциплины
а) основная литература
2. Гмурман В.Е. Теория вероятностей и математическая статистика: Учеб. пособие / В.Е. Гмурман. – М.: Высшее образование, 2006 г
3. Гмурман В.Е. Руководство к решению задач по теори вероятностей и математической статистике: Учеб. пособие / В.Е. Гмурман. – М.: Высшее образование, 2006 г.
4. Соколов, Г.А., Гладких. Математическая статистика для вузов/ Г.А. Соколов, И.М. Гладких. – 2-е изд., исправл.- М.: Издательство «Экзамен», 2007
б) дополнительная литература
1. Гудыма А.П. Лабораторный практикум по математической статистике: методические указания и варианты индивидуальных заданий для выполнения расчетно-графических работ в 3-х частях, Тюмень 2000 г.
Приложение 1
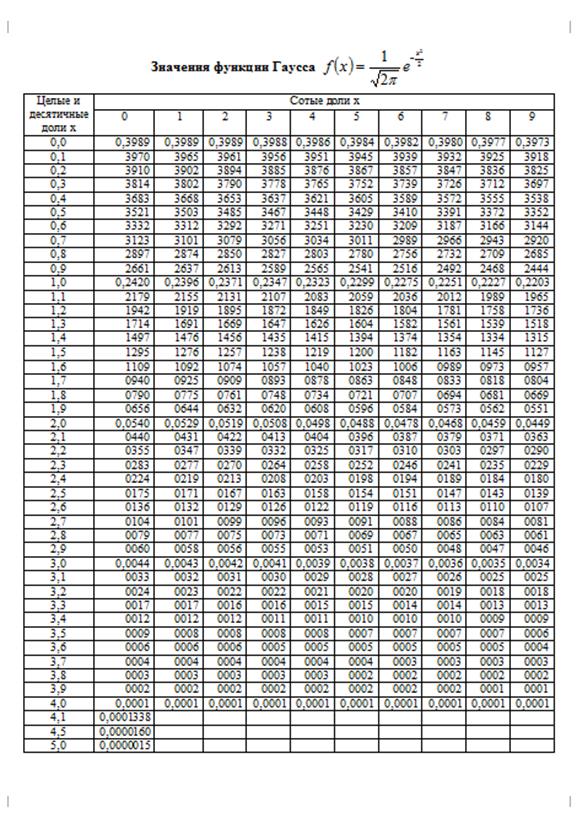
МАТЕМАТИКА
Методические рекомендации по организации и выполнению расчетно-графической работы № 3 для студентов ИДО, направления подготовки 20.03.01 Техносферная безопасность
Тюмень, 2016
УДК
ББК
Составитель: доцент кафедры математики и информатики, к.п.н., М.В. Виноградова
Математика. Методические указания и варианты расчетно-графической работы № 3 для студентов института дистанционного образования направления подготовки 20.03.01 Техносферная безопасность / М.В. Виноградова – Тюмень, 2016 – 93 с. –электронный ресурс
Методические указания разработаны для студентов института дистанционного образования направления подготовки 20.03.01 Техносферная безопасность. Предназначены для выполнения расчетно-графической работы № 3 по дисциплине «Математика».
Рецензент: Н.Н. Мальчукова– к.п.н., доцент кафедры математики и информатики ГАУ Северного Зауралья
УТВЕРЖДЕНО
на заседании кафедры математики и информатики
протокол № 3 от 30 ноября 2016 г.
методической комиссией механико-технологического института
протокол 3 № от 6 декабря 2016 г.
© ГАУ Северного Зауралья, 2016
© М.В. Виноградова, 2016
Оглавление
Введение
Требования к выполнению и оформлению контрольных работ.
РАЗДЕЛ I.
СЛУЧАЙНЫЕ СОБЫТИЯ
Глава 1.
События и вероятность
1.1.
Некоторые формулы комбинаторики
1.2.
Основные понятия теории вероятности
1.3.
Классическое определение вероятности
1.4.
Статистическое определение вероятности
Примеры решения типовых задач 9
Глава 2.
Теоремы сложения вероятностей
2.1.
Сложение вероятностей
2.2.
Умножение вероятностей независимых событий
2.3.
Условная вероятность
Примеры решения типовых задач 12
Глава 3.
Следствие теорем сложения и умножения
3.1.
. Формула полной вероятности
3.2.
Формула Байеса
Примеры решения типовых задач 16
Глава 4.
Повторение испытаний
4.1
Формула Бернулли
4.2.
Локальная и интегральная формулы Муавра- Лапласа
4.3.
Формула Пуассона
Примеры решения типовых задач
Контрольный тест после изучения раздела I «Случайные события»
РАЗДЕЛ II.
СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
Глава 5.
Дискретная случайная величина
5.1.
Основные понятия случайных величин
5.2.
Числовые характеристики дискретной случайной величины
Примеры решения типовых задач 28
Глава 6.
Непрерывная случайная величина
6.1.
Функция и плотность распределения непрерывной случайной величины
6.2.
Числовые характеристики непрерывной случайной величины
Примеры решения типовых задач
Контрольный тест после изучения раздела II «Случайные величины»
РАЗДЕЛ III.
ВЫБОРОЧНЫЙ МЕТОД
Глава 7.
Выборочный метод
Генеральная и выборочная совокупности. Виды выборки
Статистическое распределение выборки
Графическое изображение статистического распределения выборки и эмпирической функции распределения.
Глава 8.
Статистические оценки параметров распределения
Оценки параметров распределения
Понятия генеральной и выборочной средней. Формулы вычисления
Понятия генеральной и выборочной дисперсий и формулы вычисления
Точность оценки, доверительная вероятность (надежность). Доверительный интервал.
РАЗДЕЛ IV.
СТАТИСТИЧЕСКАЯ ПРОВЕРКА СТАТИСТИЧЕСКИХ ГИПОТЕЗ
Глава 9.
Проверка гипотез
9.1.
Понятие статистической гипотезы
9.2.
Критическая область. Область принятия гипотезы. Критические точки
9.3
Проверка гипотезы о нормальном распределении генеральной совокупности. Критерий согласия Пирсона
9.4
Методика вычисления теоретических частот нормального распределения
Пример решения типовой задачи
Контрольный тест после изучения раздела «Статистическая проверка статистических гипотез»
РАЗДЕЛ V
ЭЛЕМЕНТЫ ТЕОРИИ КОРРЕЛЯЦИИ
Глава 10.
Элементы корреляционного анализа
10.1.
Основные понятия корреляционного анализа.
10.2.
Корреляционная таблица и корреляционное поле
10.3
Выборочное уравнение регрессии
10.4.
Выборочный коэффициент корреляции
10.5.
Оценка тесноты любой связи
Пример решения типовой задачи
Контрольный тест после изучения раздела V «Элементы теории корреляции»
Задания для контрольной работы № 3
Контрольные вопросы к итоговой аттестации по предмету
Учебно-методическое и информационное обеспечение дисциплины
Выполнение и оформление контрольных работ
1. Слушатели выполняют контрольную работу в соответствии с учебным планом в сроки, установленные ИДО.
2. Каждая контрольная работа выполняется в отдельной тетради в клеточку, ручкой любого цвета, кроме зеленого и красного, аккуратно и разборчивым почерком, чертежи выполняются простым карандашом с использованием инструмента.
3. На титульном листе следует указать фамилию, имя, отчество слушателя, его адрес с указанием почтового индекса, номер зачетной книжки, номер варианта.
4. Задания в контрольных работах выполняются по порядку, согласно расположению их в варианте.
5. На заключительном листе контрольных работ следует указать список литературы, которым Вы пользовались при их выполнении.
6. Если контрольные работы выполнены с нарушением всех вышеперечисленных указаний или не полностью, то они возвращаются слушателю для доработки без проверки.
7. Если работы не зачтены, внимательно изучите все замечания рецензента. Переделайте работы в соответствии с рекомендациями рецензента.
8. Переделанные работы предоставляются на проверку вместе с незачтенными работами.
9. Слушатель выполняет тот вариант контрольных работ, который совпадает с последней цифрой его учебного шифра.
При этом если предпоследняя цифра учебного шифра – нечетное число (1,3,5,7,9),то номера задач для соответствующего варианта даны в таблице № 1; если же предпоследняя цифра учебного шифра – четное число или ноль (2,4,6,8,0), то номера задач для соответствующего варианта даны в таблице № 2.
Таблица № 1.
| № варианта | ||||||||
Номера заданий для контрольной работы № 4
Таблица № 2.
| № варианта | ||||||||
Дата: 2019-05-28, просмотров: 453.