Задача Коши для ОДУ n-го порядка ставится следующим образом

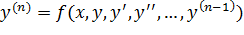
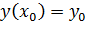
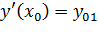                                                                                        (4.18)

………………….

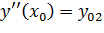
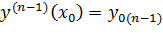
Здесь 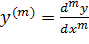 производная m порядка от решения, m=1,2,…,n.

Основной прием, используемый при решении задач, заключается во введении новых переменных и сведению задачи ОДУ высокого порядка к решению системы ОДУ первого порядка.

Введем новые переменные:

……….

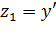
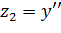
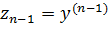
Перепишем задачу в виде систему ОДУ первого порядка:

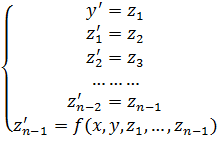
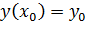
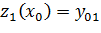
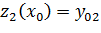
……………..                                                                                  (4.19)

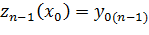
Полученная система, состоящая из n ОДУ первого порядка с соответствующими начальными условиями, решается любым из описанных методов.

Пусть необходимо решить задачу Коши для ОДУ второго порядка:

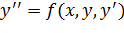
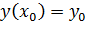
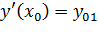                                                                                        (4.20)

Путем введения замены 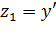, сведем (4.18) к системе:

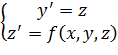
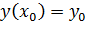
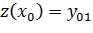                                                                                                  (4.21)

Которую можно решить любым из представленных методов.

Пример :

На интервале [0,1] с шагом h=0.2 решить задачу Коши методом Рунге-Кутты 4 порядка.

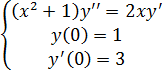
Численное решение сравнить с аналитическим решением: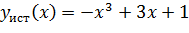

Решение :

Введем новую переменную 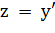. Задача сводится к решению системы двух ДУ первого порядка.

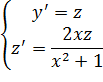
y(0) = 1

z(0) = 3

Данную систему решим методом Рунге-Кутты с использованием формул (4.16)

Вычислим значение вспомогательных величин:

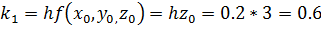
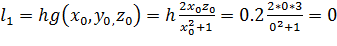
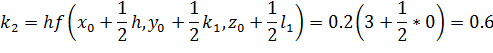
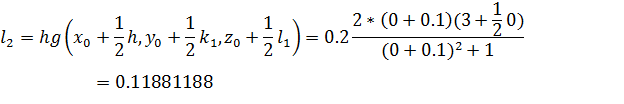
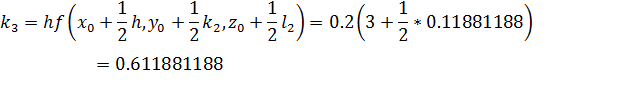
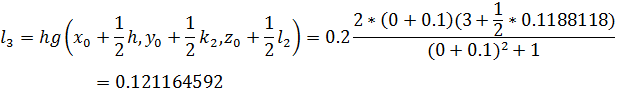
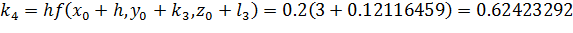
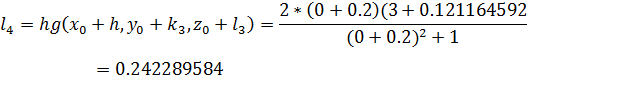
Найдем приращение функции на первом интервале:

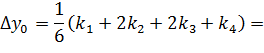
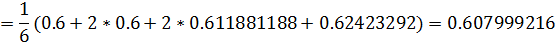
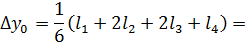
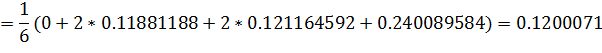
И значения функций в первом узле:

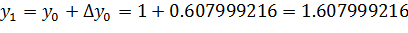
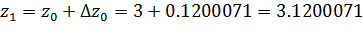
Аналогично получим решения в остальных узлах, результаты вычислений занесем в таблицу.

k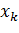
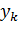
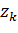
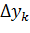
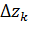
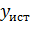
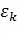
0	0.0	1.0000000	3.00000000	0.607999216	0.1200E+00	1.000000	0.000000
1	0.2	1.607999216	3.120007088	0.655995430	0.3600E+00	1.607999216	0.784E-6
2	0.4	2.263994646	3.480019051	0.751991317	0.6000E+00	2.263994646	0.535E-5
3	0.6	3.015985963	4.080024218	0.895987662	0.8400E+00	3.015985963	0.140E-4
4	0.8	3.911973624	4.920018746	1.087984366	0.1080E+01	3.911973624	0.264E-4
5	1.0	4.999957990	6.000004180			5.000000000	0.420E-4

Решением задачи является табличная функция (оставлены 5 значащих цифр в каждом числе):

k	0	1	2	3	4	5
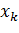
	0.00000	0.20000	0.40000	0.60000	0.80000	1.00000
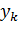
	1.00000	1.60799	2.26399	3.01598	3.91197	4.99996

9.4. Осциллятор Ван дер Поля.

Нелинейное уравнение Ван дер Поля имеет вид:

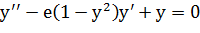                                                         (1)

Уравнение (1) характеризует колебательную систему с переменным коэффициентом демпфирования. При больших отклонениях y (y > 1) демпфирование является положительным и наоборот, при малых отклонениях (y<1) демпфирование становится отрицательным. Следовательно, можно предположить наличие в системе предельного цикла в зависимости от параметра e.

Задание:

Промоделировать систему при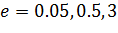

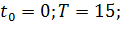
1)

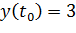
2)

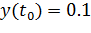
Приведение к нормальной форме Коши:

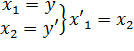
Тогда уравнение (1) примет вид:

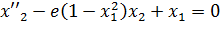
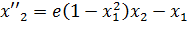
Таким образом (1) сведено к СОДУ в нормальной форме Коши.

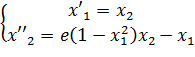
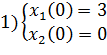
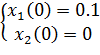
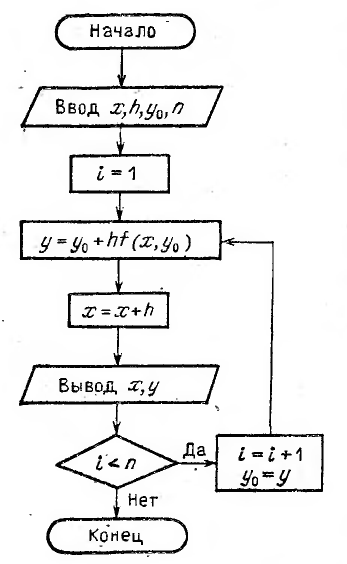
Блок-схема алгоритма решения задачи Коши методом Эйлера изображена на рисунке. Задаются начальные значения x, y, величина шага h и количество точек n.

Список литературы

Основная литература

1. Амосов А.А., Дубинский Ю.Д., Копчёнова Н.В. «Вычислительные методы для инженеров» – М.: Высшая шк., 1994 – 544 с.

2. Рябенький А.С. «Введение в дискретную математику: Учебное пособие для вузов» – М.: Физматлит, 1994 – 336 с.

3. Азаров А.И., Басик В.А. и др. «Сборник задач по методам вычислений: учебное пособие для вузов» - под ред. Монастырского – М.: Физматлит, 1991 – 320 с.

4. Дж. Мэтьюз, К. Финг, «Численные методы. Использование MATLAB» / пер. с англ – М.: Вильямс, 2001 – 720 с.

5. «Начало работы в MATLAB» / пер. с англ Конюшенко В.В. – http://www.exponenta.ru/educat/free/matlab/gs.pdf

Дополнительная литература

6. Бахвалов Н.С. «Численные методы, ч.1» – М.: Наука, 1975 – 631 с.

7. Дж. Фарсайт, М. Малькольм «Машинные методы математических вычислений» – М.: Мир, 1980 – 279 с.