Имеем:
(*)
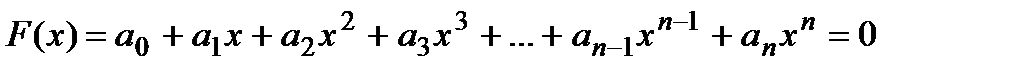
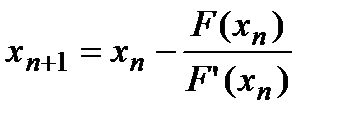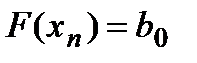, где 
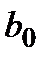вычисляется по правилу Горнера. Но согласно (2):
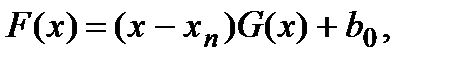
где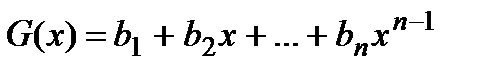 
Поэтому:
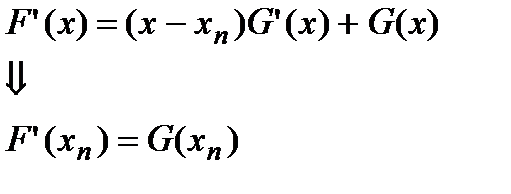
Но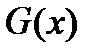 
– это многочлен степени 
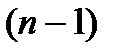. Поэтому, используя правило Горнера, можно вычислить 
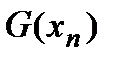. Имеем:
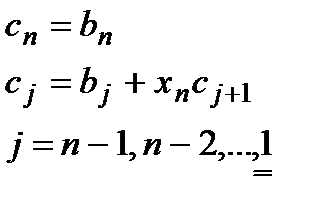
И, соответственно:
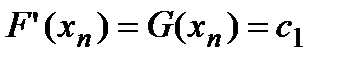
Подставляя найденные значения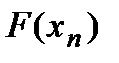 
и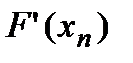 
в (*), получим:
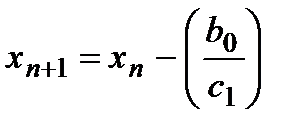
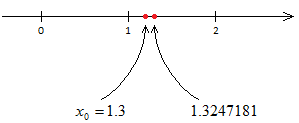
Пример. Найти корень многочлена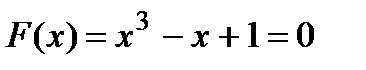 
расположенный вблизи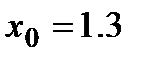 
| 
| 
| 
|
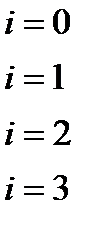
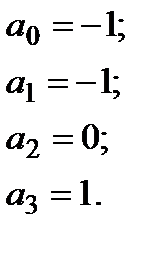
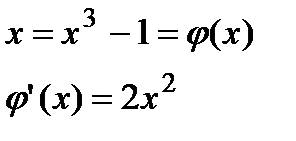
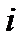
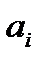
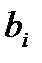
| 3 | 1 |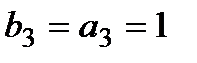 
| 
|
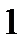
| 2 | 0 |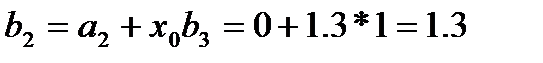 
| 
|
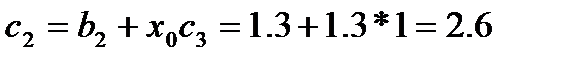
| 1 | -1 |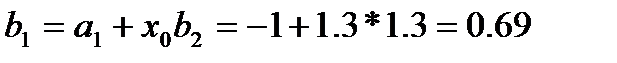 
| 
|
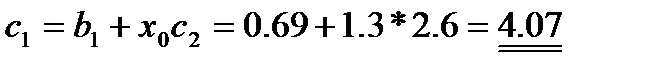
| 0 | -1 |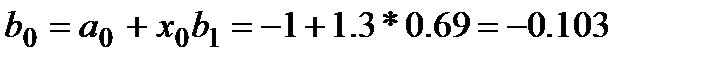 
|
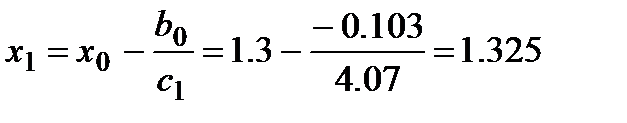
| 3 | 1 | 1 | 1 |
| 2 | 0 | 1.325 | 2.65 |
| 1 | -1 | 0.755625 | 4.267 |
| 0 | -1 | 0.001203 |
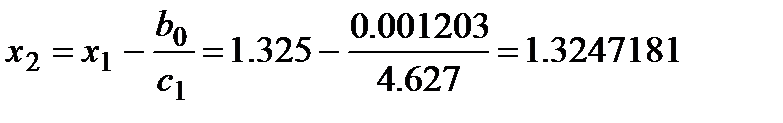
Метод Бирге-Виета
Метод Бирге-Виета представляет из себя улучшенный метод Ньютона-Рафсона с помощью схемы Горнера.
Пусть у нас есть уравнени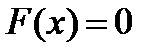е 
, где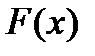 
- полином n порядка, и итерационная формула Ньютона-Рафсона 
.
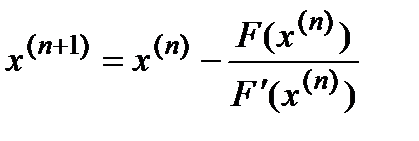По правилу Горнера можно получить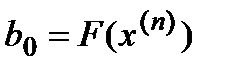 
- смотри формулу (*).
И по формуле (*)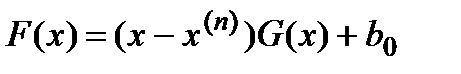 
.
Тогда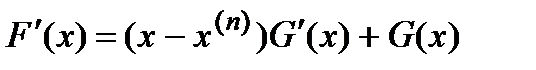 
- отсюда получается, что 
.
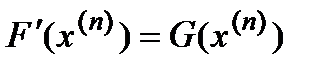Но: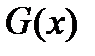 
- многочлен 
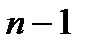степени, поэтому его также можно вычислить по схеме Горнера в следующем виде:
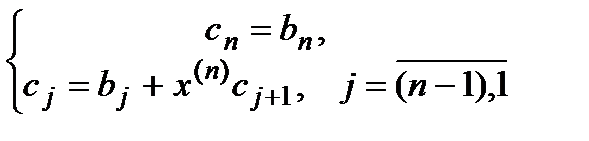
И подставляя найденные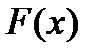 
и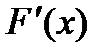 
в формулу Ньютона-Рафсона получаем:
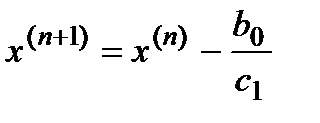
Это и есть основная формула метода Бирге-Виета.
Задача 3.1.
Найти корень полинома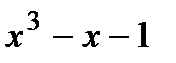 
, расположенный вблизи значения 
.
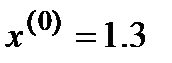Решение методом Ньютона-Рафсона:
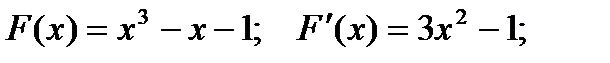
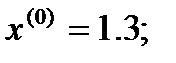
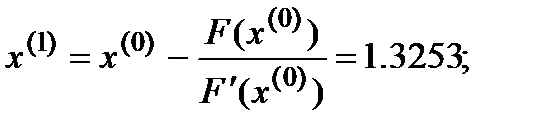
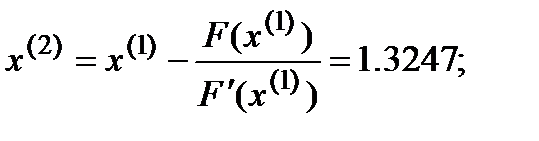
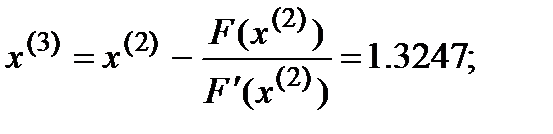
Ответ: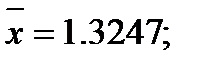 
Решение схемой Горнера:
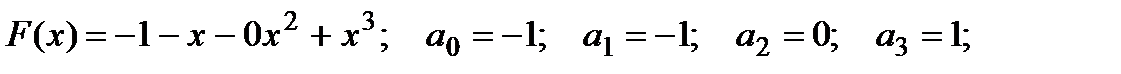
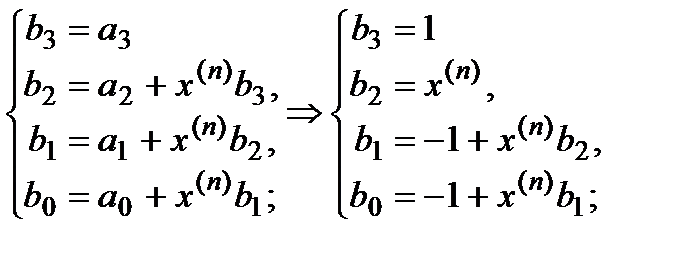- для нахождения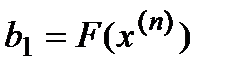 
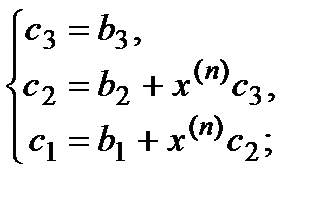- для нахождения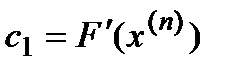 
Первая итерация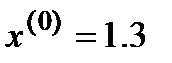 
:
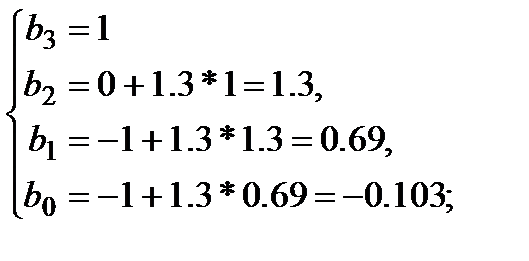
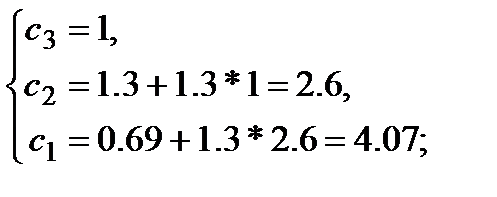
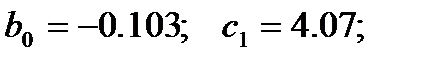
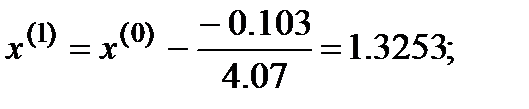
Вторая итерация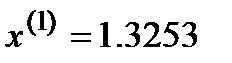 
:
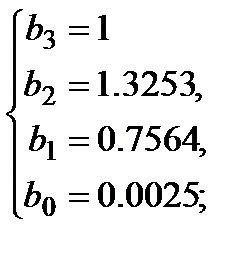
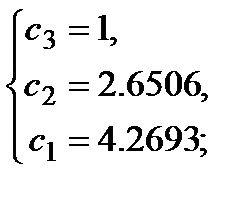
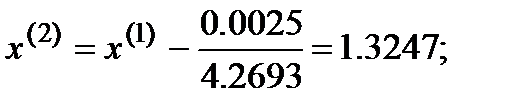
Третья итерация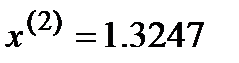 
:
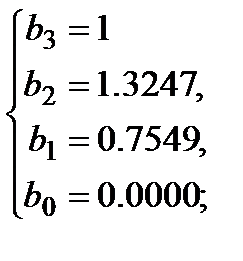
Обратите внимание, что дальше считать не имеет смысла -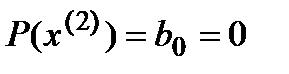 
с точностью до 4 знаков – заданная точность достигнута.
Ответ: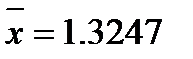 
Решение СЛАУ
СЛАУ – Система Линейных Алгебраических Уравнений – это уравнение вида:
,
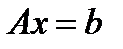где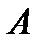 
– матрица размерностью 
, 
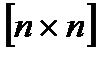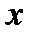и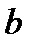 
– вектор-столбцы 
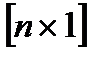, при этом матрица 
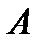не вырожденная (её определитель не равен нулю).
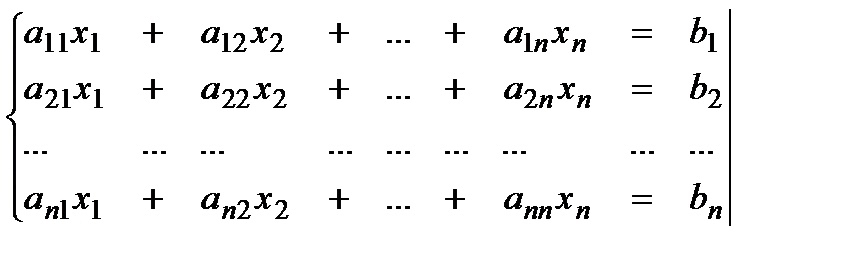(1)
Методы решения СЛАУ бывают прямые и итерационные.
Метод Гаусса
Метод Гаусса – это прямой метод решения СЛАУ. Это метод последовательного исключения неизвестных. Относится к простым методам, т.е. позволяет получить решение СЛАУ за конечное число шагов. Если все операции выполняются точно (без ошибок округления), то решение СЛАУ также получается точным. Метод Гаусса (как и другие простые методы: Крамера, метод ортогонализации и другие) применяется на практике для решения СЛАУ на ЭВМ, как правило, с числами порядка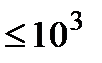 
.
Если матрица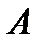 
не вырождена, то существует система вида 
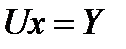, где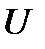 
представляет собой верхнюю треугольную матрицу.
Верхняя треугольная матрица – это матрица, в которой все элементы ниже главной диагонали равны нулю.
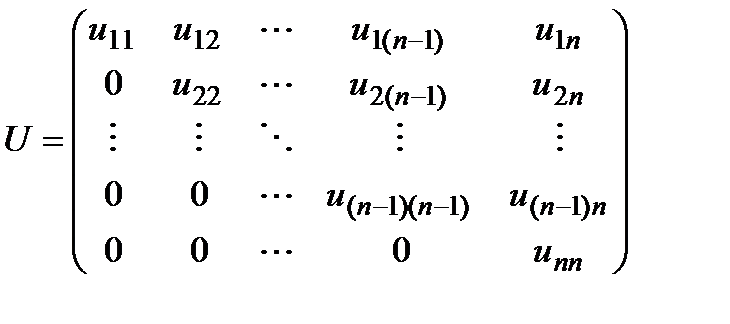
Соответственно, после построения матрицы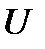 
можно выполнить обратную подстановку снизу вверх и получить решение исходной СЛАУ. Обратите внимание, что и построение верхней треугольной матрицы, и обратная подстановка выполняются за конечное число шагов.
Расширенная матрица системы – это матрица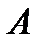 
, к которой справа присоединён столбец 
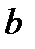. Будем обозначать её как 
:
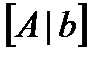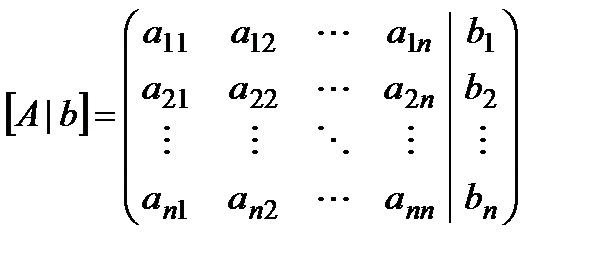
Существуют три элементарные операции над расширенной матрицей, которые приведут к решению эквивалентной СЛАУ:
1. Перестановка – любые две строки можно поменять местами;
2. Масштабирование – любую строку можно умножить на константу, не равную нулю;
3. Замещение – любую строку можно заменить суммой этой же строки и любой другой строки, умноженную на константу, не равную нулю.
Соответственно идея метода Гаусса заключается в построении верхней треугольной матрицы с помощью элементарного ряда операций.
Алгоритм метода Гаусса.
Запишем расширенную матрицу
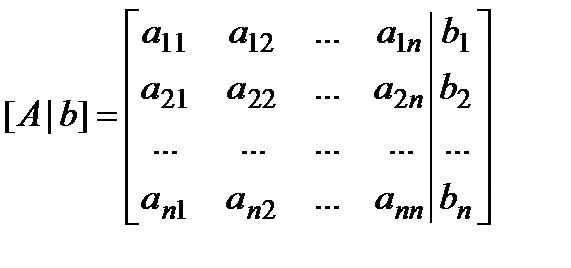(2)
ШАГ 1.
Полагаем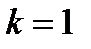 
.
ШАГ 2.
Находим максимальный по модулю элемент среди элементов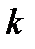 
-го столбца, расположенных не выше главной диагонали:
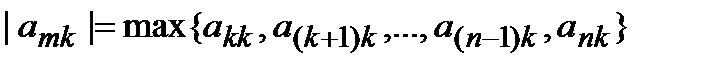(3)
После этого меняем местами строк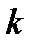и 
и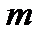 
. Таким образом мы осуществим выбор главного (диагонального) элемента.
Обозначим полученную расширенную матрицу
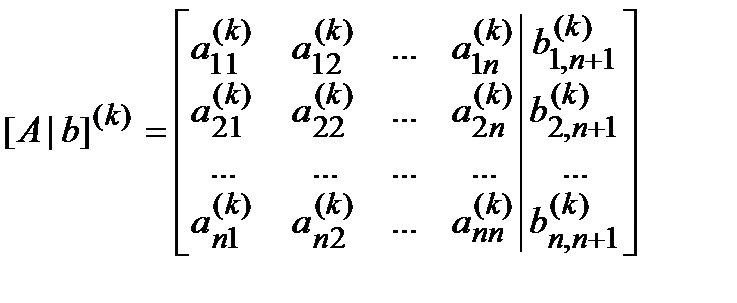(4)
ШАГ 3.
Полагаем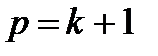 
.
ШАГ 4.
Вычисляем коэффициент
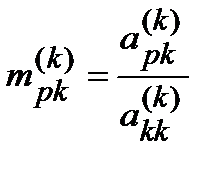(5)
ШАГ 5.
Положим
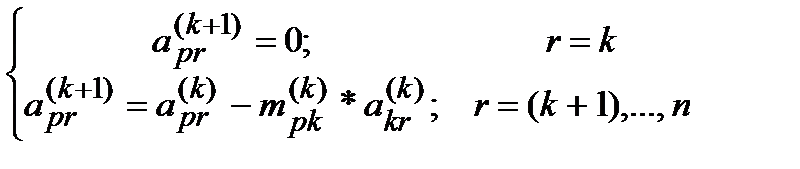(6)
ШАГ 6.
Полагаем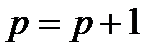 
. Если 
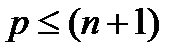, то переходим к шагу 4, иначе переходим к шагу 7.
ШАГ 7.
Полагаем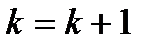 
. Если 
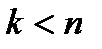, то переходим к шагу 2, иначе переходим к шагу 8.
ШАГ 8.
Процесс построения верхней треугольной матрицы окончен, и она имеет вид:
(7)
ШАГ 9.
Начинаем процесс обратной подстановки:
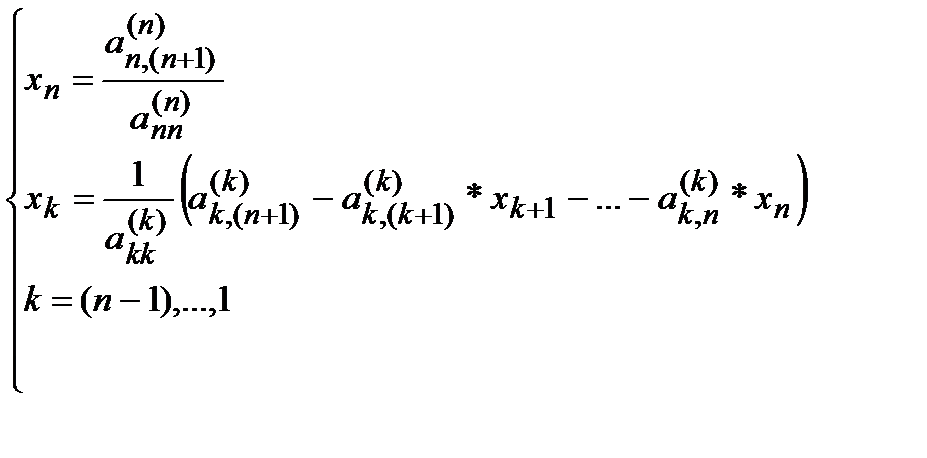(8)
ШАГ 10.
Stop.
Замечание. Существует стратегия тривиального выбора главного элемента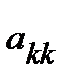 
: если 
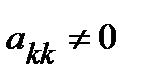, то строки не переставляются, и 
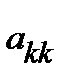– главный элемент. Если 
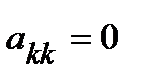, то ищем первую строку ниже 
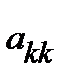, где элемент 
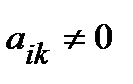и меняем эти строки местами.
Пример 1. Решить СЛАУ:
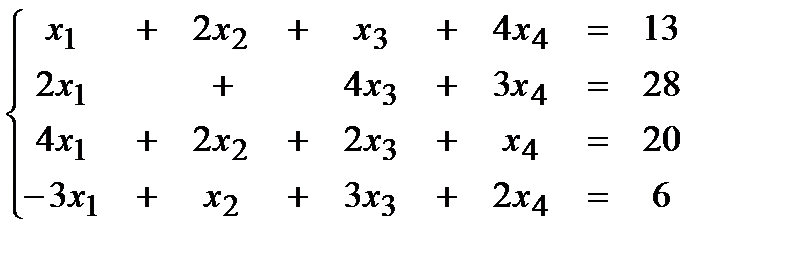
Применим для простоты стратегию тривиального выбора.
Расширенная матрица:
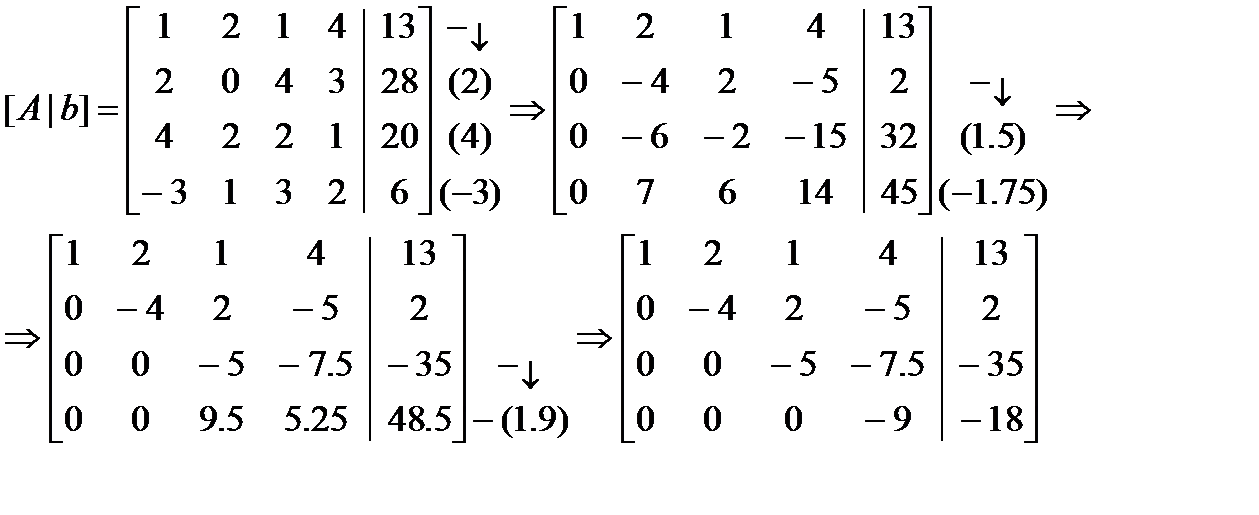
Обратный ход:
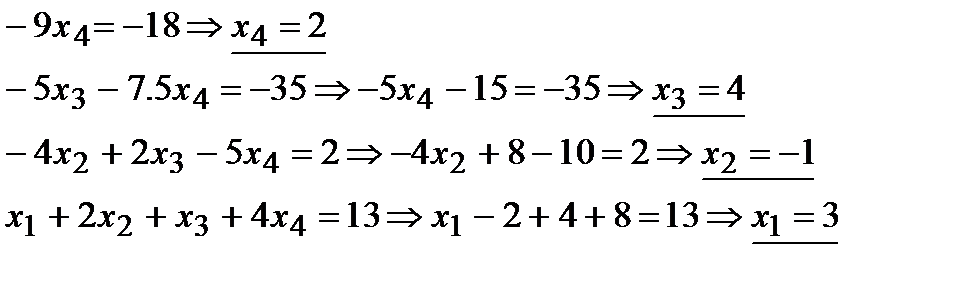
Пример 2. Иллюстрирует, как использование стратегии тривиального выбора главного элемента в методе исключения Гаусса может привести к значительной ошибке в решении СЛАУ.
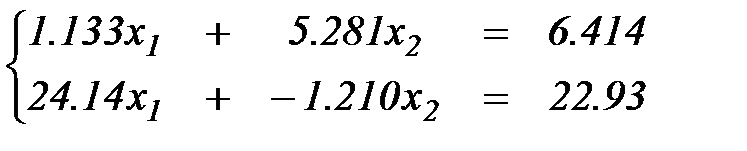
Существует точное решение СЛАУ: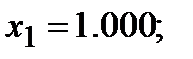 
I. Будем использовать арифметику с четырьмя знаками точности, плюс стратегию тривиального выбора.
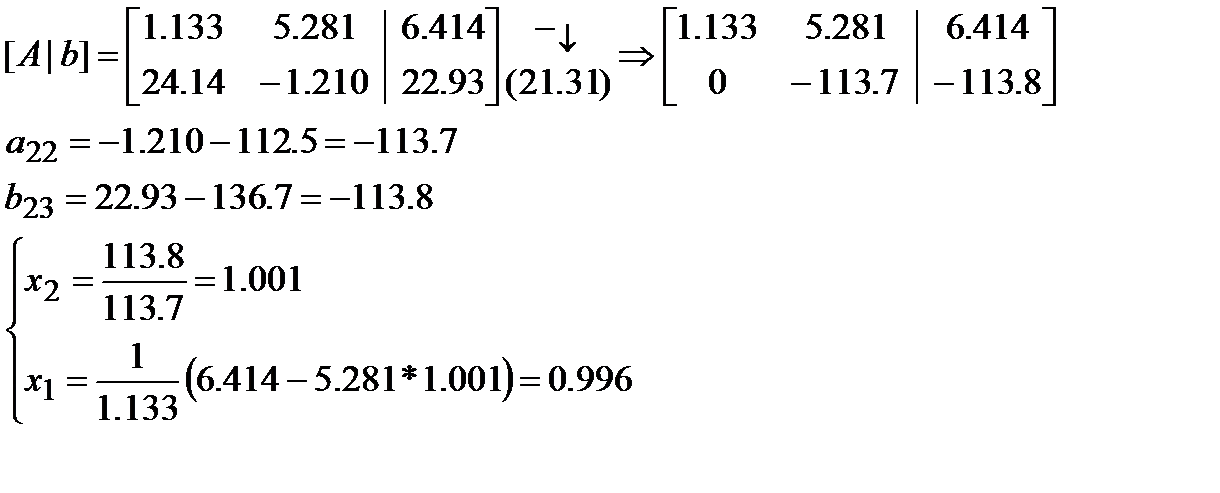
Ошибка обусловлена большим коэффициентом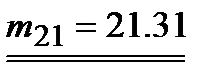 
.
II. Применим стратегию выбора наибольшего главного элемента.
Т.к.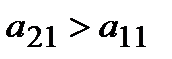 
, меняем местами строки. Получаем:
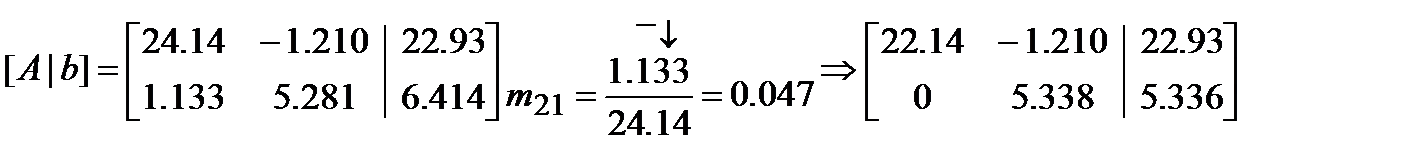
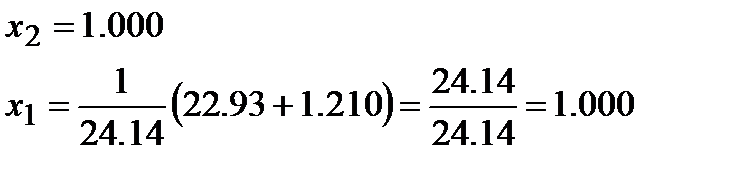
Замечание: Известно, что чем меньше коэффициенты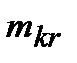 
, тем меньше относительная ошибка при выполнении операций +, –, *, /, 
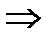тем точнее СЛАУ.
Дата: 2019-05-28, просмотров: 330.
