Рассматривается задача Коши для одного дифференциального уравнения первого порядка разрешенного относительно производной:

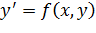
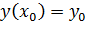
Пусть дано дифференциальное уравнение первого порядка .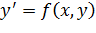

Требуется найти функцию 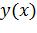, удовлетворяющую при  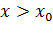дифференциальному уравнению и при 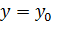начальному условию:

.

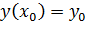Теорема существования и единственности задачи Коши:

Пусть функция 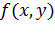определена и непрерывна на множестве точек .

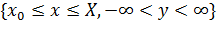Предположим также, что она удовлетворяет условию Липшица: 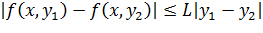для всех 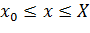и произвольных 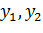, где L - некоторая константа (постоянная Липшица).

Тогда для каждого начального значения 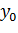существует единственное решение 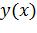задачи Коши, определенное на отрезке .

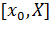Геометрически задача интегрирования дифференциальных уравнений состоит в нахождении интегральных кривых, которые в каждой своей точке имеют заданное направление касательной. Заданием начального условия мы выделяем из семейства решений ту единственную кривую, которая проходит через фиксированную точку .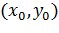

Метод Эйлера.

Метод Эйлера играет важную роль в теории численных методов решения ОДУ, хотя и не часто используется в практических расчетах из-за невысокой точности.

Численное решение задачи Коши состоит в построении таблицы приближенных значений 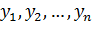в точках .
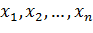Точки 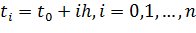называются узлами сетки, а величина h - шагом сетки.

В основе построения дискретной задачи Коши лежит тот или иной способ замены дифференциального уравнения его дискретным аналогом. Простейший метод основан на замене левой части уравнения правой разностной производной: 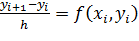. Разрешая уравнение относительно 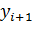, получаем расчетную формулу метода Эйлера: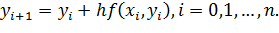

Локальной погрешностью метода называется величина .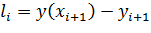

Найдем величину локальной погрешности метода Эйлера:                 ,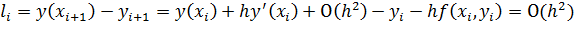

при условии, что .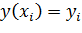

Другими словами 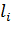- погрешность, которую допускает за один шаг метод, стартующий с точного решения. Глобальной погрешностью (или просто погрешностью) численного метода называют сеточную функцию 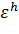со значениями 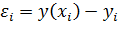в узлах.

В качестве меры абсолютной погрешности метода примем величину .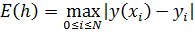

Можно показать, что для явных одношаговых методов из того, что локальная погрешность имеет вид 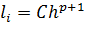следует, что 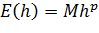, где C и M - некоторые константы.

Таким образом, метод Эйлера является методом первого порядка точности. Для нахождения решения задачи Коши с заданной точностью 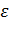требуется найти такое приближенное решение 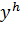, для которого величина глобальной погрешности .

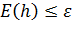Так как точное решение задачи неизвестно, погрешность оценивают с помощью правила Рунге.

Правило Рунге оценки погрешностей. Для практической оценки погрешности проводят вычисления с шагами 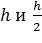. За оценку погрешности решения, полученного с шагом 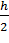, принимают величину, равную 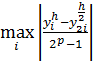, где p - порядок метода.