Пусть 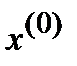 – приближенное решение СЛАУ (1). Подставим
– приближенное решение СЛАУ (1). Подставим 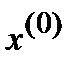 в (1):
в (1):
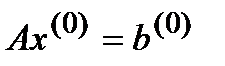 (9)
(9)
Если компоненты 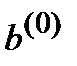 существенно отличаются от
существенно отличаются от 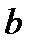 , то
, то 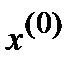 – не является достаточно хорошим приближением к решению СЛАУ (1). С другой стороны, даже если
– не является достаточно хорошим приближением к решению СЛАУ (1). С другой стороны, даже если 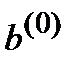 и
и 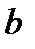 близки, то
близки, то 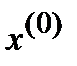 всё равно может быть плохим приближением к решению СЛАУ.
всё равно может быть плохим приближением к решению СЛАУ.
Вычтем каждое уравнение (9) из каждого уравнения (1) и обозначим:
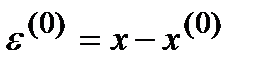 (10)
(10)
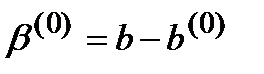 (11)
(11)
Тогда можно записать:
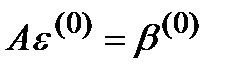 (12)
(12)
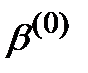 легко вычисляется, после чего СЛАУ (12) может быть решена относительно
легко вычисляется, после чего СЛАУ (12) может быть решена относительно 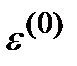 методом исключения Гаусса.
методом исключения Гаусса.
Новое приближение к решению СЛАУ (1):
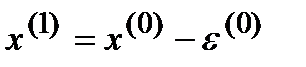 (13)
(13)
Далее, 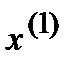 снова можно подставить в (1):
снова можно подставить в (1):
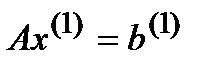 (14)
(14)
Вычтем каждое уравнение (14) из (1) и обозначим
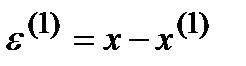
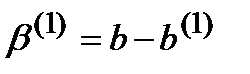
Получим СЛАУ:
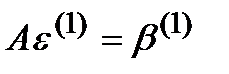
которая также решается методом исключения Гаусса.
И так далее. Процесс можно повторять до тех пор, пока все 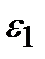 не станут достаточно малыми.
не станут достаточно малыми.
Пример. Рассмотрим СЛАУ:
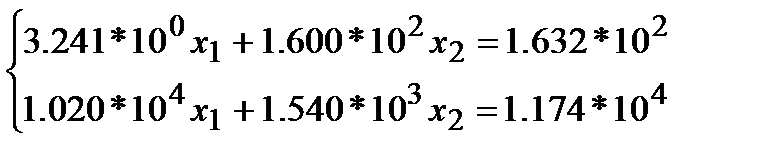 (1*)
(1*)
Точное решение данной СЛАУ:
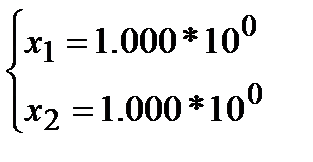
Решим эту СЛАУ методом исключения Гаусса со стратегией тривиального выбора главного элемента и арифметикой с четырьмя знаками точности:
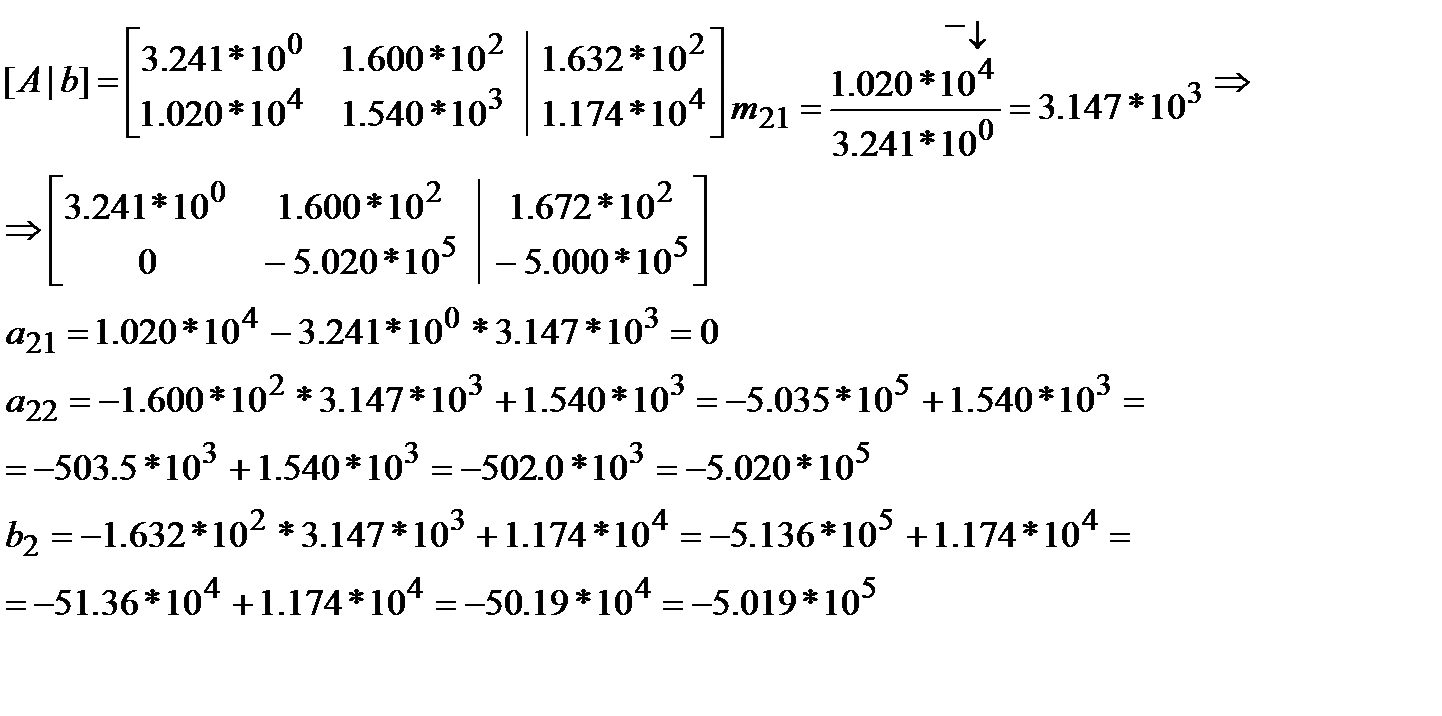
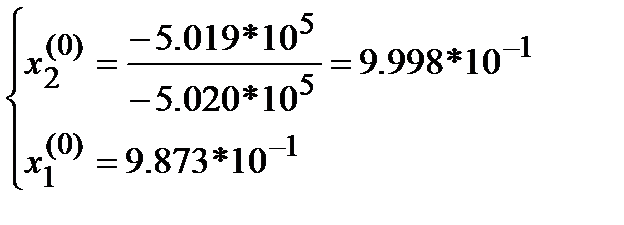 (2*)
(2*)
Подставим (2*) в (1*). Получим:
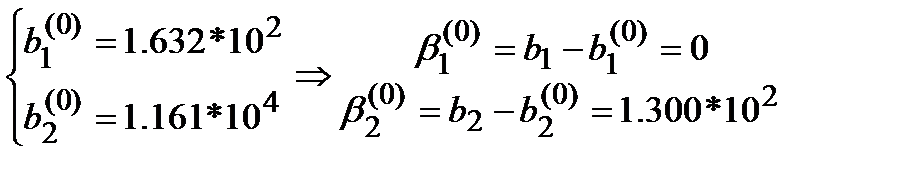
Решим СЛАУ:
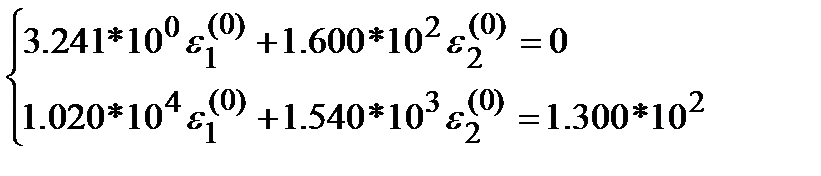 (3*)
(3*)
Применяя метод Гаусса без перестановок уравнений получим:
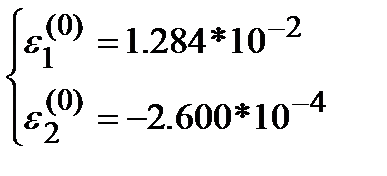
Поэтому новое приближение:
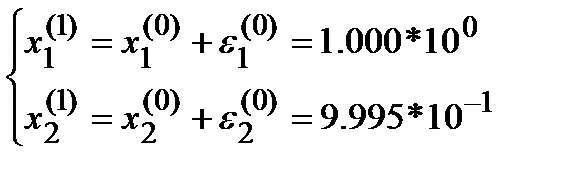
Подставим эти значения в (1*) и получим:
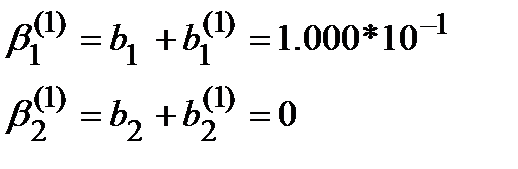
Решаем СЛАУ и получаем:
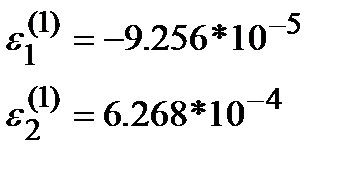
Далее:
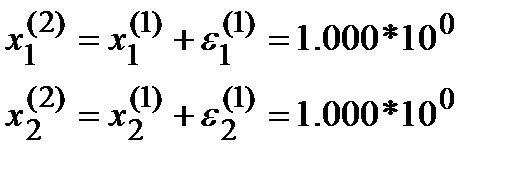 (4*)
(4*)
Таким образом удалось получить точное решение (4*) СЛАУ (1*) с помощью трёх итераций.
Замечание: Если бы сразу выбрали стратегию максимального главного элемента, то точное решение было бы получено за одну итерацию.
Пример 2. Решить систему уравнений методом Гаусса на шестиразрядной десятичной ЭВМ.
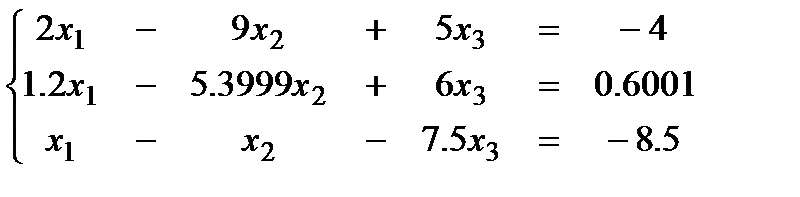 (*)
(*)
Примечание: Точное решение СЛАУ:
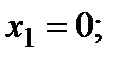
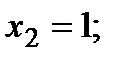
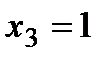
После решения методом Гаусса получаем:
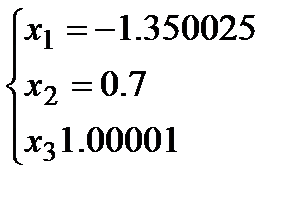 – плохо!
– плохо!
Причина: использование на втором шаге малого ведущего элемента 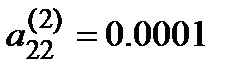 . Следовательно появился большой множитель
. Следовательно появился большой множитель 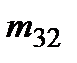 и имеет место существенное вырастание коэффициента в последнем уравнении.
и имеет место существенное вырастание коэффициента в последнем уравнении.
Решение.
Прямой ход.
Шаг 1. 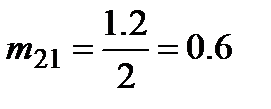 ;
; 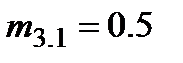
Расширенная матрица преобразуется к виду:
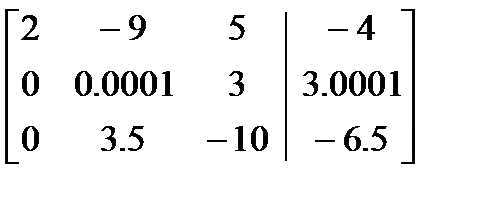
Шаг 2. 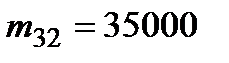
Расширенная матрица преобразуется к виду:
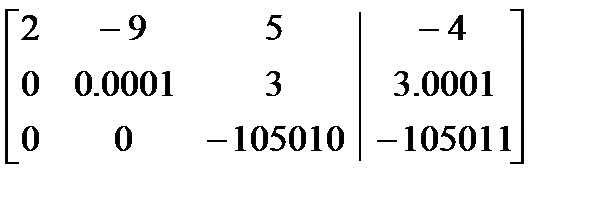
Действительно,
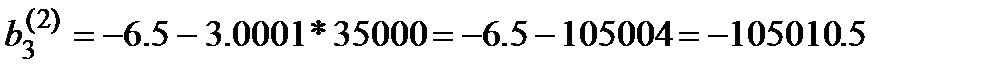
Однако, для шестиразрядной сетки будет получено 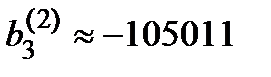 .
.
Обратный ход.
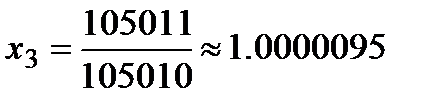
Для шестиразрядной сетки получим 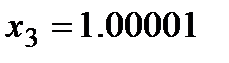
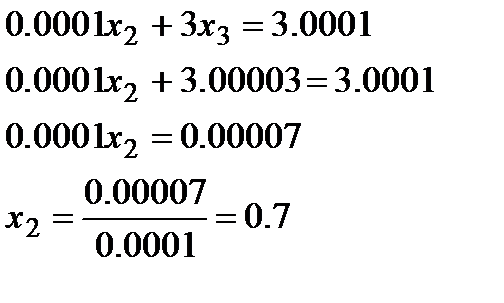
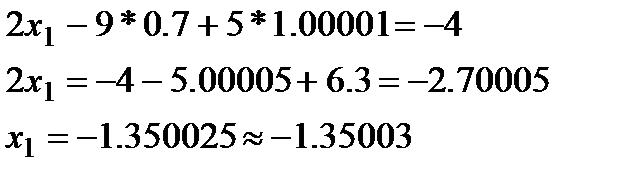
Таким образом:
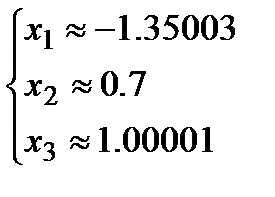 – плохо!
– плохо!
Пример 2*.
Решить систему (*) методом Гаусса с выбором главного элемента по столбцу на шестиразрядной десятичной ЭВМ.
Получаем:
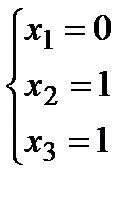 – решение получилось точным.
– решение получилось точным.
Решение.
Прямой ход.
Шаг 1. В первом столбце максимальный элемент находится на диагонали, поэтому перестановка уравнений не требуется, и шаг 1 осуществляется так же, как и в предыдущем примере.
Шаг 2. Во втором столбце
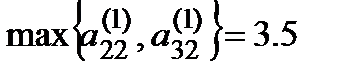 ,
,
поэтому необходимо поменять местами второе и третье уравнения. Получаем:
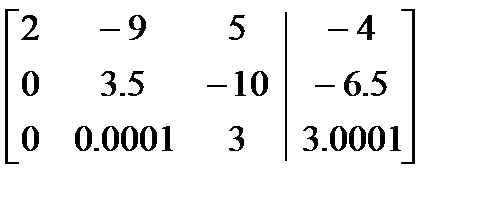
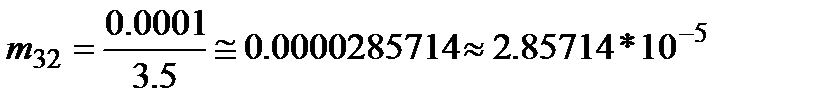
Тогда
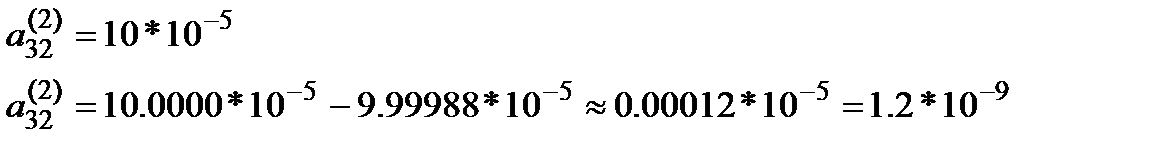
Метод Гаусса-Зейделя
Метод Гаусса-Зейделя является итерационным методом.
Рассмотрим самое обычное СЛАУ:
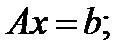 (1)
(1)
Выполним следующие преобразования.
Умножим обе части уравнения на транспонированную матрицу 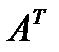 слева (напомним, что умножение матриц некоммутативно!):
слева (напомним, что умножение матриц некоммутативно!):
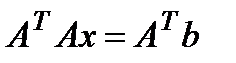 (2)
(2)
Введём следующие обозначения:
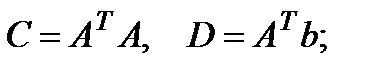
После этого будем заниматься решением следующей СЛАУ, которая эквивалентна исходной:
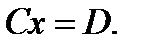 (3)
(3)
Такая СЛАУ называется нормальной, так как матрица C в данном случае будет симметрична относительно главной диагонали. Это свойство нормальности позволяет привести СЛАУ к следующему виду:
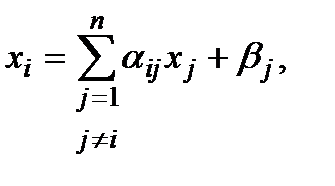 (4)
(4)
где 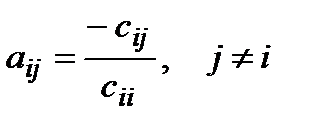 (5)
(5)
и 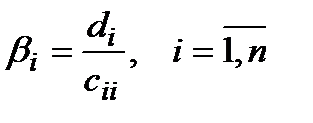 (6)
(6)
Вот эти соотношения и являются теоретической базой метода Гаусса-Зейделя. Теперь организуем итерационный процесс на основе этих соотношений.
Обозначим 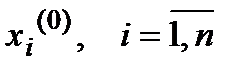 начальное приближение для решения СЛАУ вида
начальное приближение для решения СЛАУ вида 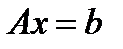 .
.
Вычислим новое приближение по следующим формулам в соответствии с вышеописанной теоретической базой:
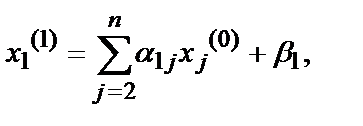 (7.1)
(7.1)
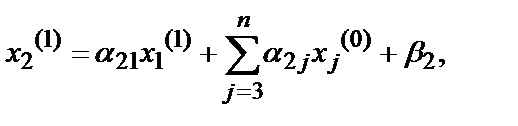 (7.2)
(7.2)
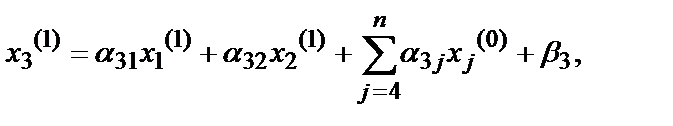 (7.3)
(7.3)
Обратите внимание, что в формировании первого соотношения участвует только первое уравнение, в формировании второго – два первых уравнения и так далее. Поэтому этот метод является достаточно экономичным. Соотношение в общем виде выглядит так:
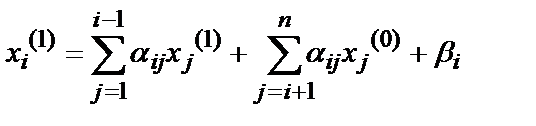 (7.i)
(7.i)
А последнее вычисление имеет вид:
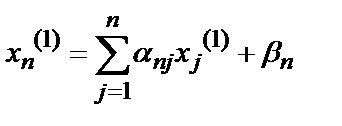 (7.n)
(7.n)
После реализации этих n соотношений у нас оказывается вычисленным очередное приближение 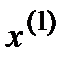 . Чтобы вычислить следующее приближение
. Чтобы вычислить следующее приближение 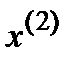 , нужно повторить вычисления.
, нужно повторить вычисления.
Существуют два критерия останова итерационного процесса метода Гаусса-Зейделя – максимальное количество итераций и заданная точность 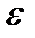 .
.
Справедливо также то, что итерационный процесс Гаусса-Зейделя для приведённой СЛАУ, эквивалентной нормальной, всегда сходится к единственному решению этой системы при любом выборе 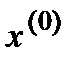 .
.
Теперь в полной мере запишем алгоритм:
ШАГ 1.
Задать 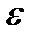 – точность вычислений.
– точность вычислений.
ШАГ 2.
Вычислить 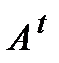 ;
; 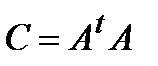 ;
; 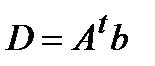 нормальной системы (3).
нормальной системы (3).
ШАГ 3.
Приведение (3) к виду (4)-(6).
ШАГ 4.
Осуществления итерационного процесса по формулам (7).
ШАГ 5.
Вычисление
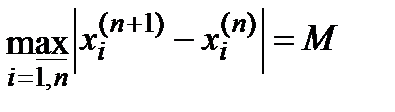
ШАГ 6.
Если 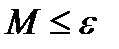 ,
,
то 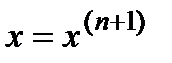 , Stop
, Stop
иначе переход к шагу 4.
Задача 4.2.
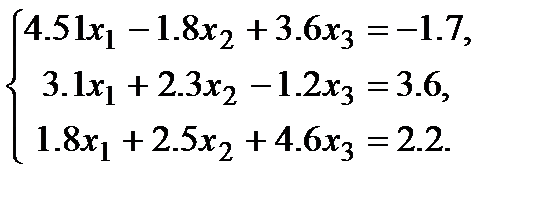
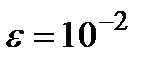
Решение.
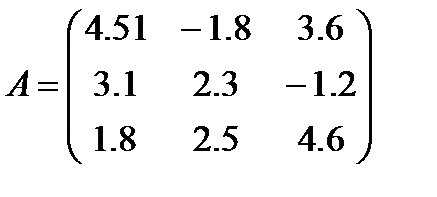
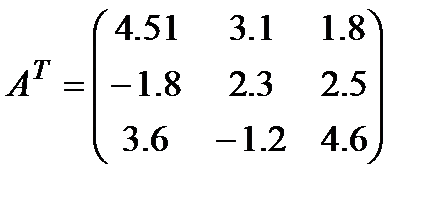
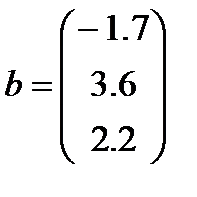

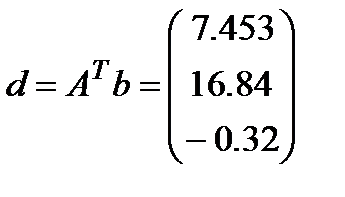
Теперь приведём СЛАУ к нормальному виду:
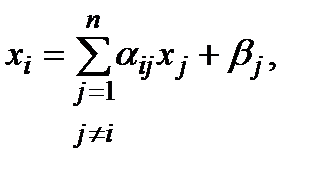
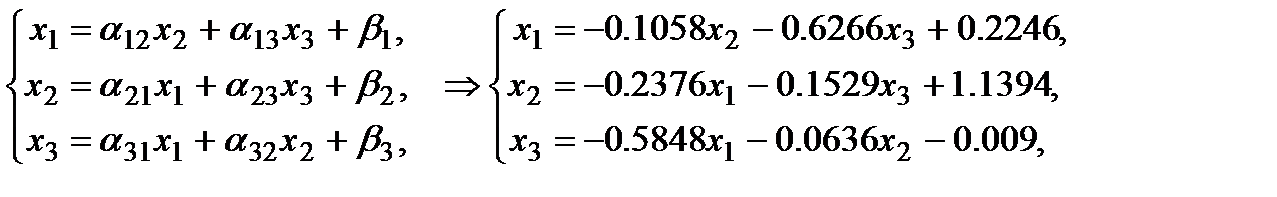
Расставляем индексы:
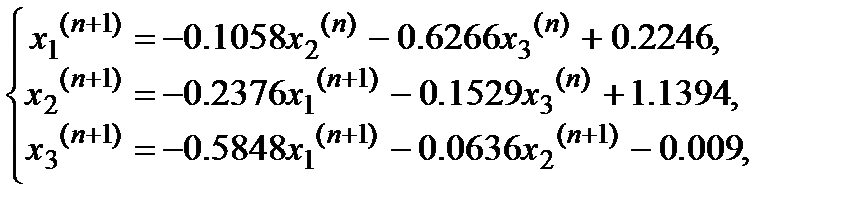
Возьмём начальное приближение 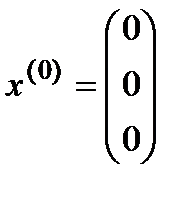 :
:
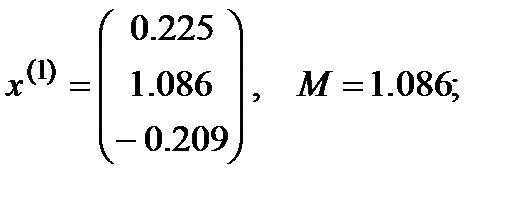
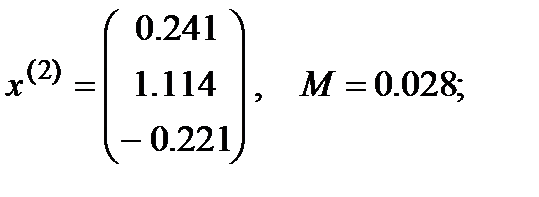
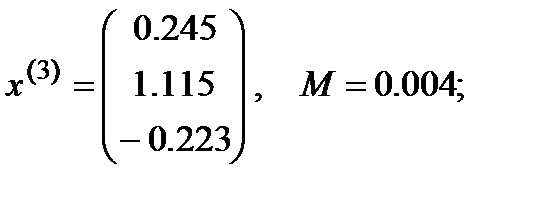
Ответ: 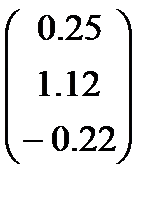
Нормы векторов и матриц
Рассмотрим СЛАУ в матричном виде
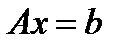 (1)
(1)
где 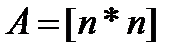 ;
; 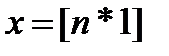 ;
; 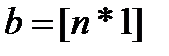 .
.
Пусть 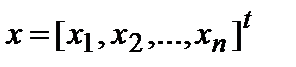 – точное решение (1),
– точное решение (1),
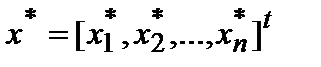 – приблизительное решение (1):
– приблизительное решение (1): 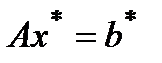 .
.
Погрешность: 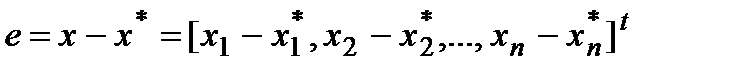 .
.
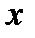 ,
, 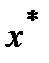 ,
, 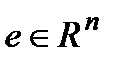 , т.е. являются элементами векторного пространства.
, т.е. являются элементами векторного пространства.
Для оценки величин векторов 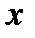 ,
, 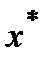 ,
, 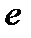 используется понятие нормы вектора.
используется понятие нормы вектора.
Норма вектора
Говорят, что в пространстве 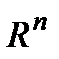 задана норма, если каждому
задана норма, если каждому 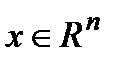 сопоставлено число
сопоставлено число 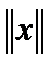 (читается – «норма икс»), обладающее свойствами:
(читается – «норма икс»), обладающее свойствами:
1. 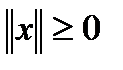 всегда,
всегда,
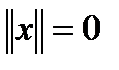 тогда и только тогда, когда
тогда и только тогда, когда 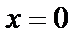
2. 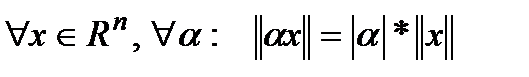
3. 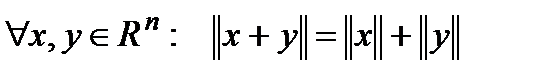
Наиболее распространена норма следующего вида:
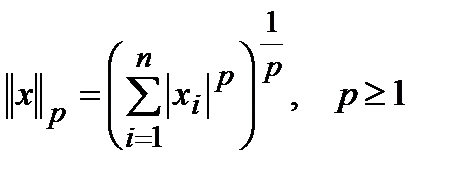 (2)
(2)
Но на практике чаще всего используются следующие частные случаи:
1. 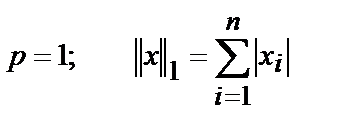 (3)
(3)
2. 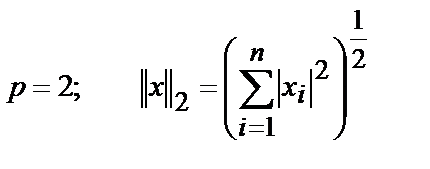 (4)
(4)
3. 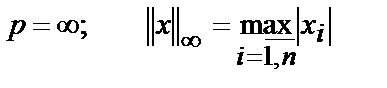 (5)
(5)
Примечания:
1. Норма 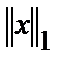 - обычная евклидова норма.
- обычная евклидова норма.
2. Формула для 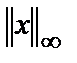 получена из формулы для
получена из формулы для 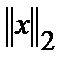 с помощью предельного перехода при
с помощью предельного перехода при 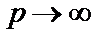 .
.
3. Верно следующее неравенство:
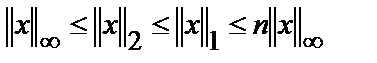
Доказательство:
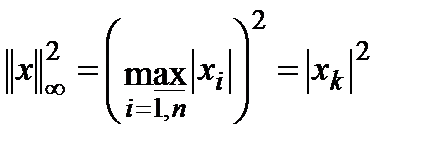 ,
, 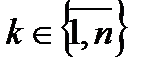
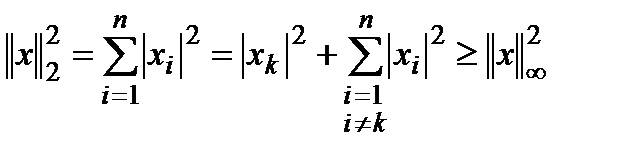
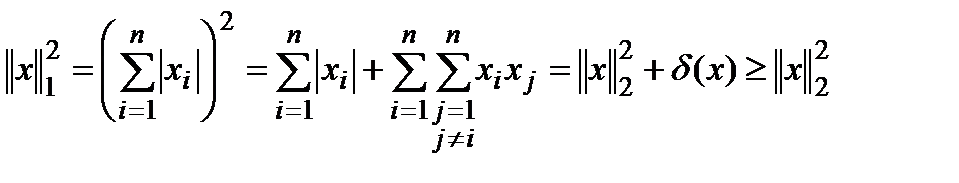
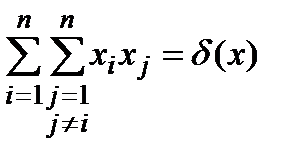
В то же время:
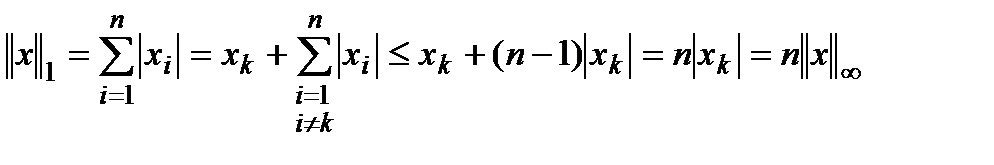
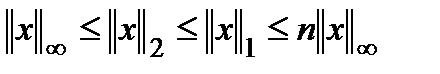
|
Приведём пример. Дан вектор 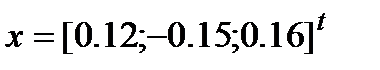 .
.
Найти: 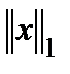 ,
, 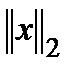 ,
, 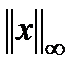 .
.
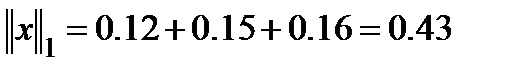
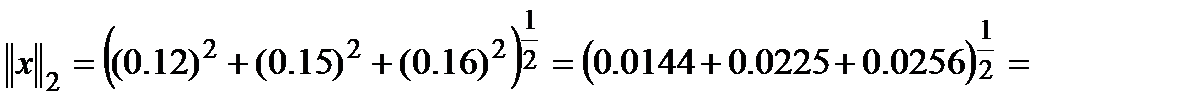
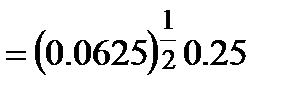
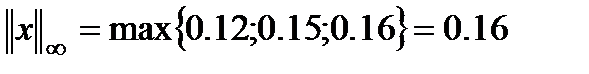
Проверим отношения норм:
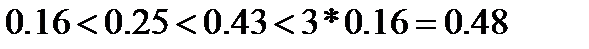
Задача 6.1.
Дан вектор в трёхмерном пространстве 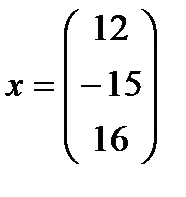 .
.
Найти его нормы 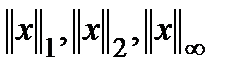 .
.
Решение.
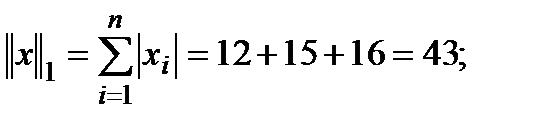
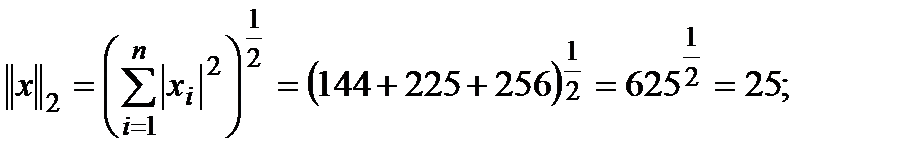
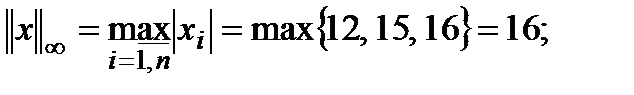
Дата: 2019-05-28, просмотров: 407.