Теорема (без доказательства). Пусть дана функция 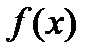 , определённая на отрезке
, определённая на отрезке 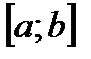 , а также дифференцируемая
, а также дифференцируемая 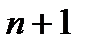 раз на этом отрезке, содержащая узлы интерполяции
раз на этом отрезке, содержащая узлы интерполяции 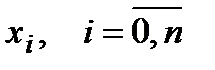 .
.
Тогда для оценки погрешности интерполяции в точке 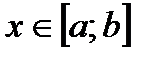 справедливо равенство
справедливо равенство
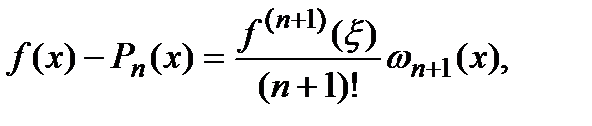
где 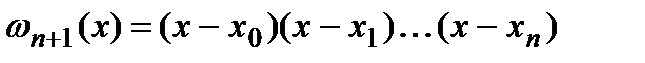 , точка
, точка 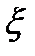 - некоторая точка, находящаяся на отрезке
- некоторая точка, находящаяся на отрезке 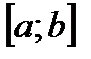 .
.
Основной недостаток этой теоремы в том, что 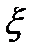 - величина неизвестная. Поэтому при оценке погрешности на практике используется не сама теорема, а следствие из неё.
- величина неизвестная. Поэтому при оценке погрешности на практике используется не сама теорема, а следствие из неё.
Следствие. В условиях этой теоремы допустима также и такая оценка погрешности для 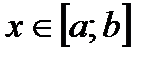 :
:
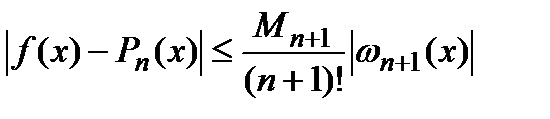 ,
,
а также оценка максимума модуля интерполяции, имеющей вид:
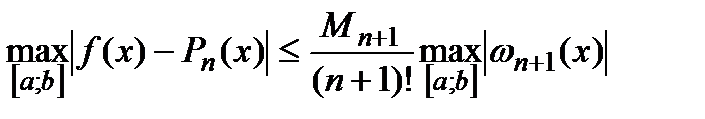 ,
,
где 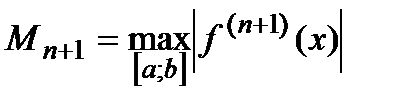 .
.
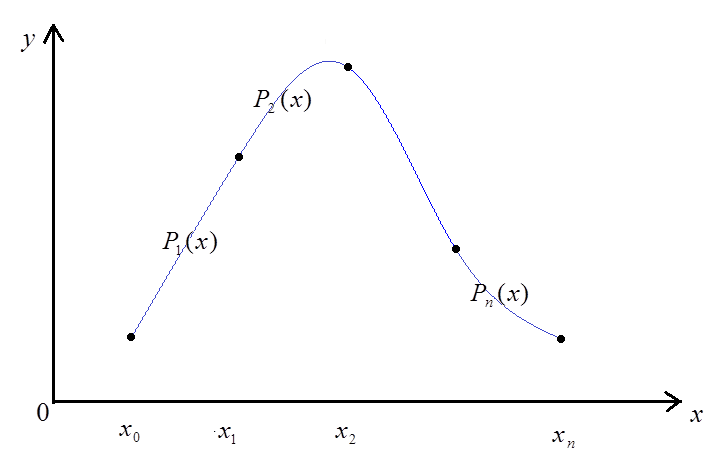
Интерполяция сплайнами
Интерполяция сплайнами придумана для того, чтобы избежать главный недостаток кусочно-полиномиальной интерполяции и построить гладкую функцию. Такая интерполяция сочетает в себе глобальную гладкость и локальную простоту функции по сравнению с другими интерполяциями.
Пусть 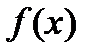 задана таблицей:
задана таблицей:
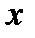
| 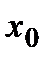
| 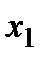
| 
| 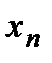
|
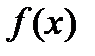
| 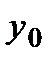
| 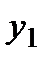
| 
| 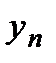
|
Назовём функцию 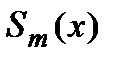 интерполяционным сплайном порядка n для функции
интерполяционным сплайном порядка n для функции 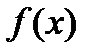 на отрезке
на отрезке 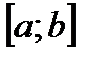 , если выполнены следующие условия:
, если выполнены следующие условия:
1. На всём отрезке 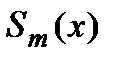 имеет непрерывные производные до порядка
имеет непрерывные производные до порядка  включительно.
включительно.
2. На каждом из частичных отрезков 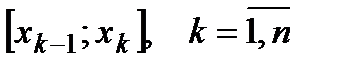
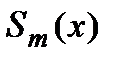 является многочленом степени
является многочленом степени 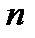 .
.
3. 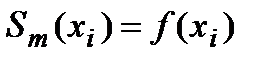 для
для 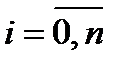 .
.
Дефект сплайна – это разность 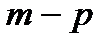 .
.
Самый распространённый вид сплайна – это кубический сплайн с дефектом 1. Рассмотрим его.
По определению сплайн 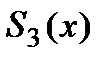 на любом
на любом 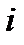 отрезке
отрезке 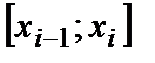 является многочленом
является многочленом 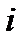 порядка -
порядка - 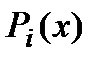 :
:
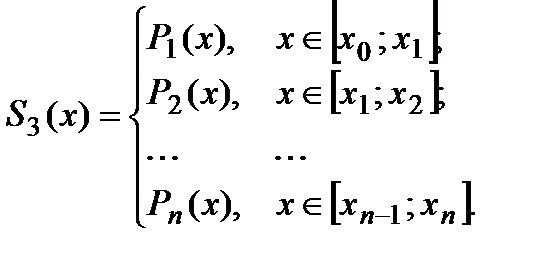
Раз это – кубический многочлен, то мы будем искать 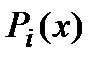 по следующей формуле:
по следующей формуле:
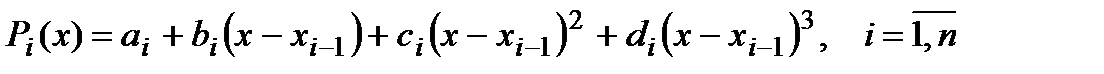 ,
,
где коэффициенты неизвестны и именно их и надо найти – всего 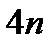 неизвестных.
неизвестных.
По определению сплайна должны выполняться условия совпадения 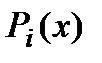 в узлах интерполяции:
в узлах интерполяции:
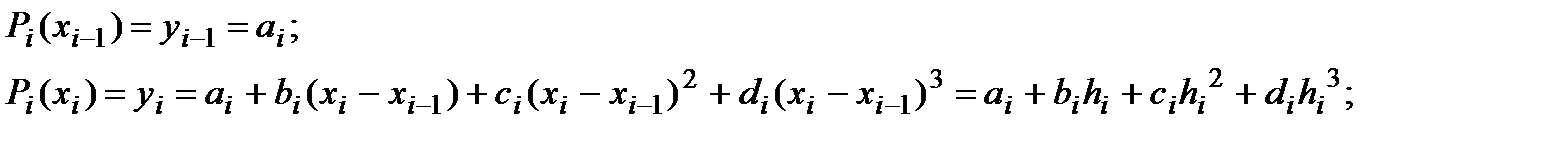
Через 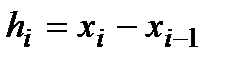 мы обозначили шаг между текущим и предыдущим узлами интерполяции.
мы обозначили шаг между текущим и предыдущим узлами интерполяции.
Итак, мы получили 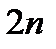 линейных алгебраических уравнений. Чтобы получить оставшиеся
линейных алгебраических уравнений. Чтобы получить оставшиеся 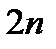 , потребуем непрерывности производных на отрезке
, потребуем непрерывности производных на отрезке 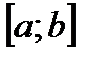 . Так как мы составляем сплайн 3 порядка с дефектом 1, то необходимо выполнить непрерывность
. Так как мы составляем сплайн 3 порядка с дефектом 1, то необходимо выполнить непрерывность 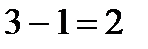 производных – первой
производных – первой 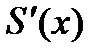 и второй
и второй 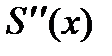 :
:
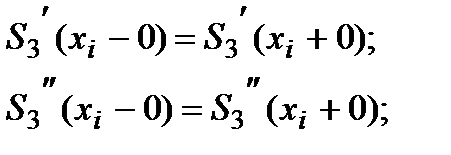
Обратите внимание, что эти условия должны выполняться только на внутренних точках, а не на крайних, поэтому внешние точки исключаем из рассмотрения:
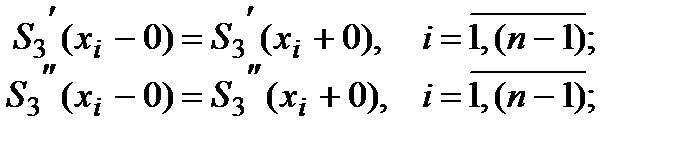
Считаем производные:
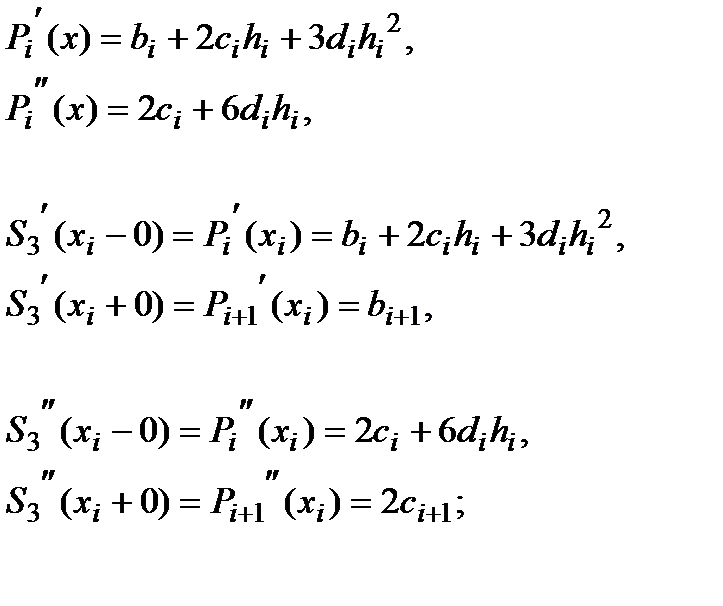
Приравнивая левые и правые соответствующие производные, получаем ещё 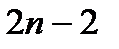 линейных алгебраических уравнений:
линейных алгебраических уравнений:
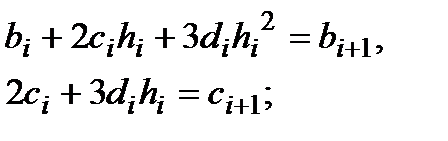
Недостаёт ещё двух уравнений, которыми мы должны описать поведение производных на крайних точках. Для их получения используют какие-либо требования к поведению сплайна в граничных точках интервала 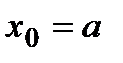 и
и 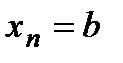 .
.
Выдвигаемые требования могут быть разные. Достаточно вторую производную в этих точках приравнять к каким-либо числам 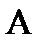 и
и 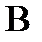 . Самое простое требование – это требование нулевой кривизны – положить эти числа равными нулю.
. Самое простое требование – это требование нулевой кривизны – положить эти числа равными нулю.
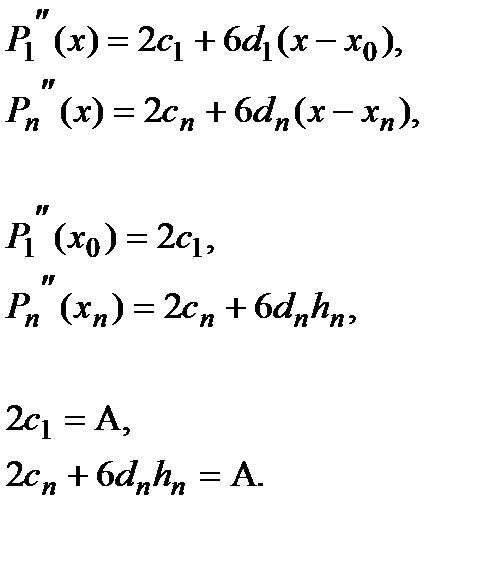
Теперь все 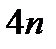 уравнений выведены и давайте соберём их в одну СЛАУ:
уравнений выведены и давайте соберём их в одну СЛАУ:
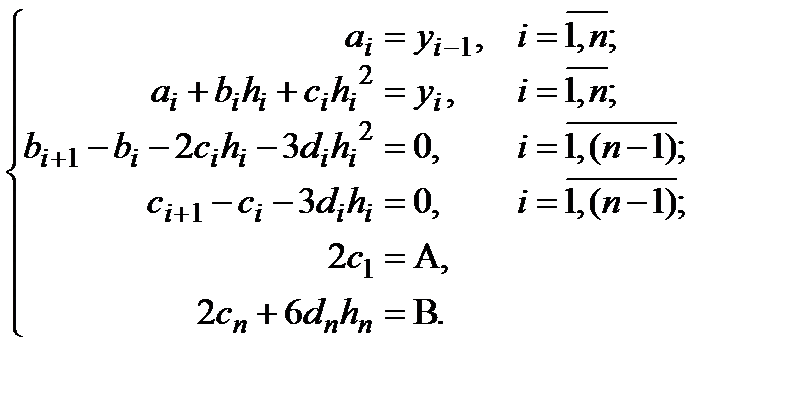
Исключим из этой системы 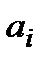 , так как они уже известны, и получим:
, так как они уже известны, и получим:
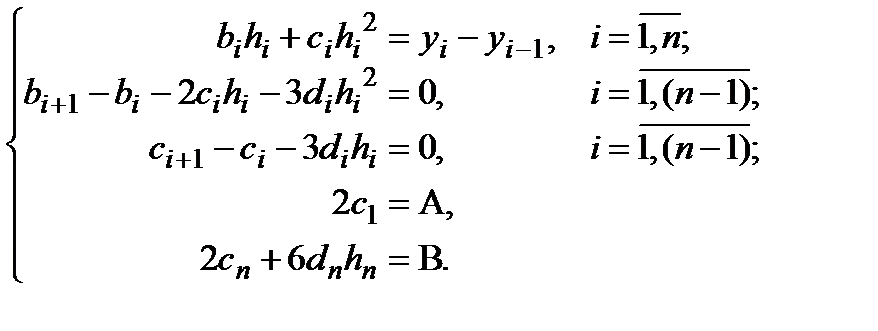
Эта система содержит все необходимые уравнения для получения 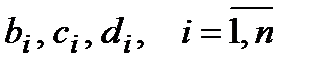 . Можно доказать, что решение этой СЛАУ существует.
. Можно доказать, что решение этой СЛАУ существует.
Задача 8.3.
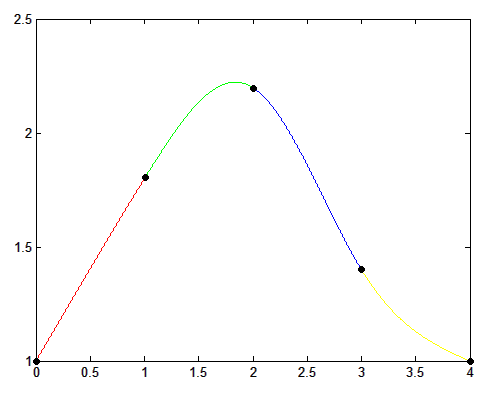
Функция задана таблицей:
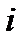
| 0 | 1 | 2 | 3 | 4 |
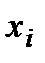
| 0 | 1 | 2 | 3 | 4 |
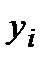
| 1.0 | 1.8 | 2.2 | 1.4 | 1.0 |
Составить систему уравнений для нахождения интерполяционного сплайна. Решить её и построить график полученного сплайна. На крайних точках применить требование нулевой кривизны.
Решение.
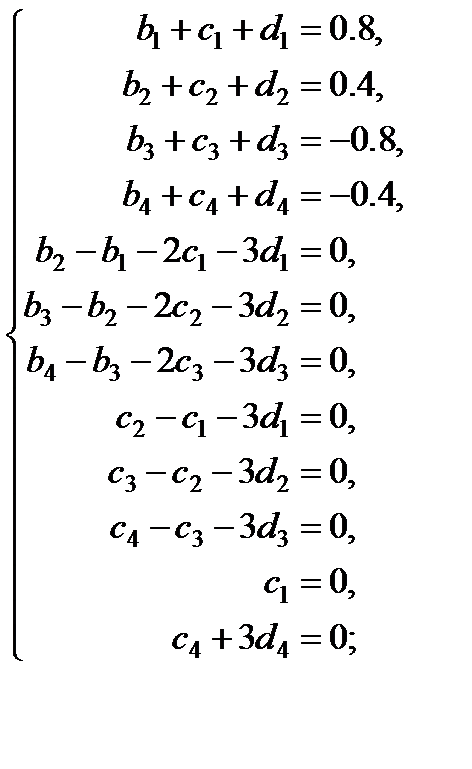
Так как 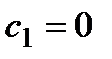 , то подставим его во все остальные уравнения и слегка упростим систему:
, то подставим его во все остальные уравнения и слегка упростим систему:
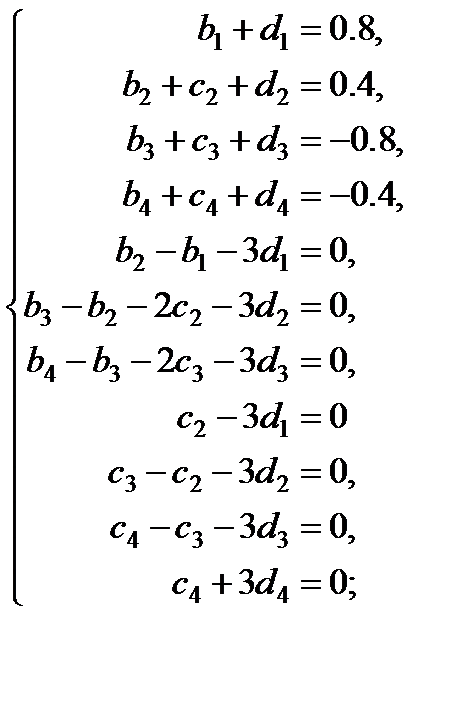
Итого получилась СЛАУ из 11 уравнений с 11 неизвестными:
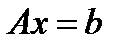

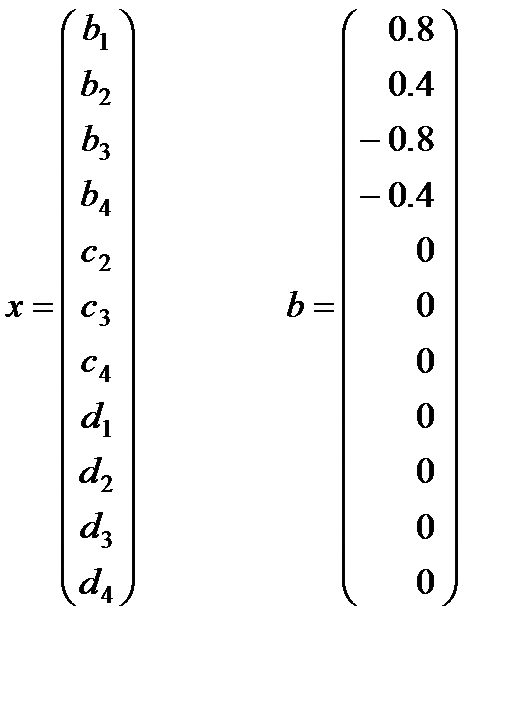
Использовав любой из описанных в предыдущих лекциях алгоритмов, получаем:

Искомый сплайн описывается следующим набором:
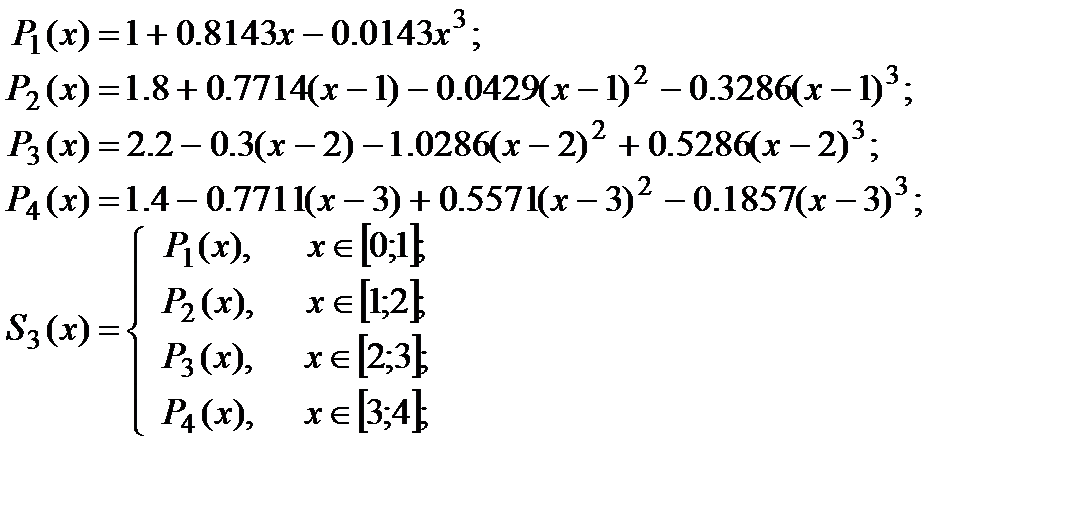
Дата: 2019-05-28, просмотров: 427.