Постановка задачи:
Необходимо вычислить
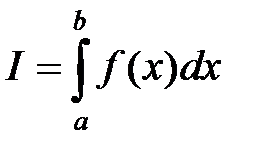
если 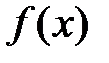 задана таблично.
задана таблично.
В подобных случаях применяют различные методы численного интегрирования. Формулы, используемые для приближенного вычисления однократных интегралов, называют квадратурными формулами. Один из приёмов построения квадратурных формул состоит в том, что подынтегральная функция 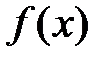 заменяется на отрезке
заменяется на отрезке 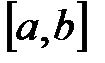 интерполяционным многочленом, например интерполяционным многочленом Лагранжа
интерполяционным многочленом, например интерполяционным многочленом Лагранжа 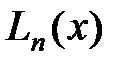 .
.
При этом полагают, что
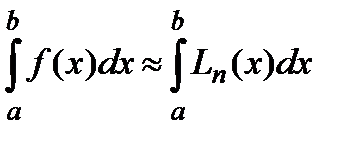 (1)
(1)
Используем представление:
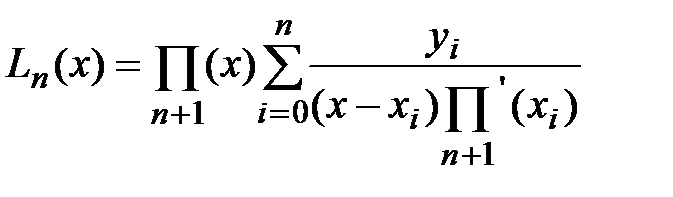 (2)
(2)
Получим:
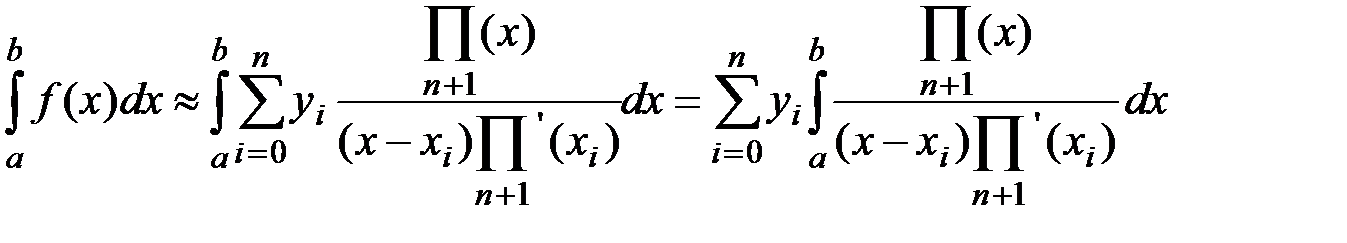 (3)
(3)
Т.о.
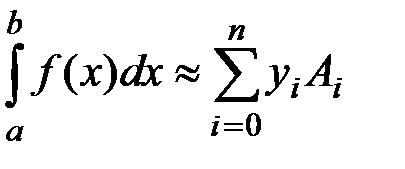 (3)
(3)
где
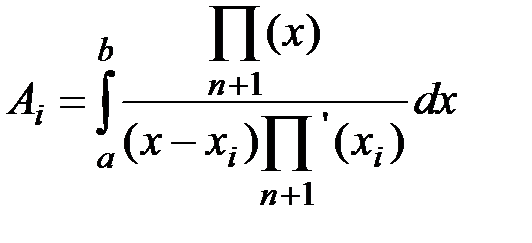 (4)
(4)
Замечание. Коэффициенты 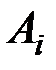 не зависят от функции
не зависят от функции 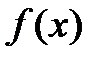 , т.к. они составлены только с учётом узлов интерполяции.
, т.к. они составлены только с учётом узлов интерполяции.
Предполагая, что шаг интерполяции постоянен, применяем формулу Лагранжа для равноотстоящих узлов и переходом к новой переменной 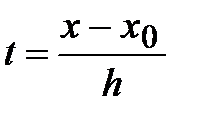 . С учётом того, что
. С учётом того, что 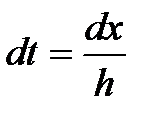 , формула (4) принимает вид:
, формула (4) принимает вид:
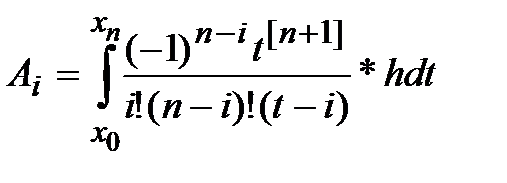 (5)
(5)
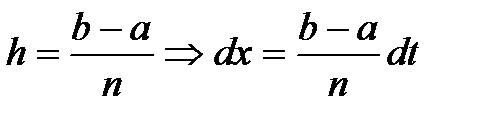
При 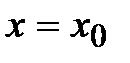 имеем
имеем 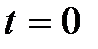 , а при
, а при 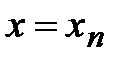 будет
будет 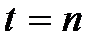 . Тогда:
. Тогда:
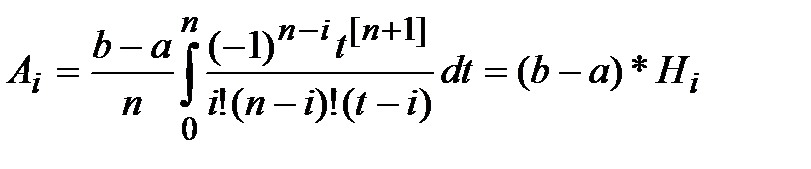 , (6)
, (6)
где
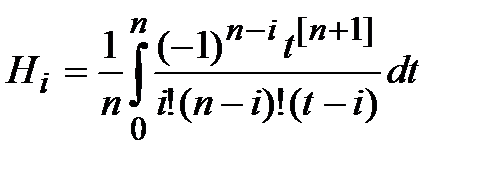 (7)
(7)
Окончательно, с учётом (3) и (4), получаем следующий вид квадратурных формул:
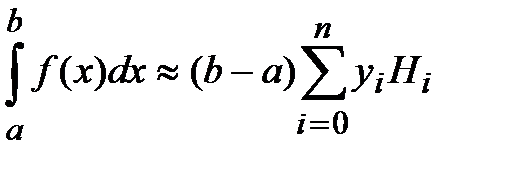 (8)
(8)
Формула (8) называется формулой Ньютона-Котса, дающей на интервале интегрирования  различные представления для различного числа
различные представления для различного числа 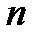 отрезков разбиения.
отрезков разбиения.
Формула трапеции
При 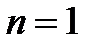 имеем
имеем 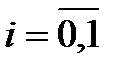 .
.
Тогда из (7) для формулы Ньютона-Котса получаем коэффициенты 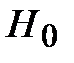 и
и 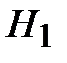 :
:
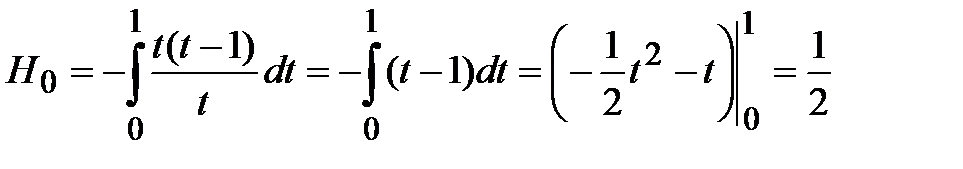 ;
;
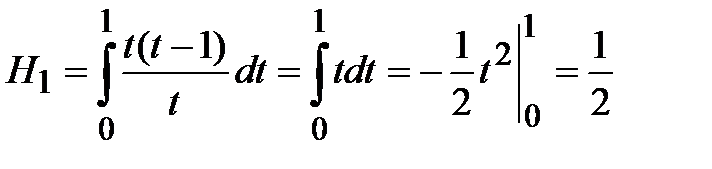 ;
;
И по формуле Ньютона-Котса (8) на  получаем:
получаем:
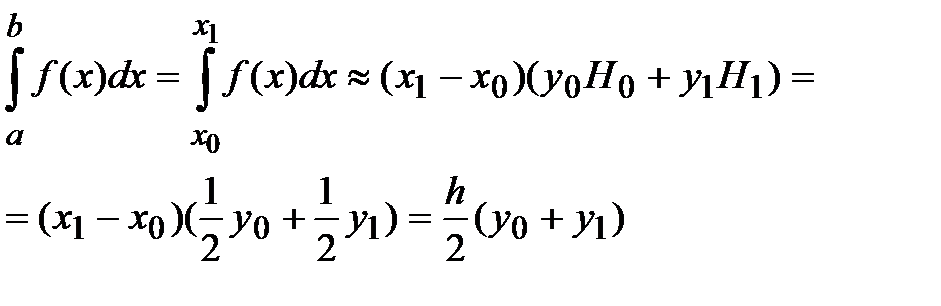
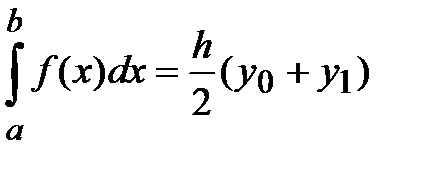 (9)
(9)
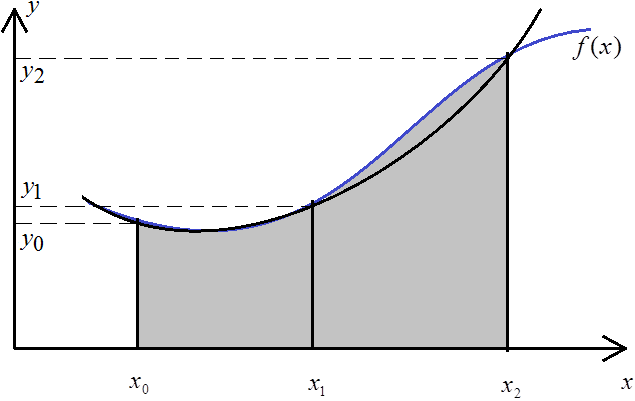
Это и есть формула трапеции – один из простейших способов вычисления определённого интеграла. При 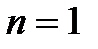 подынтегральная функция заменяется интерполяционным многочленом Лагранжа первой степени (т.е. линейной функции). Геометрически это означает, что площадь криволинейной фигуры
подынтегральная функция заменяется интерполяционным многочленом Лагранжа первой степени (т.е. линейной функции). Геометрически это означает, что площадь криволинейной фигуры  заменяется площадью проекции и величина интеграла составляет площадь трапеции – полусумма оснований, умноженная на высоту.
заменяется площадью проекции и величина интеграла составляет площадь трапеции – полусумма оснований, умноженная на высоту.
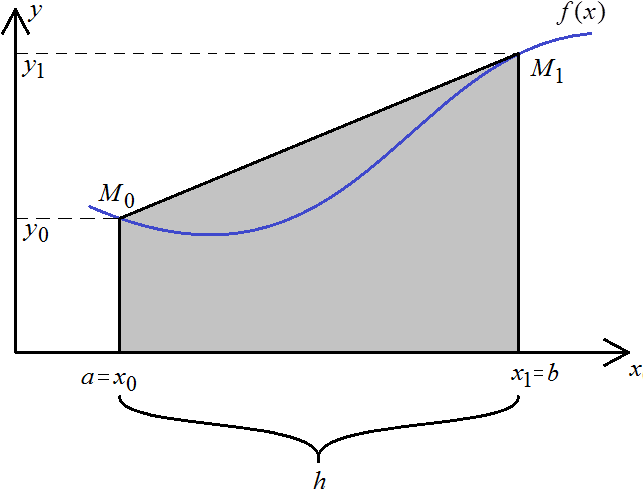
Естественно, при таком расчёте получается большая погрешность, но её легко можно уменьшить, разбив интервал на большее количество частей и считать каждый с помощью трапеции.
Формула Симпсона
Как известно, через три точки можно провести параболу.
При 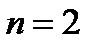 и
и 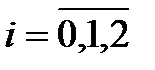 из (7) последовательно получим:
из (7) последовательно получим:
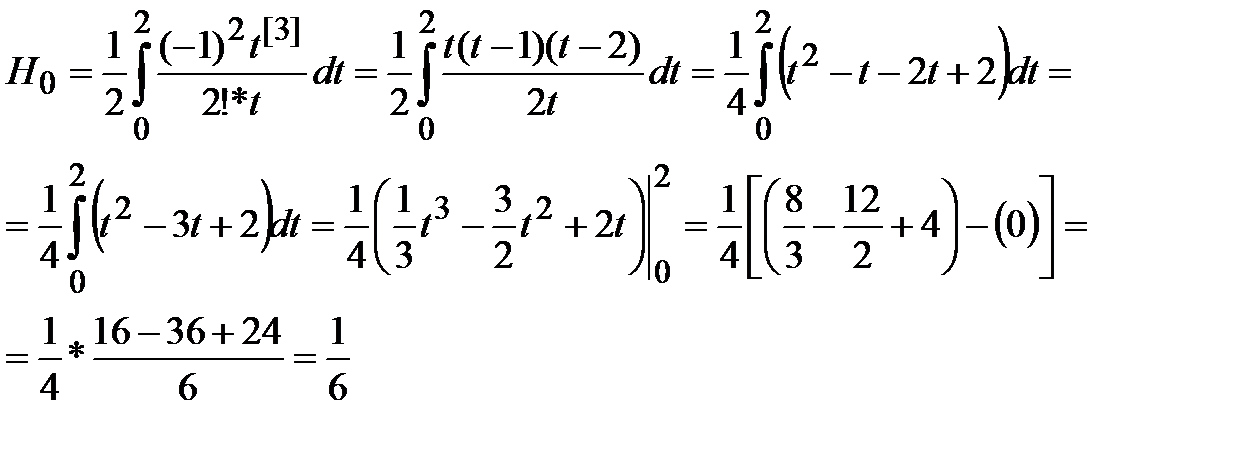
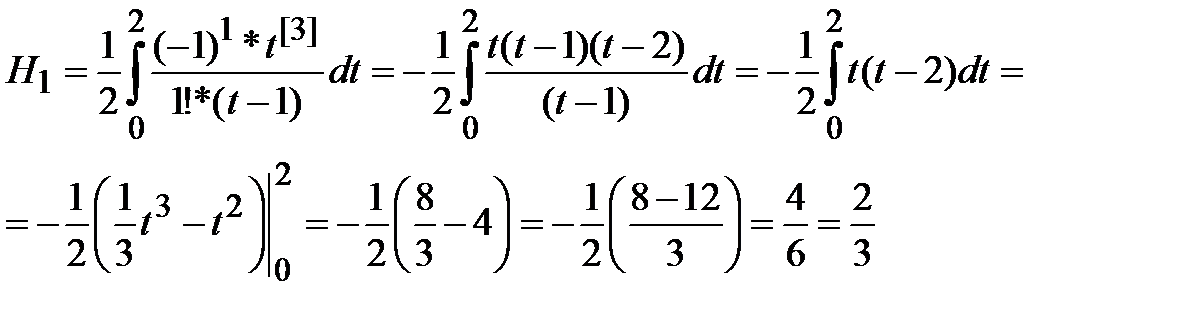
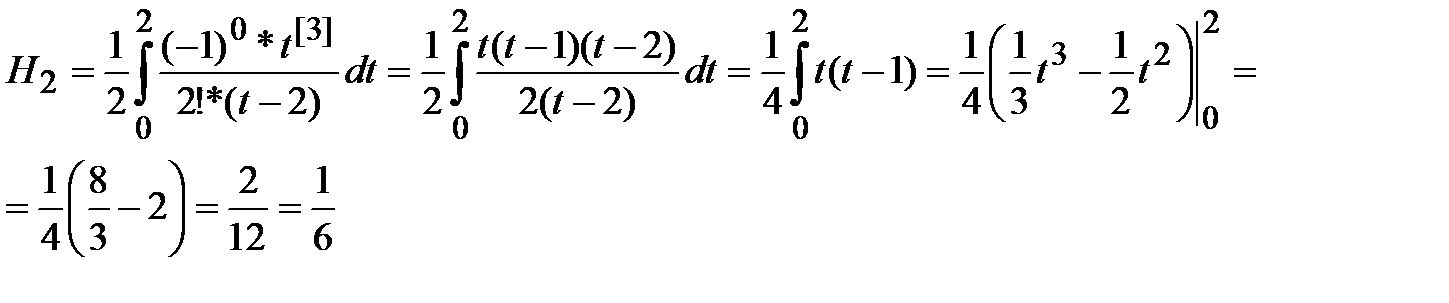
Тогда, с учётом (8), получаем:
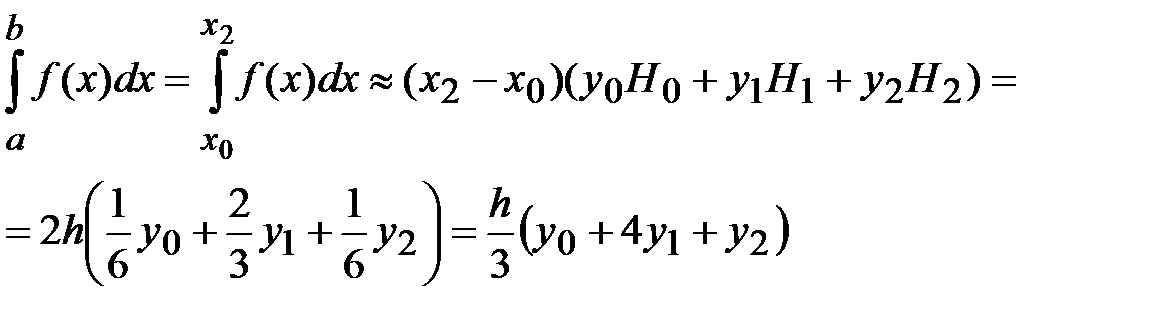
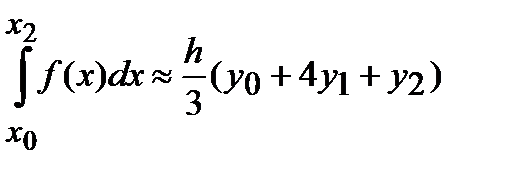 (10)
(10)
Это – формула Симпсона. Геометрически это означает то, что интегрируемая функция заменяется не на прямую, как в формуле трапеции, а на параболу, что даёт немного более точный результат:
Формула Симпсона 3/8
При 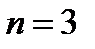 и
и 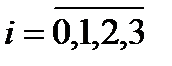 последовательно получим:
последовательно получим:
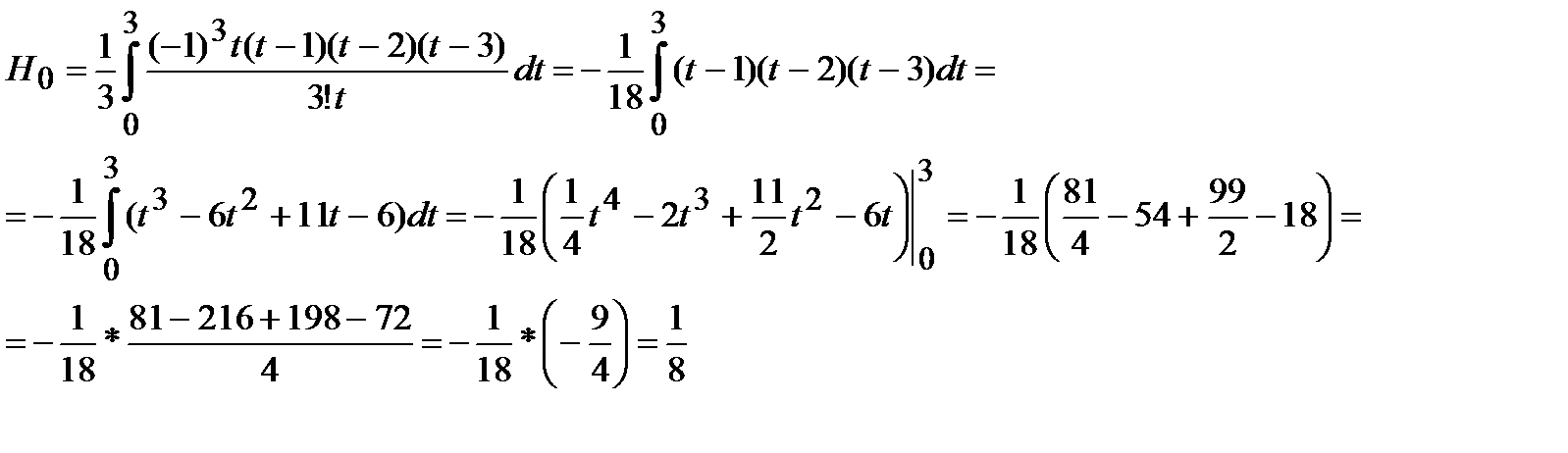
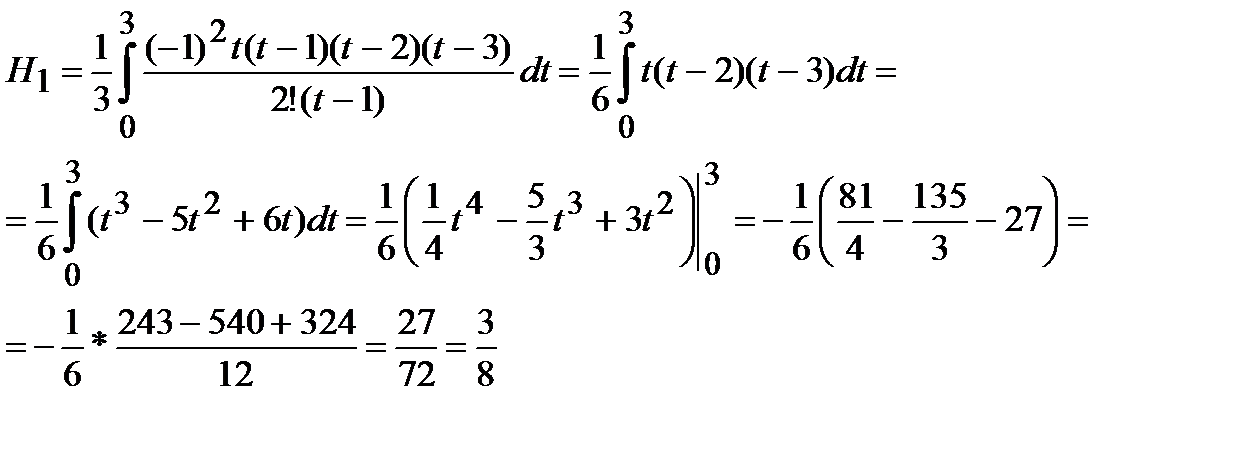
В конечном итоге получим:
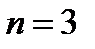 :
:
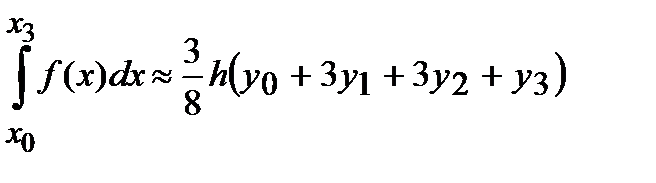
– формула Симпсона 3/8.
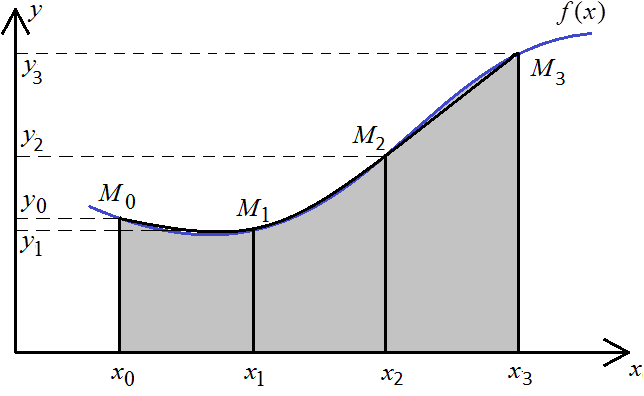
Геометрически это – кубическая парабола
Формула Буля
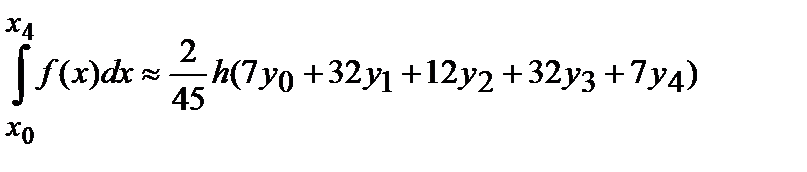
Задача.
Вычислить ОИ с помощью каждой из формул (кроме 3/8):
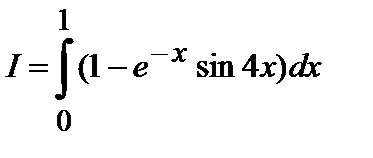
Рассчитать относительную погрешность каждого решения, если точное решение 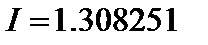 .
.
Решение. Предположим, что функция задана не аналитически, а с помощью набора дискретных значений с шагом 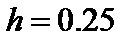 :
:
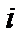
| 0 | 1 | 2 | 3 | 4 |
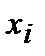
| 0 | 0.25 | 0.5 | 0.75 | 1 |
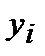
| 1 | 1.6553 | 1.5515 | 1.0666 | 0.7216 |
Формула трапеции.
Воспользуемся методом «разделяй и властвуй».
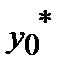
| 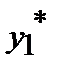
| 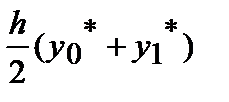
|
| 1 | 1.6553 | 0.3319 |
| 1.6553 | 1.5515 | 0.4009 |
| 1.5515 | 1.0666 | 0.3273 |
| 1.0666 | 0.7216 | 0.2235 |
| Сумма: | 1.2836 | |
Формула Симпсона
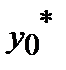
| 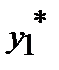
| 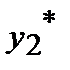
| 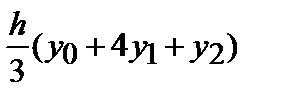
|
| 1 | 1.6553 | 1.5515 | 0.7644 |
| 1.5515 | 1.0666 | 0.7216 | 0.5450 |
| Сумма: | 1.3094 | ||
Формула Буля
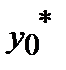
| 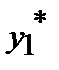
| 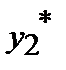
| 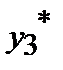
| 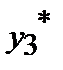
| 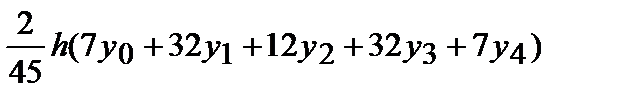
|
| 1 | 1.6553 | 1.5515 | 1.0666 | 0.7216 | 1.3086 |
Результат
| Точно | Формула Трапеции | Формула Симпсона | Формула Буля | |
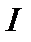
| 1.3083 | 1.2836 | 1.3094 | 1.3086 |
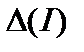
| - | 0.0247 | 0.0011 | 0.0003 |
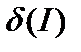
| - | 0.0189 | 0.0008 | 0.0002 |
Решение СНАУ
Надо решить систему уравнений:
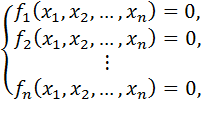 (1)
(1)
где 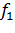 ,
, 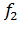 ,…,
,…, 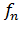 – заданные нелинейные функции. Среди них могут быть и линейные функции, но нелинейность хотя бы одной приводит к нелинейной системе уравнений. Поэтому система (1) называется нелинейной.
– заданные нелинейные функции. Среди них могут быть и линейные функции, но нелинейность хотя бы одной приводит к нелинейной системе уравнений. Поэтому система (1) называется нелинейной.
Систему (1) можно записать в векторном виде:
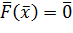 , (2)
, (2)
где
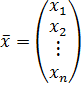 ,
, 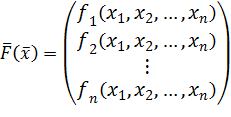 ,
, 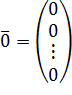 ,
,
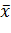 – вектор неизвестных,
– вектор неизвестных, 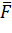 – нелинейная вектор-функция от вектора
– нелинейная вектор-функция от вектора 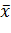 . Решением системы (2) называется вектор
. Решением системы (2) называется вектор 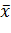 , при подстановке которого в систему (2) она превращается в тождество.
, при подстановке которого в систему (2) она превращается в тождество.
Наиболее употребительны для уточнения корней систем нелинейных уравнений – методы итерации (метод простой итерации и метод Зейделя) и метод Ньютона. Как и в случае уточнения корней одного нелинейного уравнения требуется определение хорошего начального приближения (отделение корня), гарантирующего сходимость метода и высокую скорость сходимости.
Для системы двух уравнений это может быть сделано графически, но для систем высоких порядков удовлетворительных методов отделения корней не существует.
В этих случаях можно использовать численные методы оптимизации – раздела вычислительной математики, выделяемого в самостоятельную дисциплину. Например, метод наискорейшего спуска или метод покоординатного спуска.
Дата: 2019-05-28, просмотров: 372.