Пусть требуется найти минимум 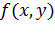 . Выберем нулевое значение
. Выберем нулевое значение 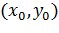 . Рассмотрим функцию одной переменной
. Рассмотрим функцию одной переменной 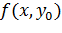 и найдем её минимум. Пусть этот минимум оказался в точке
и найдем её минимум. Пусть этот минимум оказался в точке 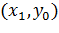 . Теперь точно так же будем искать минимум функции одной переменной
. Теперь точно так же будем искать минимум функции одной переменной 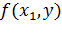 . Этот минимум окажется в точке
. Этот минимум окажется в точке 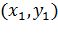 . Одна итерация спусков завершена. Будем повторять циклы, постепенно приближаясь ко дну котловины, пока не выполниться, например, условие
. Одна итерация спусков завершена. Будем повторять циклы, постепенно приближаясь ко дну котловины, пока не выполниться, например, условие 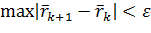 .
.
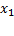
|
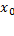
|
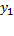
|
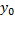
|
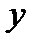
|
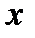
|
Сходимость метода зависит от вида функции и выбора нулевого (начального) приближения. Вблизи невырожденного минимума гладкой функции спуск по координатам линейно сходится к минимуму. Если линии уровня образуют истинный овраг, возможен случай, когда спуск по одной координате приводит на дно оврага, а любое движение последующей координате ведет на подъём. Процесс координатного спуска в данном случае не сходится к минимуму.
При попадании траектории спуска в разрешимый овраг сходимость становится чрезвычайно медленно. В физических задачах овражный рельеф указывает на то, что не учтена какая-то закономерность, определяющая связь между переменными. Явный учет этой закономерность облегчает использования численных методов.
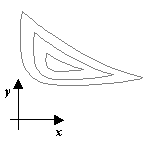
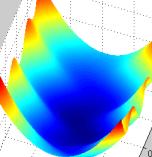
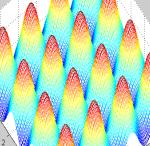
Виды рельефа:
| Котловинный (гладкая функция) | Истинный овраг | Разрешимый овраг | Неупорядоченный |
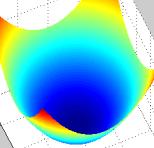
| 
| 
| 
|
Задача нелинейного программирования
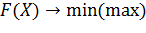 , (1)
, (1)
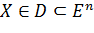
| (2а) (2b) |
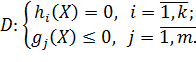
В (1), (2) хотя бы одна из функций 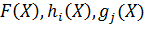 – нелинейная.
– нелинейная.
Необходимые и достаточные условия оптимальности
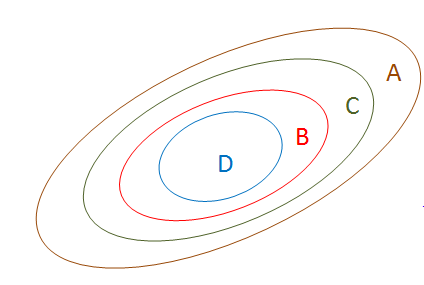

А – множество допустимых решений задачи (1), (2).
B – множество оптимальных решений задачи (1), (2).
С – множество допустимых решений, для которых выполняется необходимые условия оптимальности.
D – множество допустимых решений, для которых выполняется достаточные условия оптимальности.
Задача безусловной оптимизации
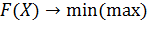 , (3)
, (3)
Теорема №1 (необходимое условие).
Пусть 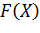 непрерывно дифференцируемая функция в точке
непрерывно дифференцируемая функция в точке 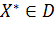 по
по 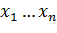 .
.
Если 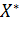 – локальное решение задачи (3), то
– локальное решение задачи (3), то
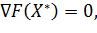 где (4)
где (4)
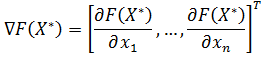
Стационарные точки.
Теорема 2 (достаточное условие).
Пусть:
1) 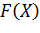 – дважды непрерывно дифференцируема в
– дважды непрерывно дифференцируема в 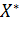 по
по 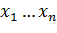 ;
;
2) 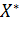 – стационарная точка.
– стационарная точка.
Для того чтобы 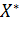 была решением задачи (3), достаточно, чтобы матрица Гессе Н в точке
была решением задачи (3), достаточно, чтобы матрица Гессе Н в точке 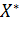 была:
была: 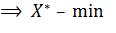
1) Положительно определенной ( 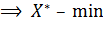 );
);
2) Отрицательно определенной ( 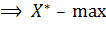 ).
).
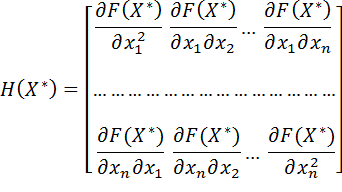
Теорема (Критерий Сильвестра).
Для того чтобы симметричная матрица Н была положительно определенной, необходимо и достаточно, чтобы все главные миноры матрицы были положительны:
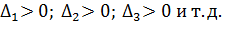
Для отрицательно определённых матриц знаки главных миноров чередуются, начиная со знака  для
для 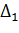 :
:
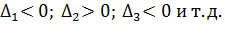
Замечание. Если Н знакоопределенная, то все её главные миноры 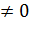 .
.
Дата: 2019-05-28, просмотров: 330.