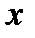
| 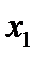
| 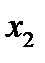
| … | 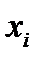
| … | 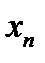
|
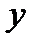
| 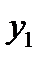
| 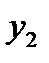
| … | 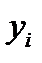
| … | 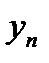
|
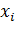 – цена нефти;
– цена нефти;
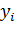 – индекс нефтяной компании.
– индекс нефтяной компании.
Требуется наилучшим образом отразить общую тенденцию зависимости 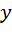 от
от 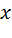 в виде эмпирической формулы:
в виде эмпирической формулы: 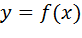 .
.
Используется МНК – метод наименьших квадратов.
Структура МНК.
Этап 1. Устанавливается общий вид зависимости 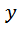 от
от 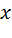 :
:
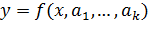
Например,
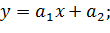
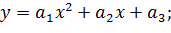
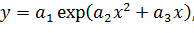
и так далее.
Строится функция:
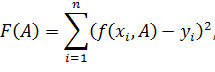
| (5) |
где 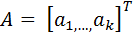 – вектор неизвестных параметров.
– вектор неизвестных параметров.
Этап 2.
Решается задача безусловной оптимизации:
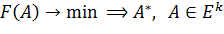 (6)
(6)
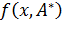 – наилучшая кривая в смысле:
– наилучшая кривая в смысле:
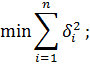
Задача:
Пусть 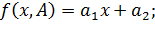
| Тогда: | 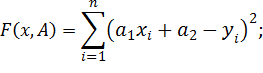
|
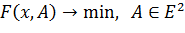 ; (7)
; (7)
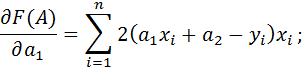
|
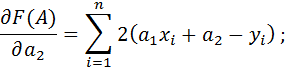
|
Необходимые условия оптимальности:
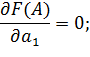
|
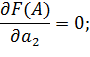
|
Получили систему уравнений:

| (8) |
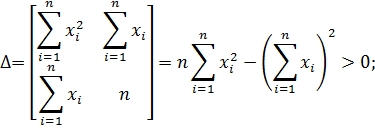
Матрица Гессе .
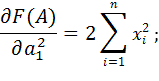
|
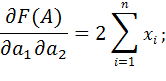
|
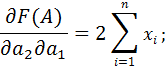
|
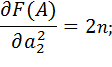
|
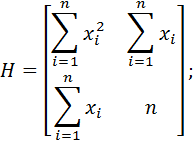
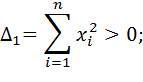
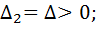
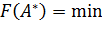 в задаче (7).
в задаче (7).
Численные методы безусловной оптимизации.
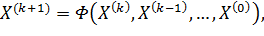 (9)
(9)
где 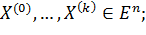
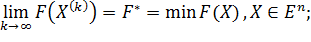
| (10) |
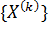 – минимизирующая последовательность;
– минимизирующая последовательность;
| Если | 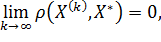
| (11) |
то говорят, что 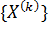 сходится к
сходится к 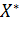 ;
;
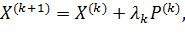
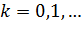 (12)
(12)
где 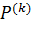 – направление поиска точки
– направление поиска точки 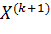 из
из 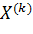 ;
;
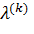 – шаговая длина в направлении
– шаговая длина в направлении 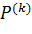 ;
;
Критерий точности:
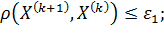 (14.1)
(14.1)
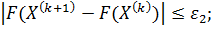 (14.2)
(14.2)
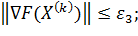 (14.3)
(14.3)
Прямые методы безусловной оптимизации. Циклический покоординатный спуск.
Шаг 0: Выбор начального приближения 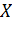 . Выбор
. Выбор 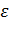 >0, а также критерия (14). Вычисление
>0, а также критерия (14). Вычисление 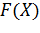 ; Положить j =1.
; Положить j =1.
Шаг 1: Решить задачу одномерной минимизации: 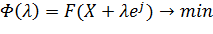 (15), где
(15), где 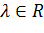 . В результате находим
. В результате находим 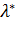 . Положить
. Положить 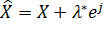 . Вычислить
. Вычислить 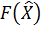 .
.
Шаг 2: Если 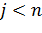 , то положить
, то положить 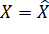 ;
; 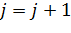 и перейти к шагу 1. Иначе – перейти к шагу 3.
и перейти к шагу 1. Иначе – перейти к шагу 3.
Шаг 3: Проверка условия достижения точности 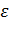 (критерий останова):
(критерий останова): 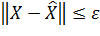 или
или 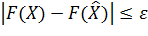 . Если она выполняется, то положить
. Если она выполняется, то положить 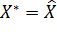 ;
; 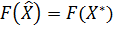 и Stop. Иначе положить:
и Stop. Иначе положить: 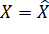 ;
; 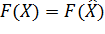 ;
; 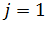 . Переход к шагу 1.
. Переход к шагу 1.
Метод параболической интерполяции.
Используется для решения вспомогательной задачи одномерной минимизации на шаге 1.
Выбираем:
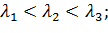
Вычисляем:
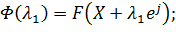
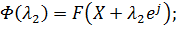
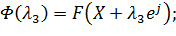
Полагаем:
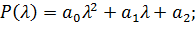 (16)
(16)
Для 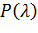 должны выполняться требования:
должны выполняться требования:
| (17) |
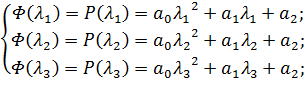
Решаем (17) относительно 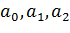 .
.
Получаем аналитическое выражение для 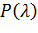 .
.
(17) всегда имеет единственное решение, т.к.
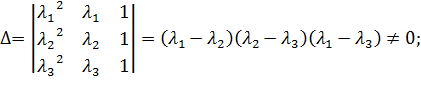 (18)
(18)
(18) – определитель Вандермонда.
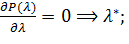
– приближенное решение задачи (15).
Задача 1.
Рассмотри систему нелинейных уравнений:
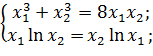
Найти методом покоординатного спуска корни данной системы, если начальное приближение 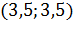 ;
; 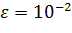 .
.
Решение.
Для начала составим целевую функцию:
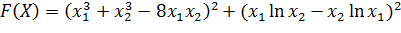 ;
;
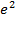
|
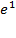
|
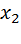
|
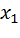
|
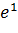 ,
, 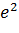 – базисные векторы;
– базисные векторы;
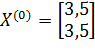 – начальное приближение;
– начальное приближение; 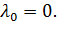
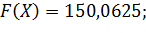
1 ) Пусть 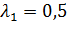 ;
; 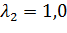 .
.
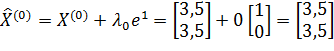 ;
;
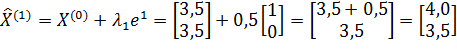 ;
;
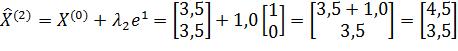 ;
;
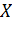
| 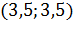
| 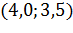
| 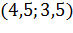
|
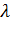
| 0 | 0,5 | 1,0 |
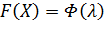
| 150,0625 | 26,2909 | 64,1393 |
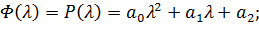
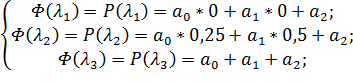
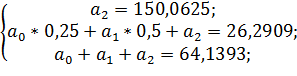
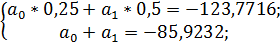
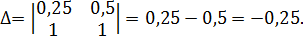
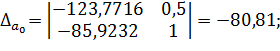
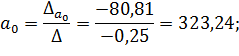
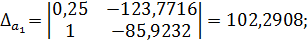
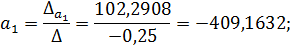
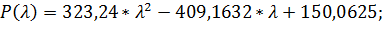
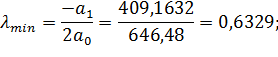
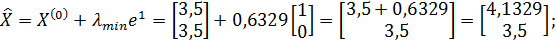
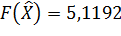 ;
;
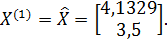
2) Пусть 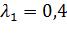 ;
; 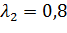 .
.
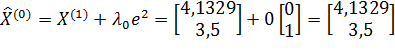 ;
;
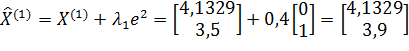 ;
;
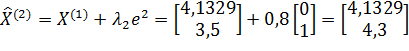 ;
;
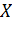
| 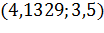
| 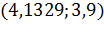
| 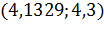
|
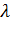
| 0 | 0,4 | 0,8 |
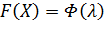
| 5,1192 | 0,9414 | 62,8702 |
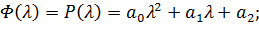
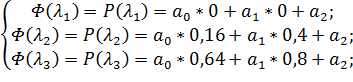
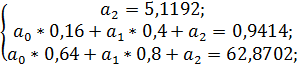
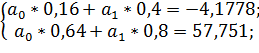
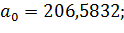
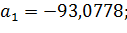
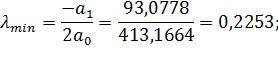
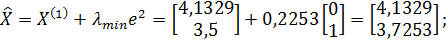
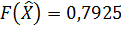 ;
;
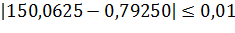 – Не выполняется!
– Не выполняется!
⟹ 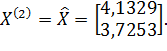
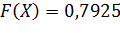 ;
;
3) Пусть 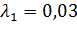 ;
; 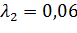 .
.
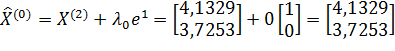 ;
;
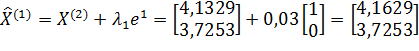 ;
;
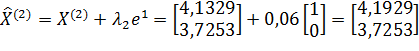 ;
;
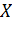
| 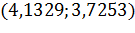
| 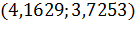
| 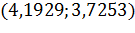
|
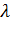
| 0 | 0,03 | 0,06 |
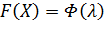
| 0,7925 | 0,076 | 0,2362 |
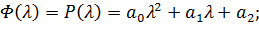
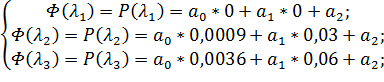
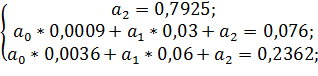
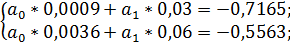
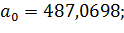
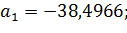
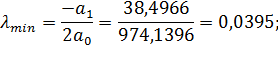
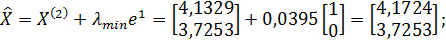
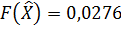 ;
;
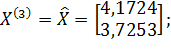
4) Пусть 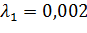 ;
; 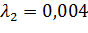 .
.
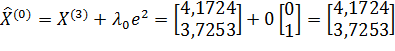 ;
;
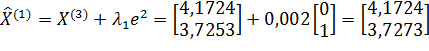 ;
;
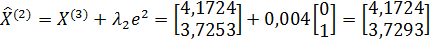 ;
;
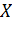
| 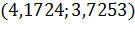
| 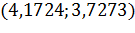
| 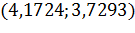
|
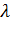
| 0 | 0,002 | 0,004 |
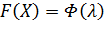
| 0,0276 | 0,0273 | 0,0275 |
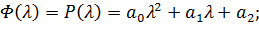
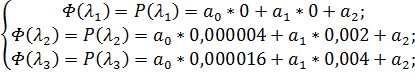
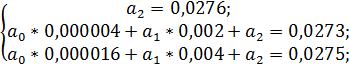
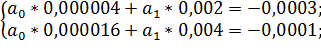
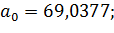
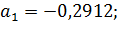
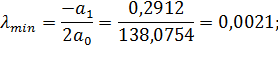
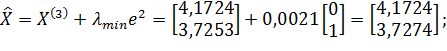
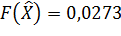 ;
;
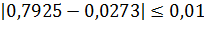 – Не выполняется!
– Не выполняется!
⟹ 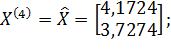
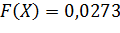 ;
;
Следующие итерации будут без описания.
5) 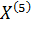 =
= 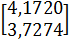 при
при 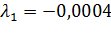 ;
; 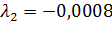 .
.
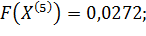
6) 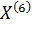 =
= 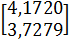 при
при 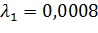 ;
; 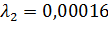 .
.
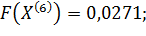
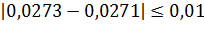 – Выполняется!
– Выполняется!
Так как критерий останова выполнился, то 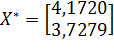 .
.
Проверка :
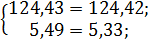
Следовательно, 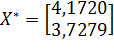 является решением системы нелинейных уравнений.
является решением системы нелинейных уравнений.
Схематичное смещение корней на плоскости после каждой итерации:
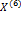
|
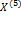
|
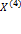
|
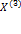
|
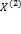
|
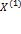
|
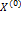
|
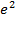
|
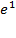
|
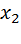
|
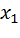
|
Ответ: 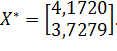
.
Численное решение дифференциальных уравнений
Дата: 2019-05-28, просмотров: 319.