Вычислительная задача:
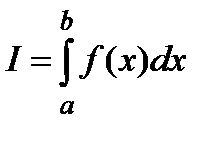
Попробуем определить её обусловленность.
Пусть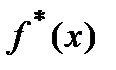 
- приближённо заданная интегрируемая функция и её интеграл равен 
.
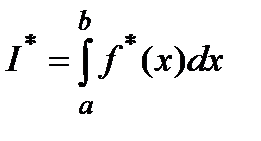Определим абсолютную погрешность функции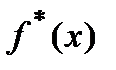 
с помощью равенства:
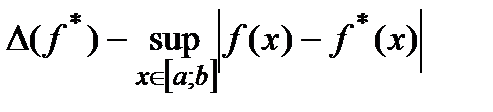(8)
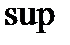- это «супремум» - «точная верхняя грань». Супремумом подмножества X упорядоченного множества M называется такой элемент 
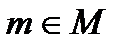, который больше либо равен всем элементам множества X.
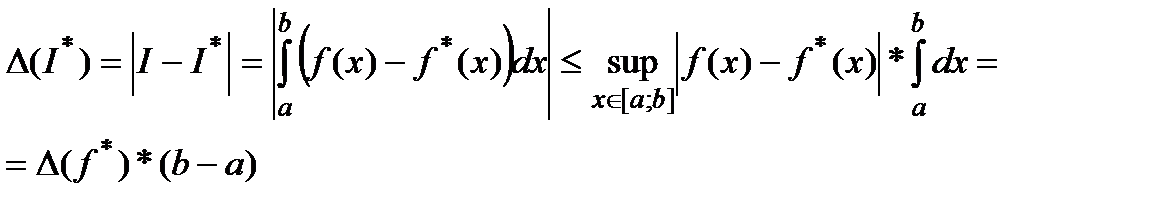(9)
Тогда абсолютное число обусловленности равно
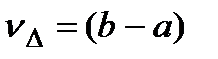(10)
Теперь посчитаем относительное число обусловленности.
Положим
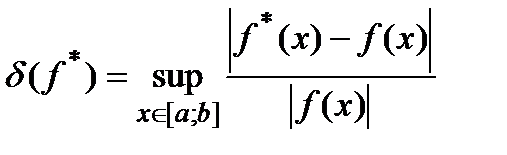. (11)
Тогда используя неравенство, получаем:
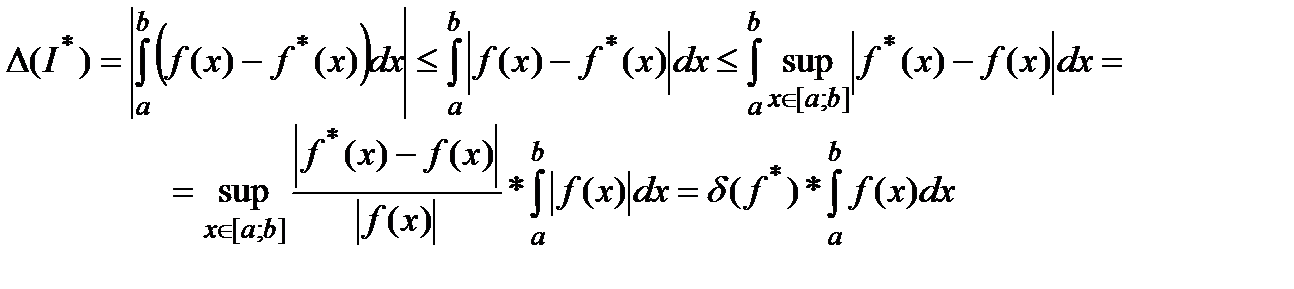
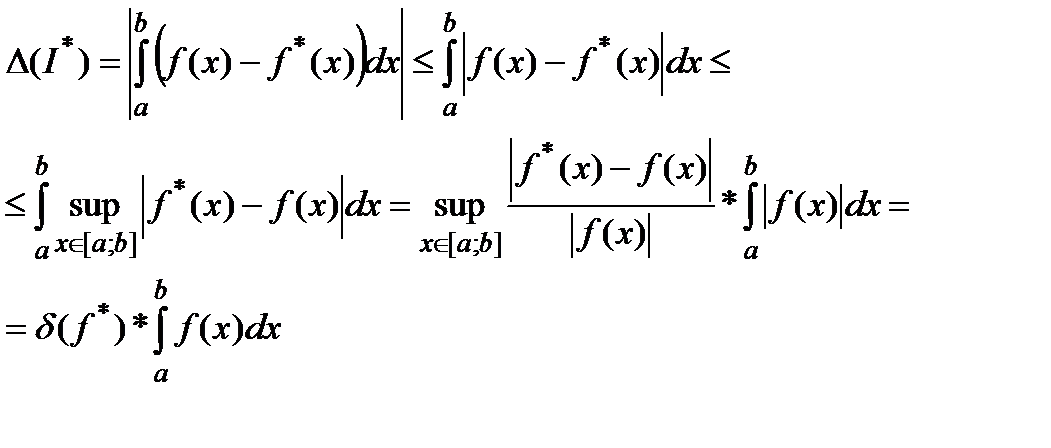(12)
То есть
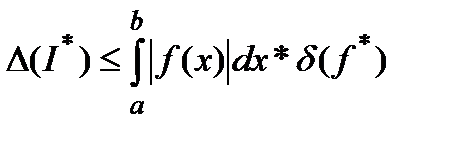(13)
Тогда
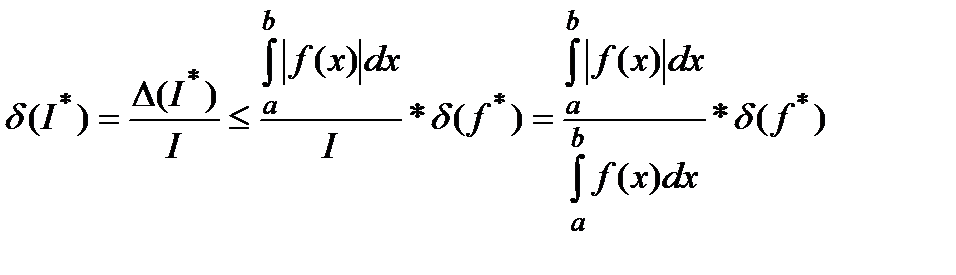
Тогда относительное число обусловленности равно:
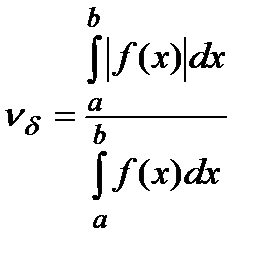
Выводы.
1. Если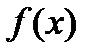 
знакопостоянна на 
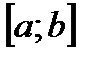, то 
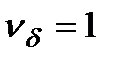, и задача вычисления определённого интеграла хорошо обусловлена.
2. Если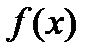 
на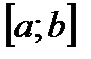 
принимает значения разных знаков, то 
.
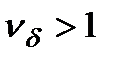3. Если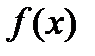 
не является сильно осциллирующей (относительно нуля) функцией на отрезке 
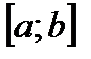, то 
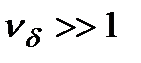и задача является плохо обусловленной.
Обусловленность задачи решения СЛАУ
Рассмотрим СЛАУ:
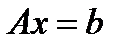(1)
Предположим, что элементы A заданы точно, а вектор-столбец b – приближённо.
Пусть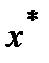 
- приближённое решение СЛАУ (1), 
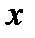- точное решение СЛАУ (1).
Тогда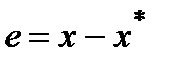 
- абсолютная погрешность решения СЛАУ (1).
Невязка – это погрешность в результате вычислений:
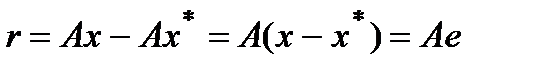
Погрешность e и невязка r связаны соотношением
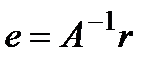(2)
Абсолютные и относительные погрешности вектора:
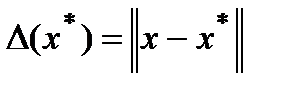(3а)
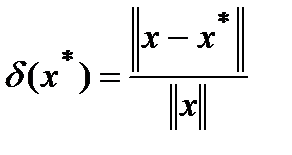(3б)
Лемма. Для погрешности приближённого решения СЛАУ (1) справедлива следующая оценка:
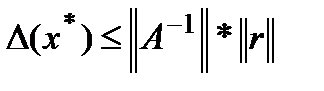(4)
где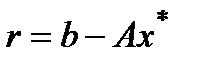 
– невязка, соответствующая 
.
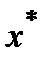Доказательство.
.
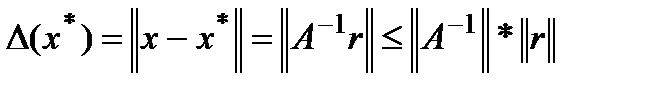Последнее преобразование согласно свойству нормы
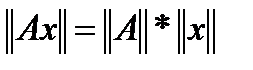
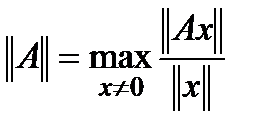
Теорема. Пусть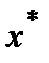 
- точное решение системы 
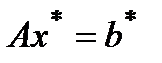(замечание: 
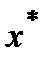– приближенное решение СЛАУ 
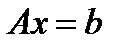) , в которой 
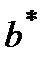является приближением к 
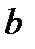. Тогда верны следующие оценки абсолютной и относительной погрешностей:
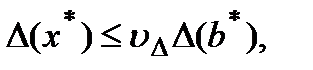(5)
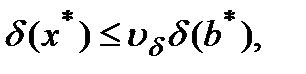(6)
где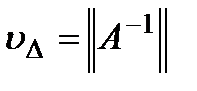 
- абсолютное число обусловленности, 
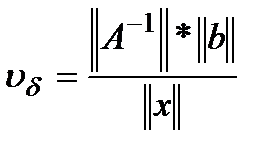- относительное (естественное) число обусловленности, которое зависит от 
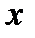и характеризует коэффициент возможного возрастания относительной погрешности решения 
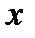, вызванном погрешностью задания правой части.
Вычислим максимальное значение естественного числа обусловленности, используя определение нормы матрицы:
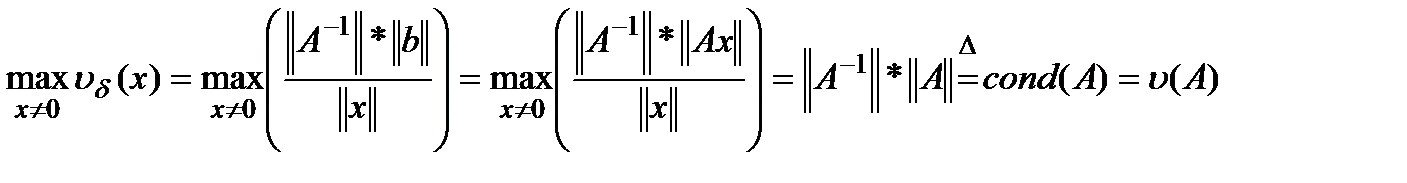
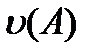, также обозначаемое как 
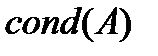(сокр. от «condition number»)
- стандартное число обусловленности матрицы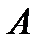 
.
Следствие. Справедлива оценка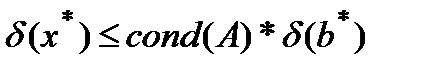 
.
Если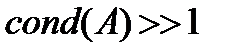 
, то СЛАУ плохо обусловлена, то есть существует такое решение СЛАУ, которое обладает чрезвычайно высокой чувствительностью к малым погрешностям правой части СЛАУ 
.
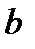Задача 7.1.
Рассмотрим СЛАУ:
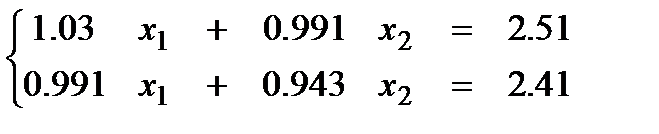(7)
Решение этой СЛАУ с точностью до трёх знаков:
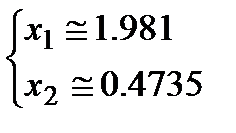
Предположим, что вектор правых частей
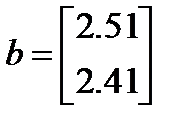
получен не точно, а с погрешностью. Пусть он определён с точностью до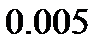 
. Сделаем возмущения:
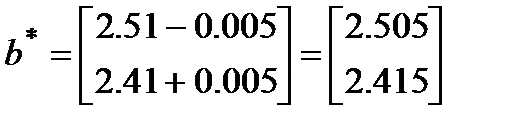
Решением системы, соответствующим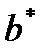 
, является
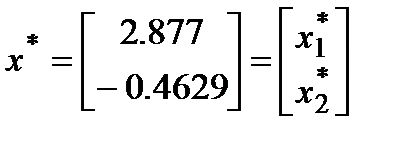
Вычислим относительную погрешность задания правой части:
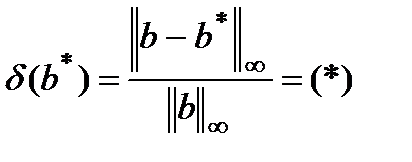
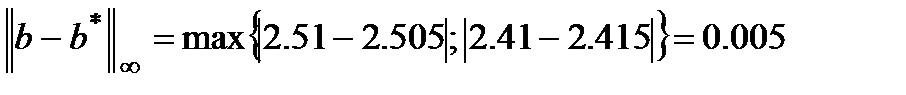
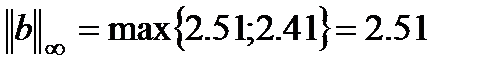
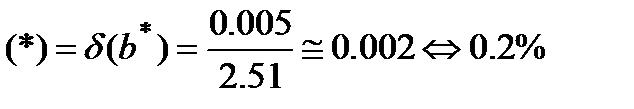
Относительная погрешность решения, соответствующая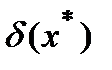 
:
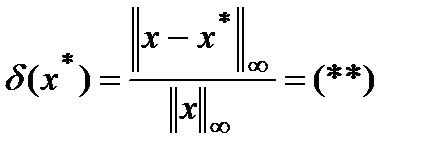
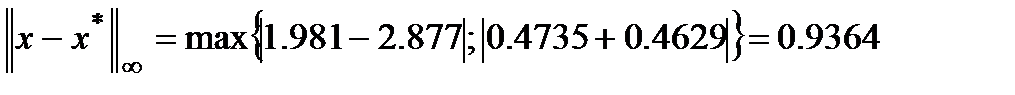
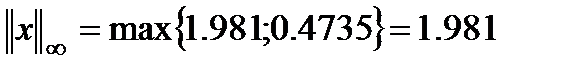
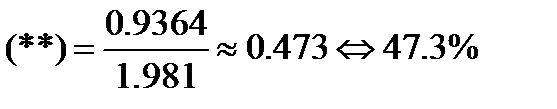
Таким образом погрешность возросла в
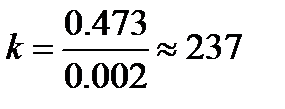раз.
Вычислим стандартное число обусловленности:
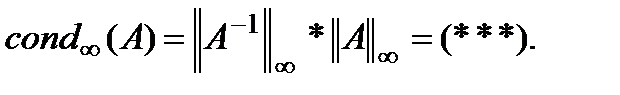
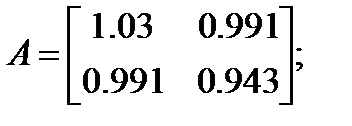
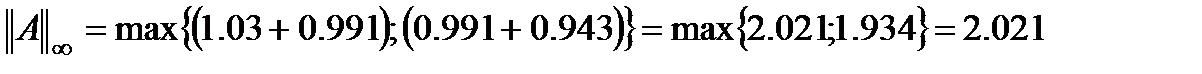
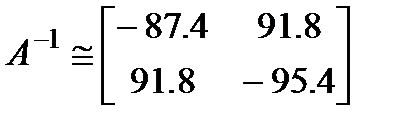
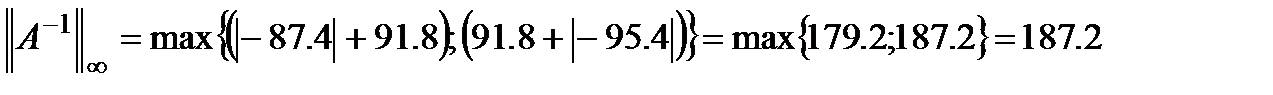
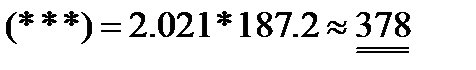
Геометрическая интерпретация:
Первому уравнению в (7) соответствует прямая:
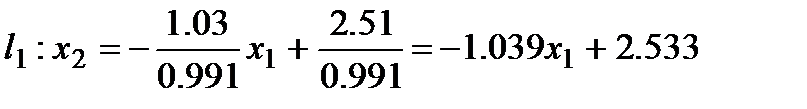
Второму уравнению в (7) соответствует прямая:
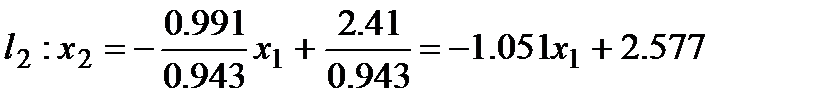
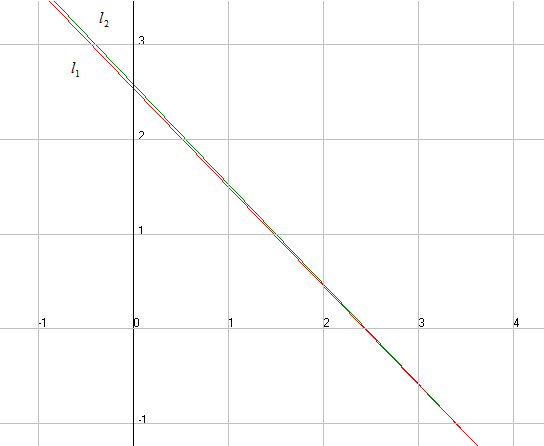
Методы интерполяции
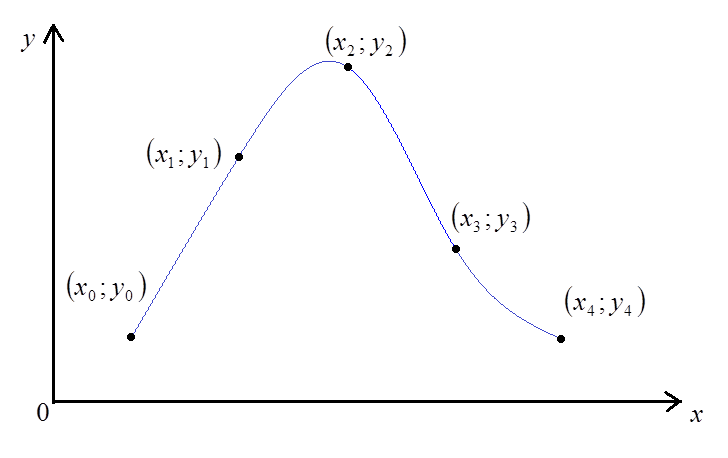
Интерполяция – это задача нахождения промежуточных значений величины по имеющемуся дискретному набору значений.
Пусть функция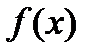 
задана таблицей n значений:
| 
| 
| 
| 
|
| 
| 
| 
| 
|
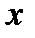
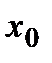
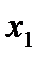
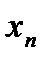
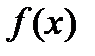
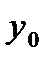
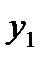
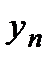
То есть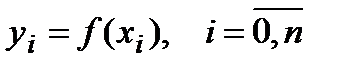 
.
Точки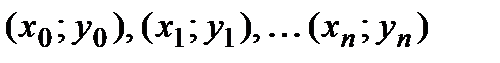 
называются интерполяционными узлами.
Задача интерполяции состоит в том, чтобы вычислить значение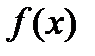 
в точке 
.
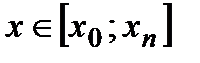Решается эта задача построением по исходной информации из таблицы функции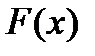 
, которая близка к 
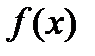и имеет аналитическое представление. После этого предполагается, что 
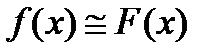, и 
и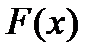спользуется для получения неизвестного значения 
.
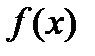Классическая постановка задачи интерполяции состоит в построении такой функции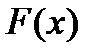 
, что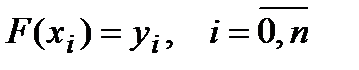 
.
Дата: 2019-05-28, просмотров: 461.
