Критерий окончания итерационного процесса формулируется на основе апостериорной оценки погрешности.
Теорема. Пусть выполнено условие предыдущей теоремы. Тогда верна следующая апостериорная оценка погрешности:
, 
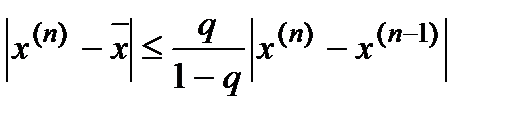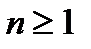
Отсюда следует, что вычисление следует продолжать до выполнения условия:
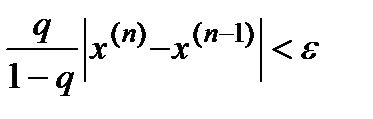
или
|
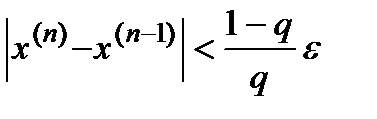
Пример. Решить уравнение методом простой итерации с точностью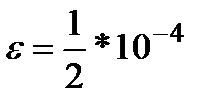 
.
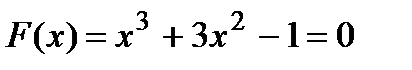
1. Локализуем корни уравнения. Для этого построим таблицу:
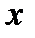
| -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| - | - | + | + | - | + | + | + |
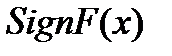
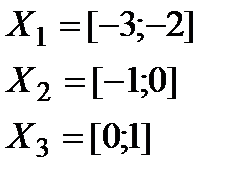
Будем искать корень на отрезке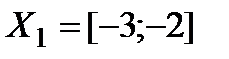 
. Т.к. на 
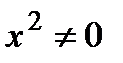, то разделим обе части уравнения на 
:
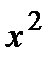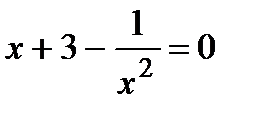
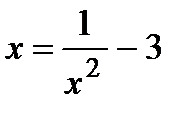
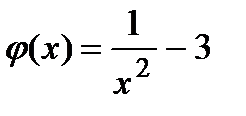
Проверим выполнение условий теоремы о достаточных условиях:
, 
, 
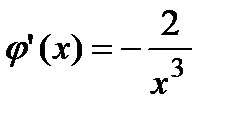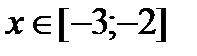
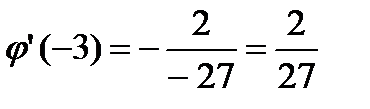
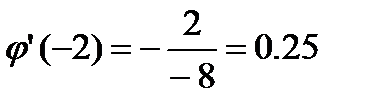
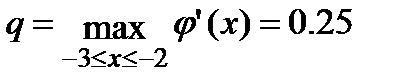
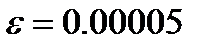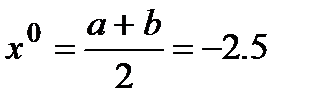
Построим таблицу:
| 
| 
|
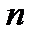
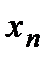
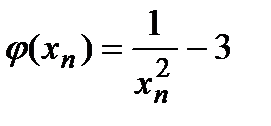
| 0 | -2.50000 | -2.84000 |
| 1 | -2.84000 | -2.87602 |
| 2 | -2.87602 | -2.87910 |
| 3 | -2.87910 | -2.87936 |
| 4 | -2.87936 | -2.87938 |
| 5 | -2.87938 | -2.87938 |
Т.е. критерием останова является выполнение условия:
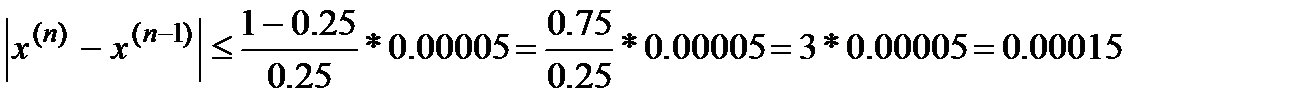
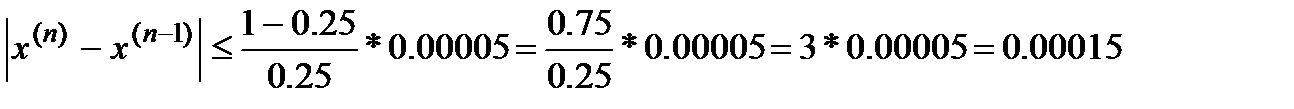
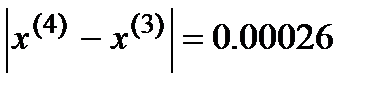
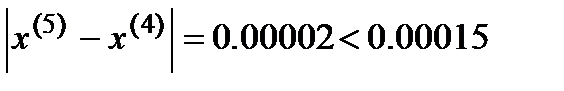
1.4. Преобразование уравнения к итерационному виду
Уравнение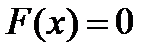 
может быть приведено к виду 
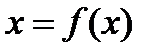различными способами. Однако это следует делать таким образом, чтобы выполнялись условия теоремы.
Эквивалентное преобразование уравнения
(1)
к виду:
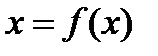(2)
При этом такое преобразование имеет смысл в том случае, когда выполняется условие
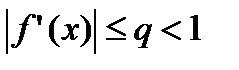(3)
Предположим, что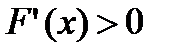 
и непрерывна на 
.
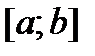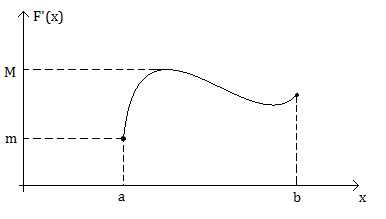
Тогда существуют положительные постоянные m и M такие, что
, 
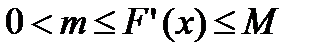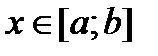
Приведём уравнение (1) к виду:
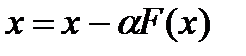, (4)
где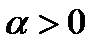 
. При этом итерационная функция 
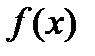имеет вид:
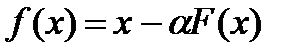(5)
Требуется выбрать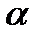 
так, чтобы выполнялось условие (3). Причём q должно быть по возможности минимальным, что обеспечит более высокую скорость сходимости итерационного процесса
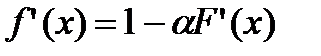
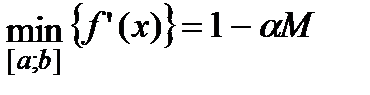
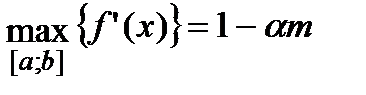
Поэтому справедливо:
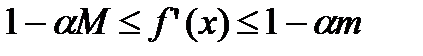(6)
Следовательно,
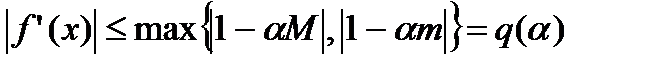(7)
Для того, чтобы выполнялось равенство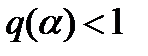 
, достаточно выбрать любые 
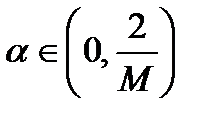. Действительно, представим 
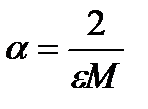в виде:
, где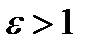 
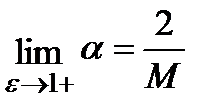
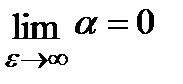
Т.е.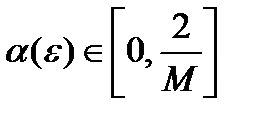 
Тогда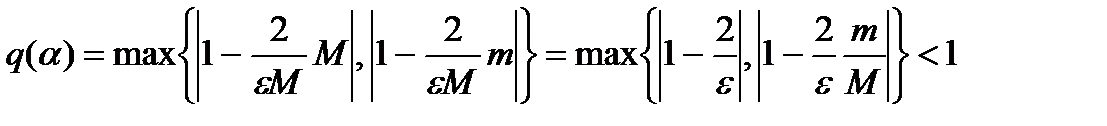 
Если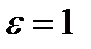 
, то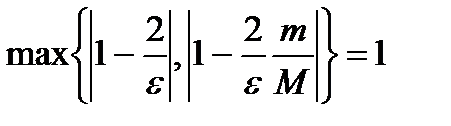 
Если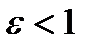 
, то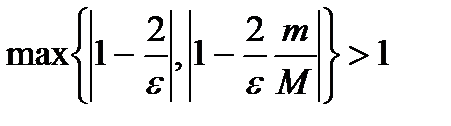 
Конкретный выбор параметра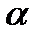 
зависит от наличия информации о числах m и M.
1) Если m и M известны, то наилучшим является выбор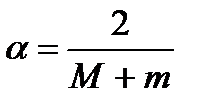 
.
В этом случае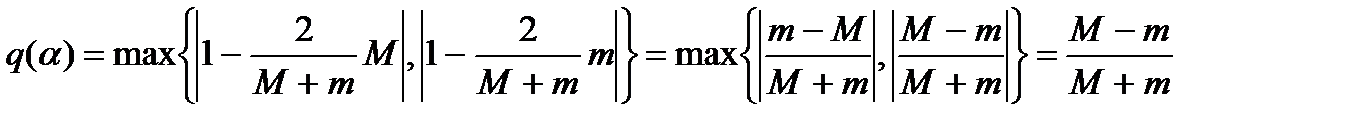 
2) Если известно только M, то можно положить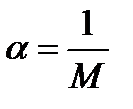 
.
В этом случае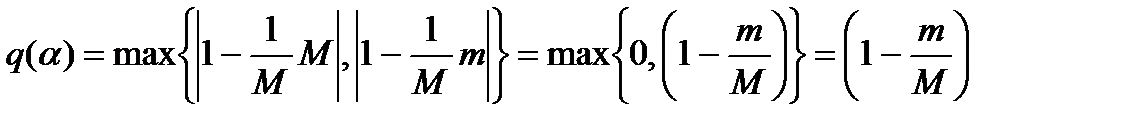 
Замечание: Если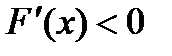 
на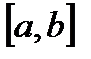 
, то этот случай сводится к рассмотренному выше умножением уравнения 
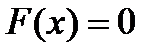на -1:
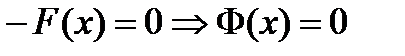, где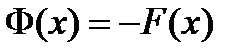 
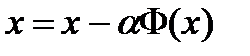
Пример: Приведём к итерационному виду уравнение:
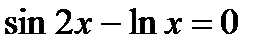
Уточнить корень на отрезке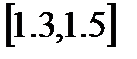 
Ответ: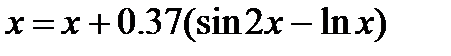 
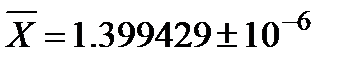
Вычисление алгебраического полинома.
Большое прикладное значение имеет задача вычисления алгебраического полинома:
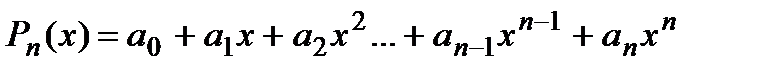
Напомним, что полином степени n имеет ровно n корней, как и действительных, так и комплексных.
Для того, чтобы вычислить корни таких уравнений можно с успехом применять итерационные процедуры, например метод Ньютона-Рафсона. Но их применение чаще всего приводит к выполнению множества действий, что может привести к потере точности и увеличению времени работы.
Один из эффективных способов вычисления алгебраического полинома – использование схемы Горнера.
Схема Горнера
Рассмотрим этот метод на примере полинома пятого порядка:
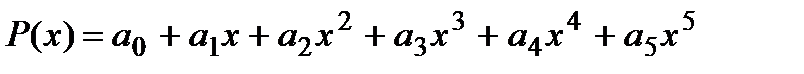
Предположим, что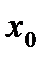 
- корень этого многочлена. Разделим 
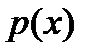на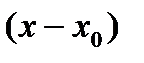 
. Тогда исходный полином можно представить в виде:
,
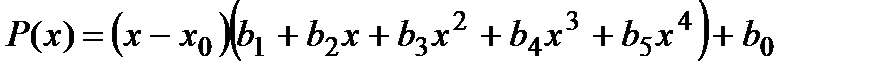где между коэффициентами a и b есть связь. Вычислим её. Раскрыв скобки, и сгруппировав известные и неизвестные величины, получим:
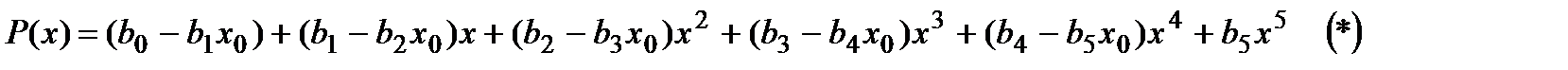
Теперь приравняем соответствующие коэффициенты a и b между собой:
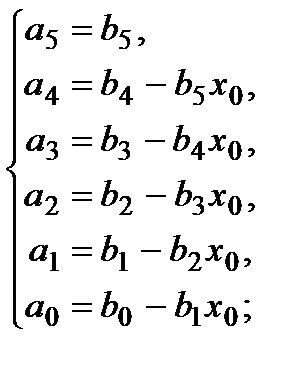
Разрешим эту систему относительно коэффициентов b:
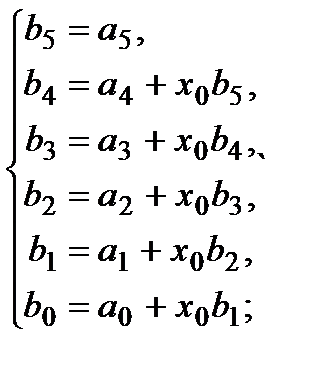
Обратите внимание, что у нас получилась явная рекуррентная последовательность: результат каждой строчки подставляется в следующую.
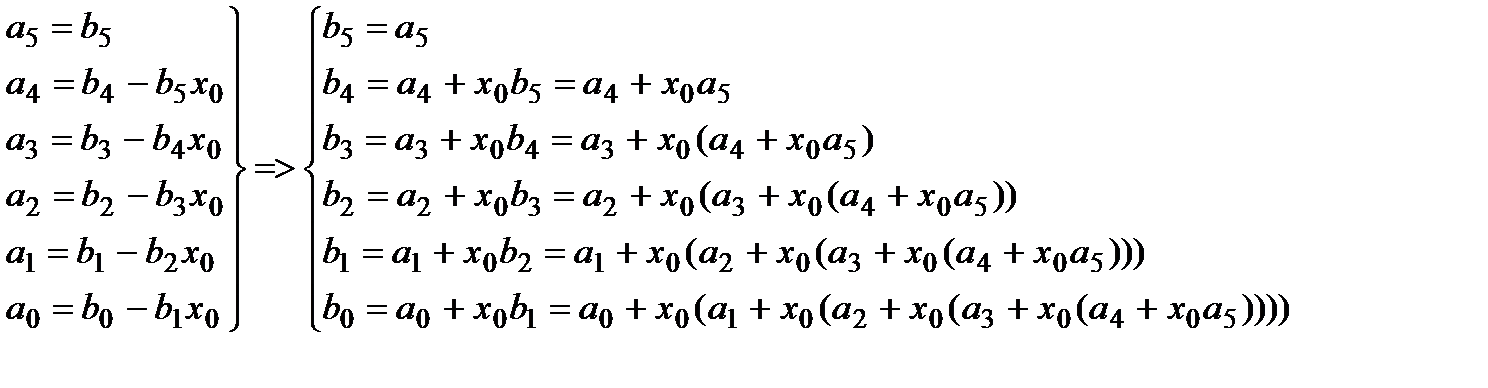
В общем виде рекуррентность выглядит так:
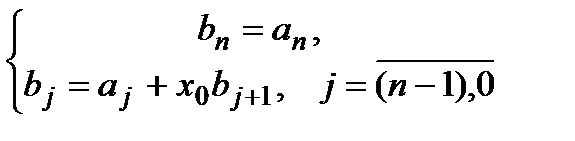
А правило Горнера в общем виде записывается так:
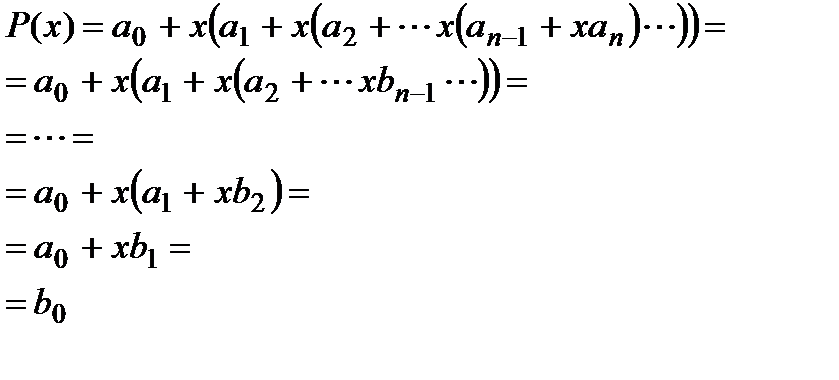
Обратите внимание, что схема Горнера не решает многочлен, а только удобно вычисляет его значения. Для решения с помощью схемы Горнера используется модифицированный метод Ньютона-Рафсона.
Дата: 2019-05-28, просмотров: 445.
