Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Согласно всем известным на сегодня и проверенным временем моделям[11] ценообразования на опционы цена опциона является функцией f ( S , X , T , σ , R_f ), которая зависит от текущей цены акции S, ударной цены опциона X, срока действия опциона T, безрисковой процентной ставки R_f и волатильности[12] акции, обозначаемой σ.

Если колл-опцион будет использован на какой-то момент в будущем, то ценность этого опциона на момент его предъявления будет определяться разницей между текущей котировкой акции и ударной ценой опциона. Для пут-опциона, наоборот – между ударной ценой и текущей котировкой. Колл-опцион становится более привлекательным по мере роста цены акции, в то время как пут-опцион становится менее привлекательным для потенциальных инвесторов и спекулянтов. Таким образом, увеличение значения S ведёт к увеличению цены колла и уменьшению цены пута. Аналогично, колл-опционы становятся менее ценными по мере уменьшения текущей цены акции, на который они выписаны, а путы – более ценными.

Волатильность акции отражает степень рискованности капиталовложений в данную акцию. Если волатильность высокая, то больше вероятности того, что владелец получит возможность использовать опцион и заработает положительный доход. Это верно как для колла так и для пута. Таким образом, чем больше волатильность акции, на которую выписан опцион тем больше цена опциона.

Более высокое значение (безрисковой) процентной ставки означает более высокую цену денег, что в свою очередь означает более высокие отдачи от капиталовложений, ожидаемые инвесторами. Это означает более высокие ожидаемые значения котировок акций в будущем, то есть значения переменной S на момент в будущем когда будет использоваться опцион (если он будет использоваться). Увеличение ожидаемого значения S ведёт к увеличению цены колла и уменьшению цены пута, и наоборот.

Срок действия опциона для американского типа однозначно положительно влияет на цену опциона: чем больше срок действия опциона, тем инвесторы спокойнее будут себя чувствовать имея в своём портфеле этот опцион. Право осуществить сделку на определённых сегодня условиях, которое будет сохранять силу в течение нескольких лет, естественно, будет иметь большую ценность, чем такое же право, которое будет действовать в течение нескольких дней. Но для европейских опционов есть один нюанс если по акциям, на который выписан рассматриваемый нами опцион, выплачиваются дивиденды. Вы прекрасно знаете, что котировка акции на любой момент времени отражает рыночную оценку того, чего корпорация-эмитент сможет для своих владельцев, то бишь акционеров, заработать за всю свою жизнь[13]. Когда выплачиваются дивиденды, акции падают как раз на сумму, равную дивидендам, поскольку эти дивиденды берутся и, поэтому, вычитаются из прибыли этой самой корпорации. Если ожидаются значительные выплаты дивидендов, то может возникнуть ситуация, когда более краткосрочный опцион будет стоить дороже, чем более долгосрочный. Таким образом, для европейского опциона нельзя однозначно сказать, что больший срок действия опциона увеличивает ценность опциона. Это будет верно только в том случае, когда дивиденды не выплачиваются.

Всё вышесказанное подытожено в следующей таблице:

 

	Европейский		Американский
	колл	пут	колл	пут
Текущая цена акции	+	-	+	-
Ударная цена опциона	-	+	-	+
Срок действия опциона	?	?	+	+
Волатильность акции	+	+	+	+
Безрисковая процентная ставка	+	-	+	-

Таблица 5.3 Факторы, влияющие на цену опциона

Опционные стратегии.

На всевозможные стратегии и позиции использующие опционы мы потратили целую пару. Вам не надо знать наизусть названия каждой стратегии, но зная структуру портфеля, о котором идет речь, Вы должны уметь построить диаграмму ожидаемой прибыли[14]. Вот некоторые из них[15]:

 

                                                   доход

 

i) длинная позиция по акции

и короткая позиция по колл-опциону

                                                       

                                                                      х          S_T

 

 

                                           

                                              

ii) короткая позиция по акции

и длинная позиция по коллу

 

iii) длинная позиция по акции

и длинная позиция по путу

 

iv) короткая позиция по акции и

короткая по путу

 

 

 

v) бычий спрэд при помощи коллов:

длинная позиция по коллу с х₁                   х₁

и короткая по коллу с х₂                                                                        х₂

 

 

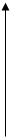бычий спрэд при помощи путов:

длинная позиция по путу с х₁

и короткая по путу с х₂

 

 

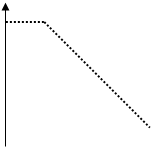медвежий спрэд при помощи коллов:

короткая позиция по коллу с х₁ и

длинная позиция по коллу с х₂

(попробуйте сами построить медвежий

спрэд при помощи путов)

 

 

vi) Батрфлай спрэд при помощи коллов:

короткие позиции по двум коллам с х₂,

длинные позиции по коллам с х₁ и х₃            х₁        х₃

(попробуйте сами построить такой спрэд         х₂

при помощи путов)

 

 

vii) Стрэдл: длинные позиции                          х

по коллу и путу с одинаковыми х

 

Паритет пута-колла.

Рассмотрим следующий портфель, который состоит из длинной позиции по акции, длинной позиции по путу и короткой по коллу. При этом все параметры обоих опционов одинаковы. При этом стоимость портфеля на момент наступления срока использования опциона будет следующей:

 

	Если S<X	Если S ≥ X
Длинная акция	S	S
Длинный пут	X-S	0
Короткий колл	0	-(S-X)
Весь портфель	X	X

 

Таким образом, рассматриваемый портфель является безрисковым (в любом случае портфель будет в итоге стоить X), то есть, чтобы определить его стоимость на сегодня мы должны дисконтировать его по безрисковой процентной ставке:

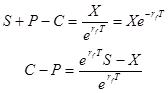Последнее уравнение показывает так называемый паритет пута-колла, согласно которому между ценой пута и соответствующего колла есть зависимость и, зная цену одного, Вы всегда сможете определить цену другого.

Если S = X, то есть когда ударная цена акции равна текущей цене акции, то получаем следующее равенство:

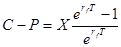Поскольку значение e^ξ всегда больше единицы при любом положительном значении ξ (а произведение r_fT у нас даёт всегда положительное число), то значение обоих частей уравнения является положительной. Это означает, что если ударная цена опциона равна текущей цене акции, то колл-опцион всегда будет стоить дороже, чем соответствующий пут.